基于结构可靠度的在役桥梁安全性评估*
2016-12-12韩振国冯莹
韩振国,冯莹
(泰州职业技术学院,江苏泰州 225300)
基于结构可靠度的在役桥梁安全性评估*
韩振国,冯莹
(泰州职业技术学院,江苏泰州 225300)
基于国内外桥梁安全性评估研究成果,结合钢筋砼桥梁的特点,研究在役钢筋砼梁桥承载工作状态评估方法,阐述了桥梁安全性评估的内涵,结合工程实例论述了基于结构可靠度理论的在役中小型钢筋砼梁桥的安全性评估方法的基本思路、优缺点和适用性。
桥梁;结构可靠度;安全性评估;优化分析
目前,在役桥梁因各种因素出现老化、破损等现象,导致桥梁结构承载安全状态不佳,由此引起的安全问题日益突出,如何正确、合理地评估在役桥梁结构的承载安全性已成为研究热点。在役桥梁结构安全性评估方法较多,在工程实践中应用较多的有基于评估规范、荷载试验、设计检算、可靠度理论、模糊理论等的方法。该文研究基于结构可靠度理论的在役钢筋砼梁桥承载工作状态评估方法。
1 结构可靠性分析原理
1.1 结构可靠性和可靠度
在役桥梁结构的可靠性是指在规定的时间和条件下完成预定功能的特性,采用结构可靠度作为度量指标。结构完成预定功能的概率称为结构的可靠概率,用Ps表示;结构未能完成预定功能的概率称为结构的失效概率,用Pf表示。两者关系可用下式表示:

式中:Z为结构工作状态函数,称为结构功能函数;R、S分别为代表能力、代表荷载的随机变量。
根据式(1),对在役桥梁结构进行可靠度分析的核心是如何根据随机变量的统计特性和结构的极限状态方程计算结构的失效概率。
1.2 结构极限状态
结构工作状态下设定一个阈值,若超过该阈值,则结构处于不安全、不耐久或不适用的状态;若没有超过该阈值,则结构处于安全、耐久、适用的状态。该阈值即为结构的极限状态。用X1,X2,…,Xn表示结构的基本随机变量,则结构功能函数可表示为Z=g(X1,X2,…,Xn),结构工作状态可用式(2)表示,图1为在直角坐标系中结构的工作状态。

对应极限状态时的方程Z=g(X1,X2,…,Xn)=0即为极限状态方程。

图1 结构工作状态示意图
1.3 结构可靠性指标
工程实践中直接应用数值积分方法计算结构失效概率较困难,多采用近似方法,即用可靠性指标β表示结构的安全指标或可靠性指数。对应功能函数Z=R-S中,假设R 和S均服从正态分布,其均值和标准差分别为μR、μS和σR、σS,则功能函数Z= R-S也服从正态分布,其均值和标准值分别为μZ,可靠性指标β可表示为:

2 结构可靠度计算方法
计算在役桥梁结构可靠度时,基于结构功能函数服从正态分布才能利用正态概率分布函数建立结构可靠指标与结构失效概率间的一一对应关系,而对于存在许多复杂问题的实际工程,可能不会是线性函数,由于是不服从正态分布的基本随机变量,其结构功能函数也不服从正态分布,这样就不能进行结构可靠性指标计算。因此,需研究实际工程中如何采用近似方法计算结构可靠度指标。结构可靠度研究初期提出采用中心点法计算结构可靠性指标,但该方法未能考虑随机变量的分布概率模型,非线性功能函数在随机变量的平均值处展开不合理,且运用相同力学含义但数学表达式不同的极限状态方法求得的结构可靠性指标不同。后续研究中采用验算点方法(JC法),即在考虑随机变量分布概率模型的情况下,通过“当量正态化”把非正态变量化为当量正态变量,在计算工作量不增多的条件下,以较高的精度近似计算可靠指标β,求得满足极限状态方程的“验算点”设计值。图2为在役桥梁使用JC法迭代计算可靠性指标β的流程。

图2 JC法计算可靠度指标的流程
JC法能给出固定的求解步骤,其计算方法和过程通俗易懂,计算速度快,在计算量增加不多的条件下能对随机变量为任意分布状态下的结构可靠性指标β进行较高精度的近似计算,计算精度能满足工程实际需要,且适合编制计算程序和便于一般工程技术人员应用,因而成为结构可靠度计算方法中使用率较高的方法之一。
3 计算模型及算例
计算在役桥梁结构可靠度时需采用其结构功能函数,即在规定的继续使用期内,在正常使用、维护条件下,参考外部环境和结构自身抗力衰减等影响因素,服役某一时刻后的桥梁结构在后续服役期内完成预定功能的函数,表达式如下:
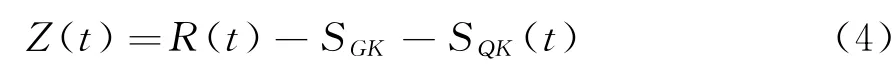
式中:Z(t)为极限状态随机过程;R(t)为结构抗力随机过程;SGK为结构恒载效应随机过程;SQK(t)为结构效应随机过程。
考虑材料老化、环境不利、超载行车等因素造成的结构承载力下降及现役桥梁实际运营中荷载效应的变化,按照不同基准期下抗力最小值和荷载效应最大值的原则,采用JC法进行“当量正态化”,计算结构抗力与荷载效应的均值和标准差,采用改进的一次二阶矩法计算现役桥梁的时变可靠指标β(t),表达式如下:
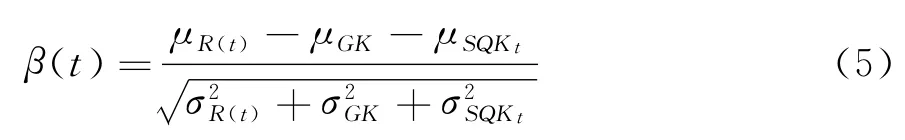
式中:μR(t)、σR(t)分别为结构抗力的平均值与方差;μGK、σGK分别为恒载效应的平均值与方差;μSQKt、σSQKt分别为活载效应的平均值与方差。
下面以某在役桥梁为例阐述运用JC法求解在役桥梁可靠性指标β(t)的过程。该桥全长138 m,跨径布置为(18+23+25+25+23+24)m,桥面宽度为净7 m+2×1.0 m。上部结构采用钢筋砼T形梁,下部结构采用重力式墩与框架式墩、桩基础。该桥建成于1980年,设计荷载为汽-20级。评估检查时间为2015年,检测结论如下:1)桥面铺装损坏严重,伸缩缝破损、脱落、淤填等;桥面横坡、纵坡顺适,排水效果良好;栏杆断裂且钢筋锈蚀严重。2)主梁底面有大量裂缝,结构表面有剥落、露筋现象。3)桥墩有被撞击损伤痕迹,尤其是通航主跨的框架式桥墩。4)梁体存在大量明显裂缝,尤其是边梁裂缝较多,裂缝宽度为0.05~0.30 mm,超过规范规定的最大裂缝宽度限值,且在试验荷载作用下主梁控
制断面裂缝存在扩展趋势。
借助MATLAB编程计算该桥承载力、刚度及安全评估参数随服役时间增长的变化,计算结果见表1、表2。
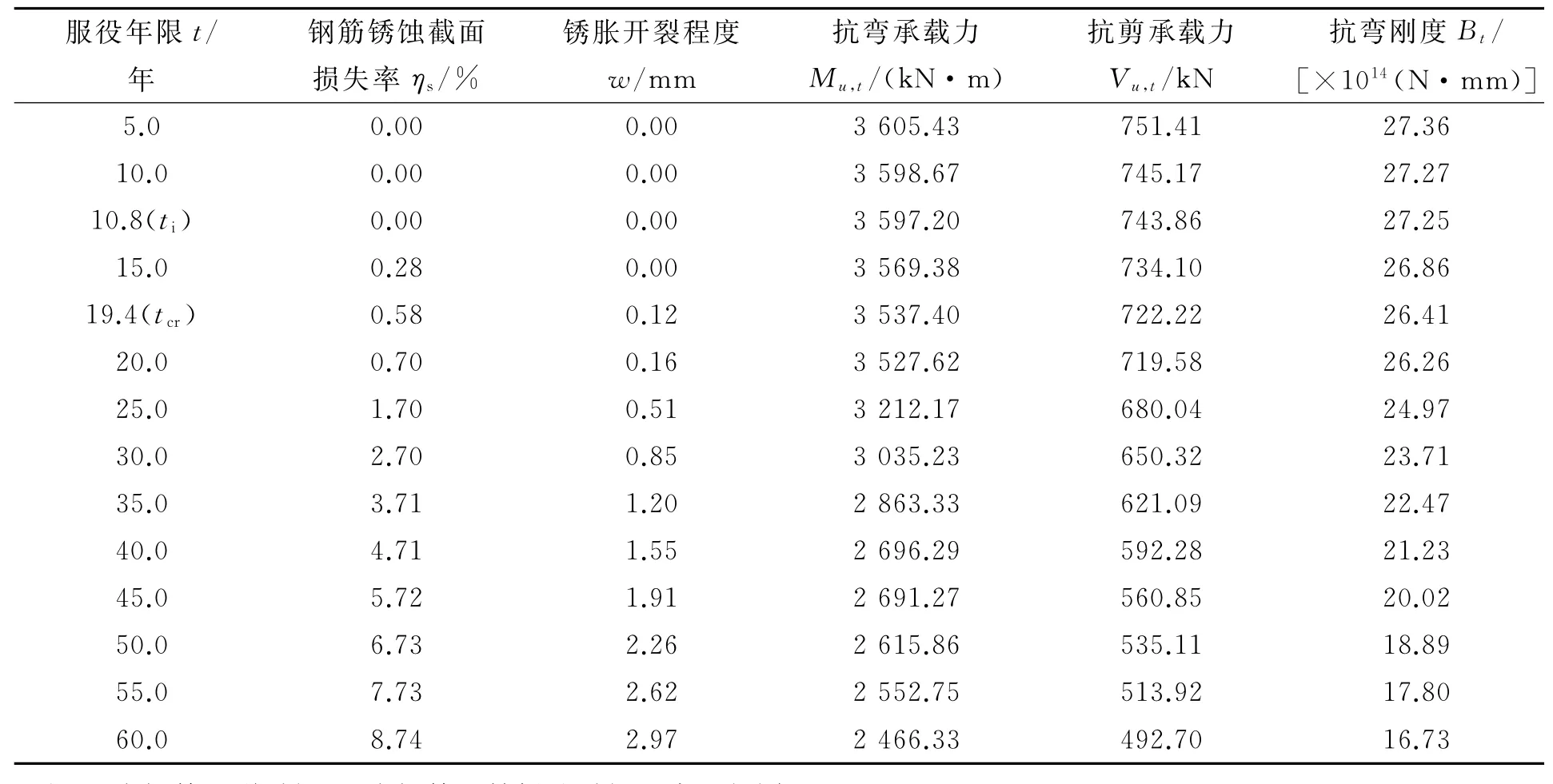
表1 某在役桥梁时变承载状态计算结果

表2 某在役桥梁时变评估参数计算结果
由表1、表2可以看出:该桥抗弯承载力降低系数ζM、抗剪承载力降低系数ζV及抗弯刚度降低系数ζB随着结构时变可靠性指标β的下降而减小,锈胀开裂程度系数ζw随着β的下降而增大,反映出该桥承载安全状况衰变的程度,表明其结构承载安全性在逐步下降。也说明上述方法对在役桥梁结构的安全性评估既合理有效,又实用可行。
4 结语
综上所述,基于结构可靠度理论的评估方法是一种有效的评估结构安全性的手段,它从结构概率安全性角度出发,考虑桥梁结构抗力和荷载随时间变化的不确定性并将其视为随机过程来评估桥梁结构的可靠性,为桥梁安全性评估提供了一个合理的理论框架。该方法借助现场检测数据通过可靠度理论计算进行评估,理论较完善,可处理荷载和抗力的不定性(尤其是这些不确定性对结构可靠度的影响),因而适用于有历史数据记录的桥梁评估。借助于日益完善的在役桥梁结构数据信息,在实际桥梁加固维修时,运用该方法进行优化分析确定达到容许的安全等级条件,从而对有限的养护资金进行合理分配,取得良好的维修养护效果。
[1] 路杨,于利存.基于动态环境因素的桥梁运营安全风险评估研究[J].筑路机械与施工机械化,2013(7).
[2] 黄志伟,黄侨,任远.基于程度分析的中小桥梁评估方法[J].东南大学学报:自然科学版,2012,42(2).
[3] 司奎,史家钧.基于可靠性的桥梁评估方法[J].山西建筑,2005,31(5).
[4] JTG D60-2015,公路桥涵设计通用规范[S].
U447
A
1671-2668(2016)06-0159-03
2016-07-05
泰州职业技术学院2016年度科研项目(TZYKY-16-17)
