深层排水管布设方式对土质路堑边坡稳定性的影响

2016-12-12吕军

公路与汽运 2016年6期

关键词：排水管深层倾角

吕军

（湖南省永龙高速公路建设开发有限公司，湖南永顺 416700）

深层排水管布设方式对土质路堑边坡稳定性的影响

吕军

（湖南省永龙高速公路建设开发有限公司，湖南永顺 416700）

以永龙（永顺—龙山）高速公路K23+348—575土质路堑边坡为例，采用数值模拟方法对深层排水管的布设方式进行研究，分析不同排水管倾角及不同布设长度对地下水位线、孔隙水压力及边坡稳定性的影响。结果表明，边坡地下水位线高度随着深层排水管的倾角增加而增加，孔隙水压力和边坡稳定性随着深层排水管倾角的增加而减小；在采用最佳角度布设深层排水管时，采用上层排水管长度较短而下层排水管较长的方式更有利于边坡排水。

公路；深层排水管；土质边坡；边坡稳定性；地下水

众多研究表明，边坡内部地下水位较高是造成边坡失稳的主要原因之一。夏开宗等认为地下水对边坡的作用主要为潜在滑动面的扬压力及动水压力，并且与岩层面的倾角有关；宋波等提出地下水位上升后边坡底部有效应力明显减小，对边坡稳定性极为不利。因此，对边坡进行有效排水，进而降低地下水位是保证边坡安全的必要手段。目前工程中常用的方法有深层排水管排水、虹吸排水等，其中深层排水管法应用最广泛。

现有针对排水管的研究大多从其对边坡内部渗流场的影响角度进行数值分析，如叶冬冬等模拟了水位骤降条件下有无排水孔时的边坡渗流场分布；张世华等利用MATLAB对虹吸排水后的地下水浸润线分布进行分析，确定了最佳虹吸排水孔位置。但以上研究并未对深层排水管的不同布设角度及布设长度进行详细探究。为此，该文以永龙（永顺—龙山）高速公路土质路堑边坡为例，采用有限元方法对不同深层排水管布设角度与长度下边坡内部地下水位线位置、孔隙水压力和边坡稳定性进行计算分析，为工程实践提供参考。

1 非饱和渗流有限元计算理论

根据达西定律推导出土体内非恒定渗流偏微分方程为：

式中：Kx、Ky分别为x 和y 方向的渗透系数；H为渗流介质中的总水头；Q为源汇项；γw为水的重度；mw为单位贮水量；t为时间。

土体非恒定渗流有限元方程为：

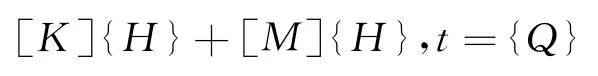
式中：［K］为单元特征矩阵；H｛｝为恒定流节点水头向量；［M］为单元质量矩阵；｛H｝，t为非恒定流节点水头向量；Q｛｝为节点流量向量。

2 工程概况与模型建立

2.1 工程概况

选用永龙高速公路K23+348-575左侧土质路堑高边坡进行分析。该段边坡由粉质黏土、全风化砂质板岩组成，结构较松散，强度差，易冲刷流失，雨水浸润易滑塌、剥落，边坡稳定性较差。其土质参数见表1。

表1 边坡的土质参数

在大气降雨（尤其是突发性大暴雨）作用下，孔隙水压力增大，边坡自重增加，易产生沿岩土界面的滑动变形或土层内部的圆弧形滑动变形。该地区地下水主要为基岩裂隙水，赋存于砂质板岩的风化、节理裂隙中，但裂隙多泥质充填，连通性较差，赋水条

件一般，主要接受大气降水补给，以沿裂隙渗流形式或受地形切割排出地表，山体斜坡部位受地形影响，地下水补给、排泄快，钻孔揭露地下水最大埋深约20 m。

该边坡共分为四级，每级高10 m，坡比分别为1∶0.75、1∶1、1∶1、1∶1.25，每级平台均设置截水沟；边坡坡脚设置边沟；左侧一、二级边坡分别设置2排深层排水管，呈梅花形布置，水平间距8 m，垂直间距3 m，斜孔深12 m，孔径φ120 mm，孔内放置φ100 mm PVC管。

2.2 计算模型

采用岩土工程专用有限元软件SEEP／W和SLOPE／W，根据实际工程建立有限元模型（见图1）。为同时考虑计算精度与计算效率，设定四边形网格尺寸为1 m×1 m。在边坡左侧边界处设定20 m为总水头，边坡坡面为自由渗出边界，边坡底部为不透水边界，通过稳态计算得到边坡内部初始地下水位线位置（见图2）。根据工程经验，稳定状态下深层排水管中无孔隙水压力，故设定排水管为零孔隙水压力边界。采用Ordinary法对边坡初始状态进行稳定性分析，得到最危险滑动面（见图2），此时边坡安全系数为1.21，后续分析中采用该滑动面进行稳定性对比分析。

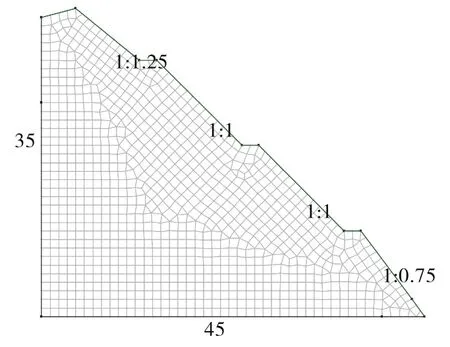
图1 边坡有限元网格划分（单位：m）

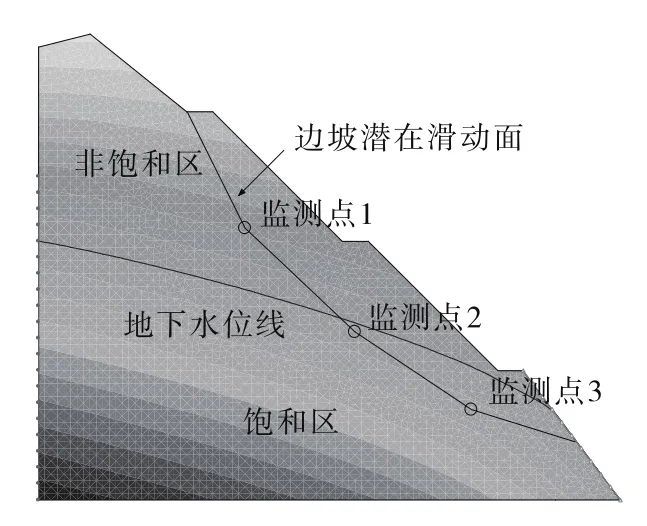
图2 边坡初始地下水位线与潜在滑动面

3 计算结果分析

3.1 深层排水管倾角对边坡稳定性的影响

采用有限元方法计算分析不同深层排水管布设倾角（见表2）对排水效果的影响，结果见图3。

表2 不同角度深层排水管设计方案

图3 不同角度排水管布设方案下边坡内部地下水位线位置

从图3可看出：采用相同长度排水管情况下，排水管倾角设置为3°时，地下水位线完全处于潜在滑动面下方；倾角为10°时，地下水位线略有上升，但仍处于边坡潜在滑动面下方；倾角为20°时，地下水位线上升至接近潜在滑动面处；倾角达到30°时，地下水位线开始与潜在滑动面相交，可认为此时深层排水管已不能满足排出边坡内部水分的要求。说明当深层排水管长度相同时，其倾角越小排水能力越好，倾角越大其排水能力越差。这是由于边坡地下水位线位置往往呈内部较高、向边坡外部方向越来越低的趋势（见图2），当深层排水管倾角较小时，可有效深入地下水位线内部，排出地下水；而倾角设置过大时，其与地下水位线的关系接近平行，不能深入边坡内部饱和区，无法有效发挥排水作用。

根据已有研究成果，边坡内部地下水所造成的潜在滑动面处的孔隙水压力上升是导致边坡失稳的主要原因之一，有必要进一步分析排水管布设对滑动面处孔隙水压力的影响。潜在滑动面上3个监测点处的孔隙水压力随排水管倾角的变化见图4。

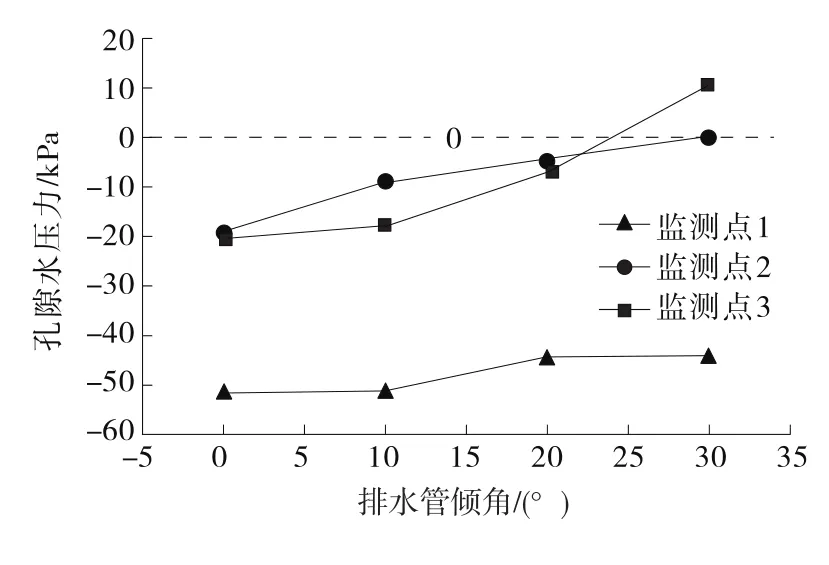
图4 孔隙水压力与排水管角度的关系

从图4可看出：由于监测点1处位置较高，其孔隙水压力始终保持在负值，随着排水管倾角的增加，其孔隙水压力逐渐上升；监测点2处的孔隙水压力也随着排水管倾角的增加而增加，但并未产生正孔隙水压力；对于接近坡脚处的监测点3，当排水管倾角处于3°、10°、20°时，其孔隙水压力小于零，但当排水管倾角达到30°时，坡脚处出现正孔隙水压力，此时作用在土体上的有效应力相应减小，导致坡脚处的滑动面抗剪强度降低，容易产生边坡失稳。

基于以上孔隙水压力分析，采用Mogenstern-Price、Ordinary和Bishop 3种常用边坡安全系数计算方法对不同排水管倾角下边坡的稳定性进行计算，结果见图5。

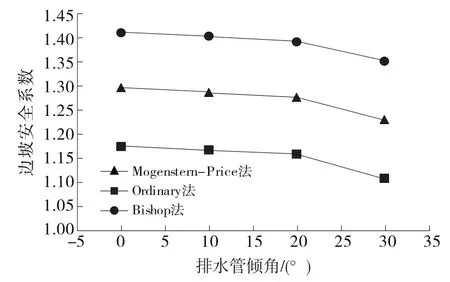
图5 不同排水管倾角对边坡安全系数的影响

从图5可看出：无论采用何种计算方法，当排水管倾角为3°时，边坡安全系数都最大；随着排水管角度的增大，边坡安全系数逐渐减小，倾角达到30°时边坡安全系数最小。Ordinary法计算所得边坡安全系数比实际值偏小，可看作具有一定的安全储备；但当排水管倾角为30°时，Ordinary法计算所得安全系数小于1.3，可认为存在一定的失稳风险。

3.2 深层排水管长度对边坡稳定性的影响

为进一步探讨排水管长度变化对边坡排水性能及边坡稳定性的影响，设计方案5、方案6（见表3）与方案1～4进行对比分析，结果见图6。

表3 不同长度排水管布设方案

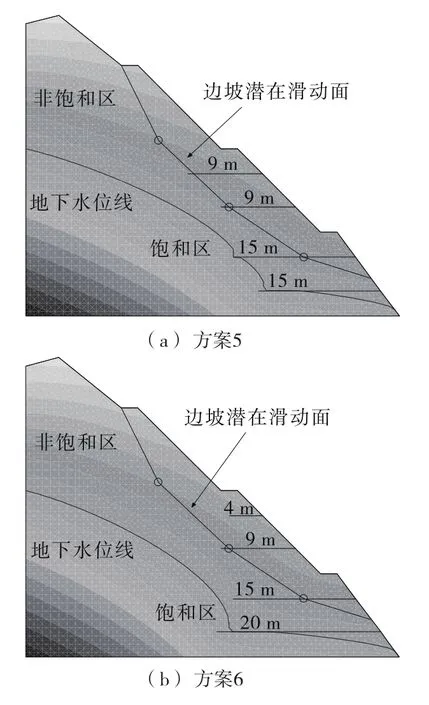
图6 不同长度排水管布设方案下边坡内部地下水位线位置

从图6可看出：当排水管布设长度并非均匀分布时，排水效果与均匀分布有着明显区别。方案5的地下水位线位置与方案1相差不多，略有下降；方案6的地下水位线位置与方案1与方案5相比明显下降，远低于潜在滑动面位置。说明排水管的布设长度会对边坡内部水位产生明显影响，底部排水管越长，排水效果越好。产生这种现象的原因主要是边坡底部饱和区域较大，且靠近坡面，增加底部排水管长度，排水效果明显增强；而边坡上部地下水位线较深，距坡面较远，排水管并未深入饱和区，上部排水管长度对排水效果的影响不明显。

不同长度排水管布设方案下各监测点的孔隙水压力见表4，边坡安全系数见表5。