物理模型中膨胀岩相似材料湿度迁移规律研究
2016-12-12王军辉张新
王军辉,张新
(1.长沙理工大学,湖南长沙 410004;2.江西嘉圆房地产开发有限责任公司,江西南昌 330003)
物理模型中膨胀岩相似材料湿度迁移规律研究
王军辉1,2,张新2
(1.长沙理工大学,湖南长沙 410004;2.江西嘉圆房地产开发有限责任公司,江西南昌 330003)
在研究不同初始含水率、不同密度膨胀岩巷道围岩湿度场时,需在相似材料配比的基础上进行物理模型试验,模型填筑后的一段时间内填筑材料的含水率会受重力影响发生变化,模拟施工用水及其他水分时实测的围岩含水率实际上是在重力影响下已发生变化的含水率,并不能精确反映施工用水对巷道围岩的影响。文中通过对不同密度、不同含水率膨胀岩配比材料进行水分迁移试验,得出了物理模型内部含水率随时间的分布规律,为解决膨胀岩湿度场问题奠定基础。
公路;膨胀岩;重力势;含水率;密度;模型试验
对于膨胀岩巷道围岩湿度场的研究,围岩内部水分的测定尤为重要,关系到围岩膨胀力的大小,是围岩膨胀应力计算的基础。而膨胀岩这种似岩非岩、似土非土且对水敏感的软岩吸水膨胀、失水收缩的特性,对含水率的精度要求更高。对膨胀岩巷道围岩湿度场常采用物理模型试验的方式进行研究,通过相似材料的配比试验得到理想的配比,通过配比按照相似模型的比例填筑模型。模型筑好需稳定一段时间再进行巷道开挖及模拟,此时正是重力势对模型内含水率的作用时段。为此,该文针对90 cm×90 cm×30 cm模型进行不同密度、不同初始含水率下膨胀岩配比材料试验研究,探讨重力作用下的水分迁移规律。
1 试验设计
1.1 试验材料及方案
在室内进行相似材料配比,其中:砂胶比为1∶1;石膏∶膨润土及高岭土=1∶1,膨润土∶高岭土=5∶2,淀粉1.5%。采用壁厚2 mm、内径4.7 mm的长度为90 cm的PVC管进行材料填装,两端用塑料布密封后在底部留一小孔,保证水分能畅通。考虑3种初始含水率、3种密度的膨胀岩配比材料,共进行10组试验(见表1)。
膨胀岩的基本指标:自由膨胀率为103.3%;干燥饱和吸水率为52.3%;极限膨胀量为31.2%;单轴抗压强度为0.535 MPa。
1.2 试验过程(见图1)
试验前按照PVC管的体积与密度计算材料用量,配制不同初始含水率的膨胀岩材料,材料配好后
充分浸润12 h后进行填装,填装前测定2个初始含水率(取平均值)。取90 cm PVC管一段密封后按每层5 cm的高度用量进行填充,用自制夯实管进行分层击实,通过质量和体积控制方法控制密度,填充完后直立静置48、72、96、120 h。用割管锯沿纵向锯开,沿管纵向距管顶10、30、45、60、80 cm处取芯,用烘箱烘干测定含水率。

表1 试验方案

图1 试验过程
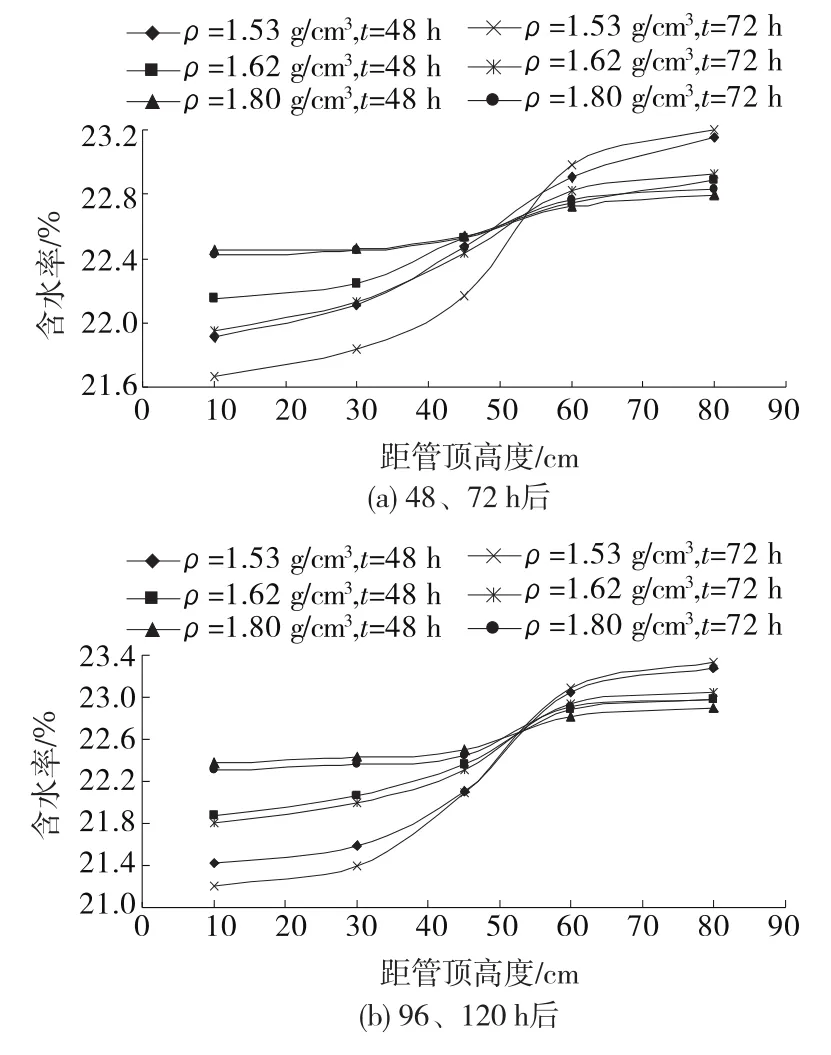
图2 含水率为22.65%的膨胀岩材料在静置不同时间后的含水率分布
2 试验结果分析与应用
2.1 试验结果分析
通过试验,得到不同初始含水率、不同密度下膨胀岩配比材料在竖向高度的水分变化规律。图2为初始含水率为22.65%的膨胀岩材料在静置不同时间后的含水率分布。从图2可看出:初始含水率为22.65%的膨胀岩材料在静置不同时间后不同高度处的含水率呈现微小变化,在中心靠下的上部水分减小,下部水分增大,但变化值很小。在48 h后,密度为1.53 g/cm3的材料其含水率最大减小值(距管顶部10 cm处)为0.74%,最大增大值(距管底部10 cm处)为0.5%;密度为1.8 g/cm3的材料最大减小值为0.18%,最大增大值为0.14%;密度值为1.62 g/cm3的材料介于上述两种材料之间,最大减小值为0.5%,最大增大值为0.24%。在72 h后,呈现上部含水率继续减小、下部含水率继续增大的趋势,密度为1.53 g/cm3的材料最大减小值为0.98%,最大增大值为0.55%;密度为1.8 g/cm3的材料最大减小值为0.23%,最大增大值为0.18%;密度为1.62 g/cm3的材料最大减小值为0.7%,最大增大值为0.28%。在96 h后,密度为1.53 g/cm3的材料最大减小值为1.23%,最大增大值为0.63%;密度为1.8 g/cm3的材料最大减小值为0.27%,最大增大值为0.25%;密度值为1.62 g/cm3的材料最大减小值为0.78%,最大增大值为0.33%。在120 h后,密度为1.53 g/cm3的材料最大减小值为1.44%,最大增大值为0.68%;密度为1.8 g/cm3的材料最大减小值为0.34%,最大增大值为0.33%;密度为1.62 g/cm3的材料最大减小值为0.84%,最大增大值为0.39%。可通过插值的方式得出该含水率下其他密度材料静置48、72、96、120 h后的含水率变化曲线。

图3 含水率为19.21%的膨胀岩材料在静置不同时间后的含水率分布
图3 为初始含水率为19.21%的膨胀岩材料在静置不同时间后的含水率分布。从图3可看出:初始含水率为19.21%的膨胀岩材料在静置不同时间后不同高度处的含水率变化趋势仍旧是中心左右位置以上的含水率减小、下部含水率增大,减小和增大幅度比初始含水率为22.65%的材料稍小。在48 h后,密度为1.53 g/cm3的材料其含水率最大减小值为0.54%,最大增大值为0.48%;密度为1.8 g/cm3的材料最大减小值为0.3%,最大增大值为0.29%;
密度为1.62 g/cm3的材料最大减小值为0.47%,最大增大值为0.31%。在72 h后,密度为1.53 g/cm3的材料最大减小值为0.63%,最大增大值为0.57%;密度为1.8 g/cm3的材料最大减小值为0.36%,最大增大值为0.32%;密度为1.62 g/cm3的材料最大减小值为0.55%,最大增大值为0.38%。在96 h后,密度为1.53 g/cm3的材料最大减小值为0.75%,最大增大值为0.6%;密度为1.8 g/cm3的材料最大减小值为0.45%,最大增大值为0.44%;密度为1.62 g/cm3的材料最大减小值为0.67%,最大增大值为0.47%。在120 h后,密度为1.53 g/cm3的材料最大减小值为0.88%,最大增大值为0.72%;密度为1.8 g/cm3的材料最大减小值为0.3%,最大增大值为0.29%;密度为1.62 g/cm3的材料最大减小值为0.53%,最大增大值为0.48%。可通过插值的方式得出该含水率下其他密度材料静置48、72、96、120 h后的含水率变化曲线。
图4为初始含水率为16.3%的膨胀岩材料在静置不同时间后的含水率分布。从图4可以看出:初始含水率为16.3%的膨胀岩材料在静置不同时间后不同高度处的含水率变化趋势仍旧是中心左右位置以上含水率减小、下部含水率增大。在48 h后,密度为1.53 g/cm3的材料其含水率最大减小值为0.34%,最大增大值为0.33%;密度为1.8 g/cm3的材料最大减小值为0.15%,最大增大值为0.18%;密度值为1.62 g/cm3的材料最大减小值为0.23%,最大增大值为0.27%。在72 h后,密度为1.53 g/cm3的材料最大减小值为0.48%,最大增大值为0.41%;密度为1.8 g/cm3的材料最大减小值为0.19%,最大增大值为0.20%;密度值为1.62 g/cm3的材料最大减小值为0.35%,最大增大值为0.33%。在96 h后,密度为1.53 g/cm3的材料最大减小值为0.55%,最大增大值为0.44%;密度为1.8 g/cm3的材料最大减小值为0.25%,最大增大值为0.24%;密度值为1.62 g/cm3的材料最大减小值为0.41%,最大增大值为0.37%。在120 h后,密度为1.53 g/cm3的材料最大减小值为0.61%,最大增大值为0.46%;密度为1.8 g/cm3的材料最大减小值为0.3%,最大增大值为0.29%;密度值为1.62 g/cm3的材料最大减小值为0.27%,最大增大值为0.30%。可通过插值的方式得出该含水率下其他密度材料静置48、72、96、120 h后的含水率变化曲线。
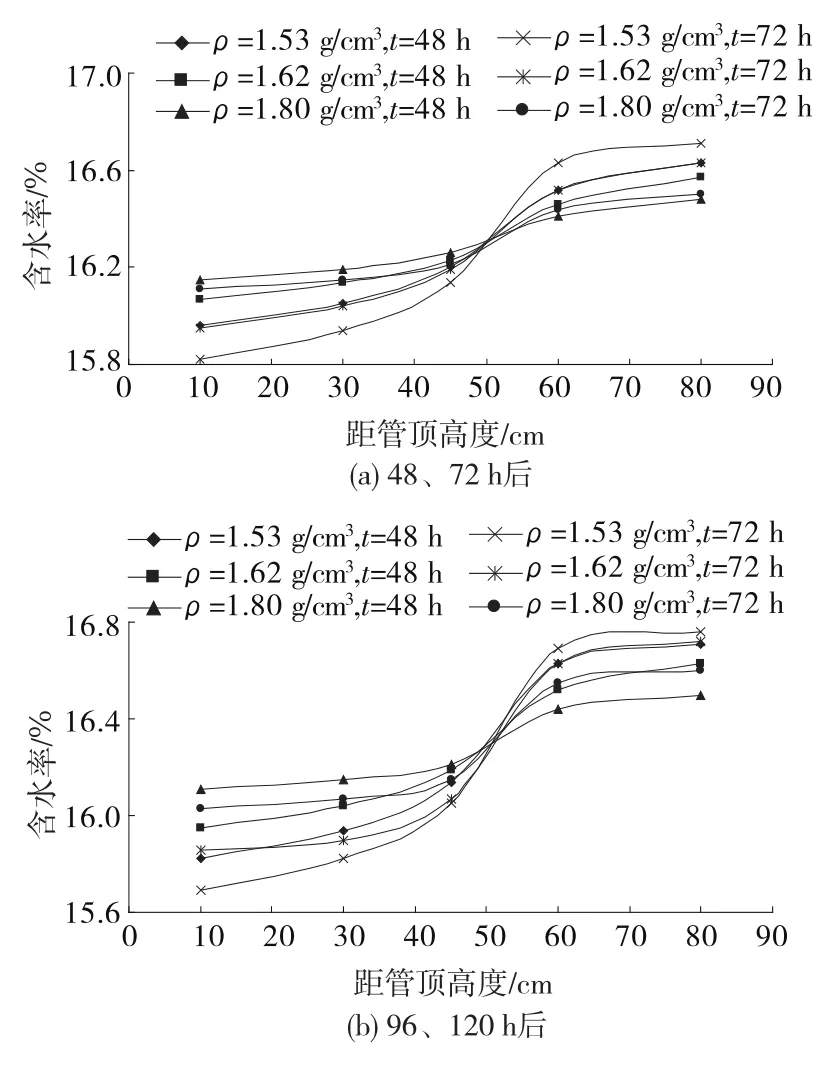
图4 含水率为16.3%的膨胀岩材料在静置不同时间后的含水率分布
图5 为初始含水率为12%的膨胀岩材料在静置120 h后的含水率分布。从图5可以看出:初始含水率为12%的膨胀岩材料在静置120 h后不同高度处的含水率基本为一条曲线,可以认为在12%含水率的重力势作用下,没有水分迁移的影响。故在后期模型上初始含水率可看作稳定值。
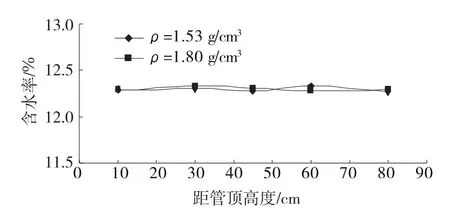
图5 含水率为12%的膨胀岩材料在静置120 h后的含水率分布
综上所述,膨胀岩材料含水率的变化和其密度及初始含水率相关,但重力势作用下的水分变化很小。从密度上考虑,密度1.8 g/cm3时水分变化最小,密度为1.53 g/cm3时水分变化稍大,密度为1.62 g/cm3时含水率变化介于两者之间。从含水率上考虑,密度一定时,初始含水率高的变化值比含水率低的大。从试验效果上看,初始含水率为22.65%的试样下部有水分流失现象,初始含水率为12%的试样含水率几乎不变。
2.2 试验结果应用
水分的迁移规律很复杂,由于试验条件和时间的关系,仅从简单的几个点去分析模型中的水分变化其精度有限,但还是能通过试验得出模型中任意初始含水率、密度在任意时间点和模型部位的含水率。在利用模型来研究水分变化规律时,可通过插值的方式得出相应曲线,从而确定任意点在具体时间上的含水率值,为后续试验数据测量奠定基础。例如要得出密度为1.7 g/cm3、模型初始含水率为17%、距离管顶40 cm处48 h的含水率,可通过上述1.8与1.62 g/cm3材料在48 h后的含水率变化曲线插值得出ρ=1.7 g/cm3材料含水率变化曲线,然后通过w=16.3%与w=19.21%各部位的值插值得出w=17%的各点值,从而得到其含水率变化曲线(见图6),从图6中可找出40 cm处的含水率值。若要得出60 h的含水率,只要再进行一次插值,即将48 h的数据与72 h的数据进行插值得出60 h的值。通过这种方法可更加精确地确定后期模型中进行水分湿度场研究的初始值。

图6 密度为1.7 g/cm3膨胀岩材料静置48 h后的含水率变化曲线
3 结论
(1)室内物理模型中膨胀岩相似材料在重力势作用下水分会向下发生较小的迁移,初始含水率高的材料的水分迁移比初始含水率低的明显,初始含水率在12%以下的材料其水分基本保持不变;初始含水率的影响程度比密度高,相同含水率下,低密度材料的水分迁移比高密度明显。
(2)水分的迁移规律很复杂,通过一定的试验,用插值的方法能计算出模型中任意初始含水率和密度材料在任意时间点和模型部位的含水率大小,使后期巷道围岩在各工况下监测湿度场更加准确,在湿度场研究中具有一定的指导意义。
[1] 缪协兴,杨成永,陈至达.膨胀岩体中的湿度应力场理论[J].岩土力学,1993,14(4).
[2] 卢义玉,侯吉峰,尤祎,等.湿度应力场作用下煤矿穿膨胀岩钻孔缩径规律研究[J].采矿与安全工程学报,2014,31(3).
[3] 范秋雁.膨胀岩与工程[M].北京:科学出版社,2008.
[4] 付平勇.膨胀岩中巷道围岩湿度场相似材料模型试验研究[D].南昌:华东交通大学,2013.
[5] 董超.水分迁移对路基性状影响的研究[D].南昌:华东交通大学,2013.
[6] 缪协兴.用湿度应力场理论分析膨胀岩巷道围岩变形[J].中国矿业大学学报,1995,24(1).
U416.1
A
1671-2668(2016)06-0087-04
2016-03-31
