岩石强度准则评价方法研究

阮成瑞，李文凯

（1.河南中州路桥建设有限公司，河南周口 466000；2.河南交院工程技术有限公司，河南郑州 450046）

岩石强度准则评价方法研究

阮成瑞1，李文凯2

（1.河南中州路桥建设有限公司，河南周口 466000；2.河南交院工程技术有限公司，河南郑州 450046）

利用6种岩石强度实验数据评价4种常规三轴强度准则的适用性，以拟合偏差绝对值之和最小来拟合4种强度准则中的待定参数。结果表明，含有3个参数的指数强度准则、广义Hoek-Brown强度准则能描述多种岩石在不同围压下的强度特征，比含有2个待定参数的Hoek-Brown强度准则和Coulomb强度准则更具有适用性；从拟合偏差绝对值之和最小分析，Hoek-Brown准则优于Coulomb准则；对于多数岩石，从预测偏差角度分析，广义Hoek-Brown强度准则优于指数强度准则。

公路；岩石强度；Coulomb强度准则；Hoek-Brown强度准则；广义Hoek-Brown强度准则；指数强度准则

在实验室往往只能对几类特殊应力状态下的岩石强度进行评价，如单轴压缩强度、部分围压下压缩强度、巴西劈裂强度等，因而从理论上给出强度准则来描述各种岩石的强度特征尤为重要。常用的强度准则有直线形强度准则、Hoek-Brown强度准则、指数强度准则、广义Hoek-Brown强度准则等。虽然这些强度准则已经在不同领域得到广泛推广，但其适用性及适用范围仍有待评价分析，否则以此设计的结构工程会存在风险。

就岩石材料或水泥砼试块而言，只存在剪切和拉伸2种破坏形式。针对实验室岩石试件承受拉应力破坏的特征，由于实验操作困难及实验数据的离散性，尚缺乏明确结论；岩石试块承受压应力而破坏的实验和理论研究已广泛推广；而各种数据处理软件的出现，使得不同形式强度准则的评价分析更为科学、方便。

由于岩石真三轴应力状态下的实验做得较少，且实验数据往往离散性较大，在忽略中间主应力的情况下强度准则是趋于安全的。在现实工程中，除在研究孔壁崩落时确定地应力用到岩石真三轴强度实验外，岩体工程结构设计研究的通常是常规三轴强度实验。该文研究4种常用强度准则各待定参数的确定方式，利用4种强度准则拟合相关文献中的Westerly花岗岩、Mizuho粗面岩、Dunham白云岩、平顶山砂岩、锦屏砂岩、Yamaguchi大理岩的实验数据，评价强度准则的适用性。

1 强度准则的数学形式

Coulomb强度准则评价的物理背景是岩石破坏时具有粘结性和摩擦特性，试样的轴向抗压强度σs与围压σ3成线性关系：

式中：Q为单轴压缩强度；K为围压对强度的影响系数。

但岩石的矿物组成是非均质的，试样在破坏面上不会同时达到极限破坏强度，故实际实验数据并不是线性关系。

Hoek-Brown强度准则是抛物线，其对称轴只是与σs=σ3平行，即：

式中：m为材料的参数；σc为岩石单轴抗压强度。

把Hoek-Brown强度准则推广成完整的广义Hoek-Brown强度准则：

当参数n=1时简化成为Coulomb准则，在n =1／2时则为Hoek-Brown强度准则。

基于组成岩石矿物成分的非均质性及粘结、摩擦力在局部范围内不能同时存在的理论，随着岩石内部最小主应力的增加，岩石内部最大剪切力或主应力差趋于常数，构成如下指数强度准则：

为了加快农产品电商产业发展，当地政府部门应该高度重视基础设施建设，进一步构建完善的交通、网络等基础设施。地方政府部门也需要积极探索全新的市场化运营模式，全面调动道路工程部门、通讯部门以及各类主体，全面参与到电商产业建设当中，从而进一步实现村村通和村级网络宽带覆盖。同时还应该进一步加强农村信息服务站点建设，鼓励基层地区的邮政站、供销合作社率先改造成农村电商服务点，通过进一步提高信息服务质量、服务水平，为农产品电商发展铺平道路。

式中：Q∞为极限主应力差；Q0为单轴压缩强度；K0为围压为零时对强度的影响系数。

2 强度准则参数确定

通过不同围压下试样的强度确定各强度准则参数，而岩石在不同围压时的强度只能在试件破坏时才能得到，不同围压下岩石破坏的实验数据需要不同的试样。由于岩石试样之间的差异及组成岩石矿物的非均质性，同时破坏强度的差异并非全是由围压引起，对此需要有足够的认识。

用以评价岩石强度准则的实验数据从现有文献中引用，如文献［10］等，其中部分数据如Dunham白云岩和Mizuho粗面岩则从Mogi K.原始数据中查到，已广泛用于强度准则评价。

2.1 拟合目标的选取

确定上述4种岩石强度准则参数的常见方法有以下3种：1）线性回归法；2）最小偏差绝对值和δ1=∑|σs-f（σ3）|最小；3）最小偏差平方和δ2=∑［σs-f（σ3）］2最小。

以偏差绝对值之和δ1最小为目标搜索拟合曲线，不同围压下岩石强度理论值跟实验值最接近，即当拟合偏差mf最小时，确定不同强度准则中的待定参数。

随着各种数据处理软件的开发，以偏差绝对值之和δ1最小确定待定参数在数学上更为方便。如对于广义Hoek-Brown准则，在给定指数n后搜索参数m、δc，最后确定n。6种岩石强度平均拟合偏差mf的计算结果见表1。

表14 种强度准则对6种岩石强度的平均拟合偏差mf

2.2 4种强度准则参数确定

表2 以最小偏差绝对值之和为拟合目标确定的4种强度准则参数

3 4种强度准则评价

从以下三方面对4种岩石强度准则的适用性进行评价：1）不同强度准则对同一组岩石实验数据拟合偏差mf的比较；2）不同强度准则对同一组岩石实验数据删除2组高围压数据后拟合结果的差异；3）删除2组高围压数据后拟合曲线对该实验数据的预测性。

3.1 拟合偏差的比较

对于6种岩石常规三轴压缩实验结果，分别运用4种强度准则进行拟合，以拟合偏差绝对值之和最小确定强度准则中的待定参数。表1、表2为实验数据的平均拟合偏差和相应强度准则参数。为了方便分析，通过绘制柱状图来确定4种强度准则对同一岩石实验数据的平均拟合偏差关系（见图1）。

由图1可知：含3个参数的广义Hoek-Brown强度准则、指数强度准则优于含2个参数的Coulomb强度准则、Hoek-Brown强度准则；Hoek-Brown强度准则优于Coulomb强度准则；广义Hoek-Brown强度准则、指数强度准之间的优劣难以比较。

3.2 实验数据的数量对拟合结果的影响

不同强度准则对同一组岩石实验数据删除2组高围压数据后参数的拟合结果见表3。

以Dunham白云岩为例，4种强度准则在删去2个高围压数据前后拟合曲线的变化程度见图2。

图14 种强度准则的平均拟合偏差柱状图

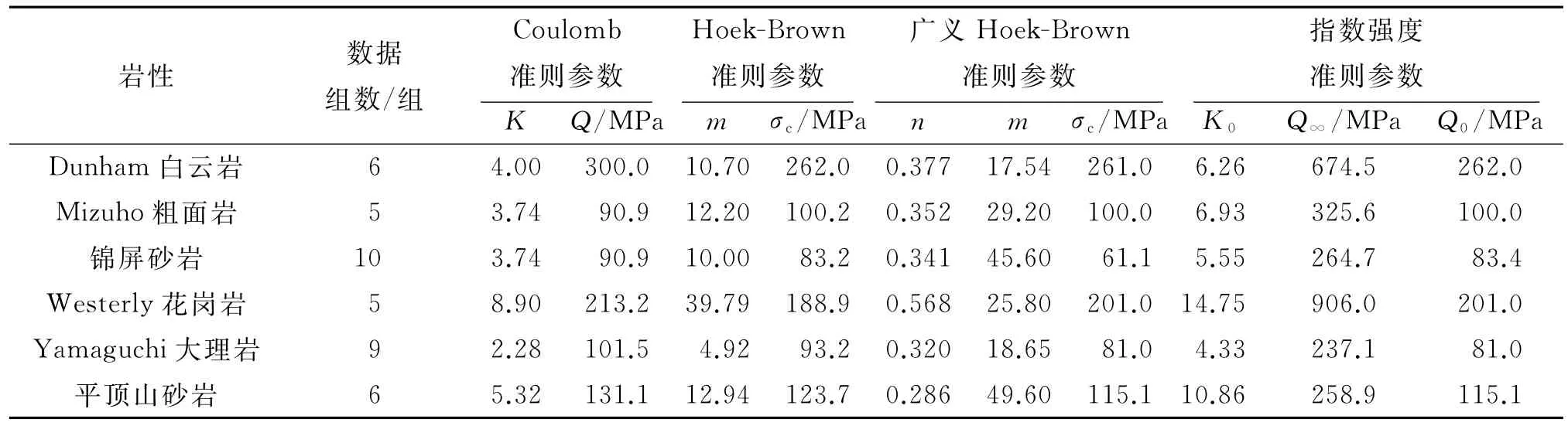
表34 种强度准则对6种岩石去掉2个高围压实验数据后的拟合结果

由图2可知：删除2组高围压后，Coulomb强度准则的拟合曲线与未删除之前的拟合曲线差异明显，Hoek-Brown强度准则的拟合曲线与未删除之前的拟合曲线差距较明显，广义Hoek-Brown强度准则和指数强度准则的拟合曲线与未删除之前的拟合曲线相比略有变化。说明含有3个参数的广义Hoek-Brown强度准则和指数强度准则更具有适用性，更能反映岩石的真实强度；含有2个参数的强度准则中，Hoek-Brown强度准则的适用性优于Coulomb强度准则；广义Hoek-Brown强度准则、指数强度准则之间的优劣则难以比较。

4 结论

（1）从4种强度准则对6种岩石的平均拟合偏差分析，含有3个参数的广义Hoek-Brown强度准则和指数强度准则的拟合特征优于含有2个参数的Coulomb准则和Hoek-Brown准则；Hoek-Brown准则优于Coulomb准则；广义Hoek-Brown强度准则和指数强度准则之间的优劣性难以比较。

（2）由4种强度准则对6种岩石实验数据删除2组高围压后的拟合曲线对未删除数据拟合曲线的预测性分析，含有3个参数的广义Hoek-Brown强度准则、指数强度准则更具有适用性，更能反映岩石的真实强度；如果剔除实验数据中的异常点，指数强度准则具有较小的拟合偏差。

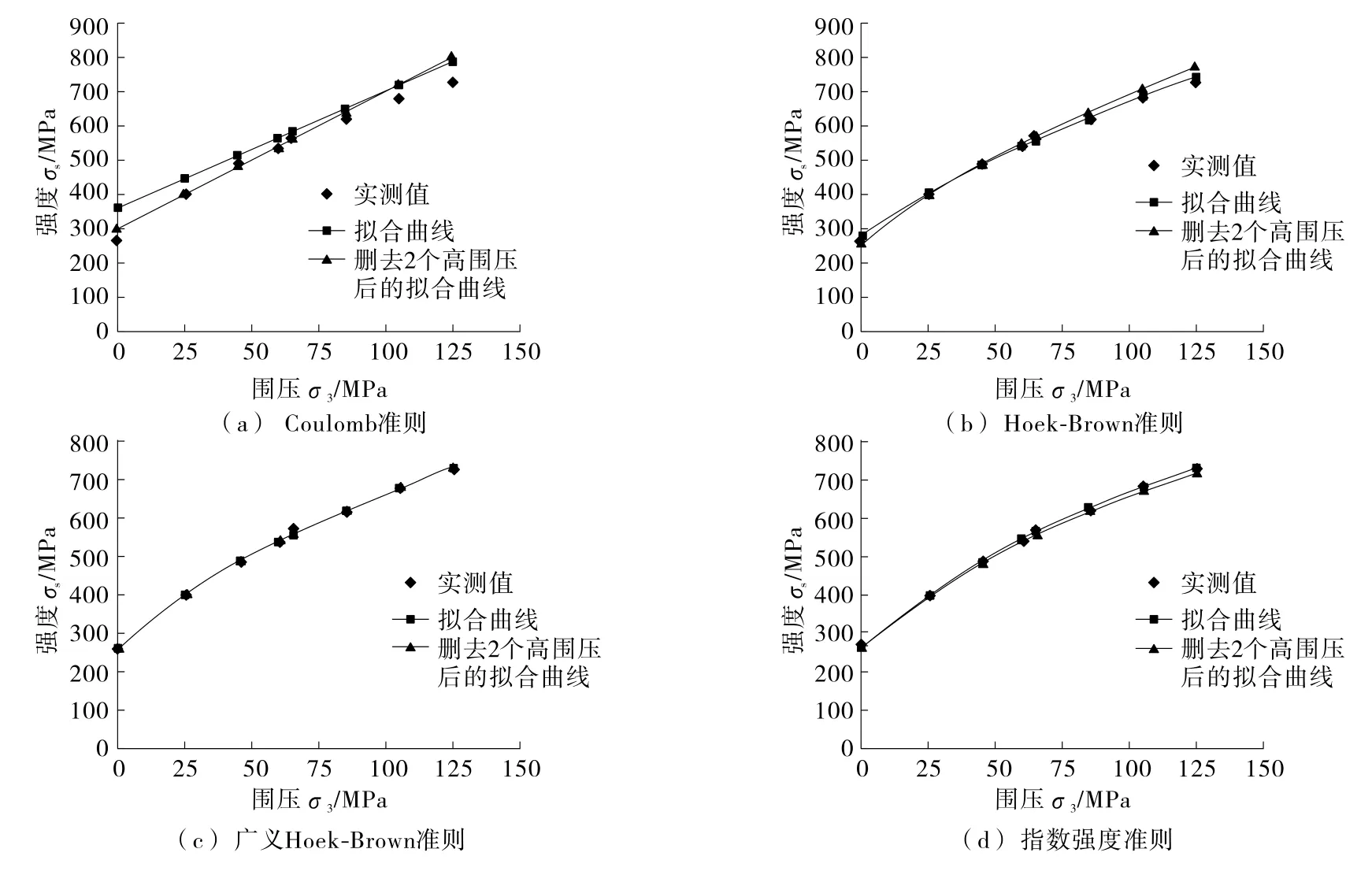
图2 Dunham白云岩在删去2个高围压数据前后4种强度准则拟合曲线对比

（3）由4种强度准则对6种岩石删除2组高围压后的拟合曲线对未删除实验数据的预测偏差分析，含有3个参数的广义Hoek-Brown强度准则、指数强度准则优于含有2个参数的Coulomb强度准则、Hoek-Brown强度准则；广义Hoek-Brown强度准则的预测偏差整体上比指数强度准则小；对于多数岩石，从预测偏差角度分析，广义Hoek-Brown强度优于指数强度准则。

［1］ 尤明庆.岩石强度准则的数学形式和参数确定的研究［J］.岩石力学与工程学报，2010，29（11）.

［2］ 尤明庆，苏承东.砂岩孔道试样压拉应力下强度和破坏的研究［J］.岩石力学与工程学报，2010，29（6）.

［3］ Haimson B，Chang C.A new true triaxial cell for testing mechanical properties of rock strength and deformability of Westerly granite［J］.International Journal of RockMechanics andMining Sciences，2000，37（2）.

［4］ Mogi K.Effect of the triaxial stress system on the failure of dolomite and limestone［J］.Tectonophysics，1971，11（2）.

［5］ Mogi K.Fracture and flow of rocks under high triaxial compression［J］.Journal of Geophysics Research，1971，76（5）.

［6］ Mogi K.Experimental rockmechanics［M］.London：Taylor and Francis，2007.

［7］ You M.Mechanical characteristics of the exponential strength criterion under conventional triaxial stresses［J］.International Journal of Rock Mechanics and Mining Sciences，2010，47（2）.

［8］ Von Kármán T.Festigkeitsversuche unter all seitigem druck［J］.Zeitschrift Verein Deutsche Ingenieure，1911，55.

［9］ You M.True triaxial strength criteria for rock［J］.International Jonmal of Rock Mechanics and Mining Sciences，2009，46（1）.

［10］ 汪斌，朱杰兵，邬爱清，等.高应力下岩石非线性强度特性的试验验证［J］.岩石力学与工程学报，2010，29（3）.

［11］ Al-Ajmi A M，Zimmerman R W.Relation between the Mogi and the Coulomb failure criteria［J］.International Journal of Rock Mechanics andMining Sciences，2005，42（3）.

［12］ 欧阳卫锋，王利利，王烁.岩石强度准则待定参数拟合方法及评价研究［J］.公路与汽运，2015（3）.

［13］ 苏承东，付义胜.红砂岩三轴压缩变形与强度特征的试验研究［J］.岩石力学与工程学报，2014，33（增刊）.

［14］ 昝月稳，俞茂宏.岩石广义非线性统一强度理论［J］.西南交通大学学报，2013，48（4）.

［15］ 吴黎辉.岩体经验强度准则研究［D］.西安：长安大学，2004.

［16］ 石祥超，孟英峰，李皋.几种岩石强度准则的对比分析［J］.岩土力学，2011，32（增刊）.

U416.1

A

1671-2668（2016）06-0083-04

2016-06-26