基于熵权模糊物元的电动汽车充电站选址研究

吴丽霞，王贝贝，胡静，李娜

（重庆交通大学交通运输学院，重庆 400074）

基于熵权模糊物元的电动汽车充电站选址研究

吴丽霞，王贝贝，胡静，李娜

（重庆交通大学交通运输学院，重庆 400074）

电动汽车充电站选址是一项复杂而繁琐的工作，文中从经济因素、环境因素、规划因素、交通因素4个要素层11个评价指标出发，在模糊物元模型的基础上，引入熵值法确定各指标权重，运用欧氏贴近度反映各方案指标值与指标值域的接近程度，建立评价充电站选址优良情况的熵权模糊物元模型，综合分析评价各备选方案，量化评价结果，得到最优方案。应用实例表明熵权模糊物元法能客观定量评价充电站选址问题，提高评价结果的精度。

公路交通；电动汽车充电站；选址评价；熵权；模糊物元；欧式贴近度

针对电动汽车充电站选址问题，文献［1］采用Delphi法建立了电动汽车充电站评价指标体系，利用灰色层次分析法确定各指标权重；文献［2］建立了基于可拓方法的电动汽车充电站选址评价模型，运用熵权法确定各评价指标的权重；文献［3］使用模糊评价方法对电动汽车充电站的选址进行了评价。上述研究建立的充电站选址评价指标体系不够完善，算法的实际操作性不强，且不能定量反映评价结果。该文基于电动汽车发展的实际情况，采用熵权模糊物元法建立电动汽车充电站选址评价模型，从备选方案中选出最优方案。

1 熵权模糊物元原理分析

1.1 模糊物元与复合模糊物元理论

物元是指用有序的三元组R=（M，C，x）来描述事物的基本元，其中M为指定名称的事物，x为特征C存在的量值，当量值x存在模糊性时，称为模糊物元。电动汽车充电站选址评价样本M中存在m个待评价指标C1，C2，…，Cm，与其相对应的模糊量值分别为x1，x2，…，xm，称R为m维模糊物元。Rnm表示n个待评价事物的m维复合模糊物元，则对应的模糊量值xji称为第j个样本的第i项指标的模糊量值（j=1，2，…，n；i=1，2，…，m）。Rnm表达式如下：

1.2 从优隶属度计算

从优隶属度表示每个单项评价指标Cm对应的模糊量值隶属于相应标准样本评价指标的模糊量值的程度。越小越优型评价指标的从优隶属度为：

越大越优型评价指标的从优隶属度为：

式中：xji为第j个样本第i项评价指标对应的量值，min xji为其最小值，max xji为其最大值。

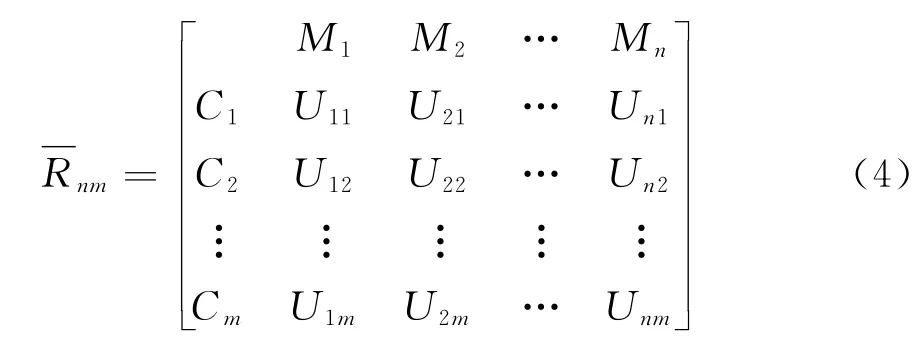
1.3 标准模糊物元和差平方模糊物元

通过式（4）构造样本m维标准模糊物元R0m，由复合模糊物元Rnm各待评价指标从优隶属度中的最大、最小值确定R0m中各项值，即：

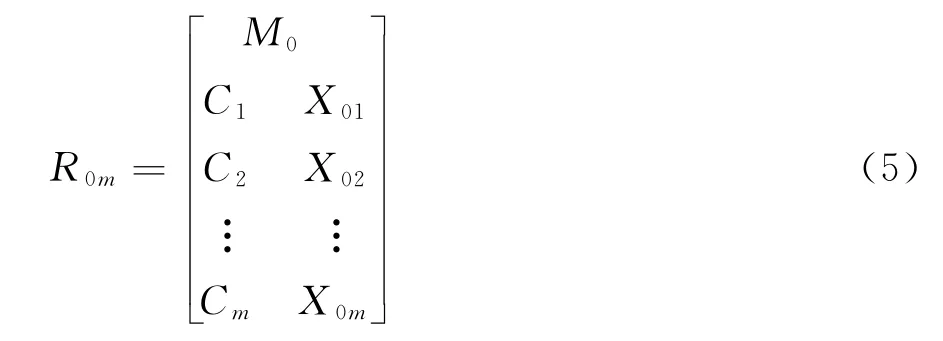
以Δij（j=1，2，…，n；i=1，2，…，m）表示标准模糊物元R0m与复合模糊物元Rnm各项的差的平方，得到差平方复合模糊物元RΔ：

式中：Δji=（u0i-uji）2；j=1，2，…，n；i=1，2，…，m。

1.4 熵权的确定

利用熵值法确定权重系数以避免人为主观因素造成评价结果偏差。在信息论中，熵值反映信息无序变化的程度，其值越大则系统无序程度越大，其值越小则系统无序程度越小，可用信息熵评价所获系统信息的有序度及效用，即由评价指标值构成的判断矩阵确定指标权重，使评价结果更符合实际要求。计算步骤：

（1）建立n个事物m 个评价指标的判断矩阵：

R=（xji）n×m（j=1，2，…，n；i=1，2，…，m）

（2）将判断矩阵进行归一化，得到矩阵B。对于越小越优型指标，B的元素按式（7）计算；对于越大越优型指标，B的元素按式（8）计算。

式中：在相同评价指标不同事物中，min xji代表最不满意者，max xji代表最满意者。

（3）定义熵。在n个评价事物m个评价指标的评价过程中，第i个评价指标的熵值Hi按式（9）计算。

（4）计算熵权Wi。计算公式为：

1.5 欧式贴近度与充电站选址评价

将欧式贴近度引入电动汽车充电站选址评价，反映待评指标值与标准指标值相互接近的程度，其值越大则两者越接近，其值越小则两者相距越远，可根据贴近度的大小对不同方案进行排序，得出最优方案。运用（*，+）算法建立计算欧式贴近度的复合模糊物元RPH：

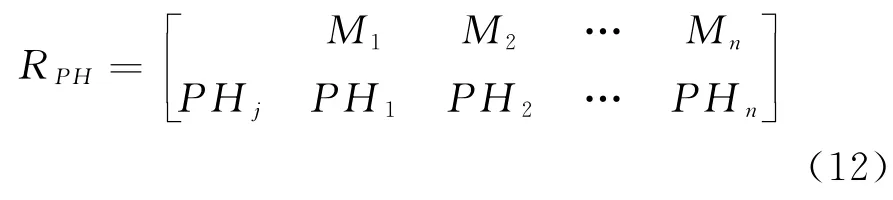
2 算例分析

2.1 评价指标的构建

电动汽车充电站的选址是一个复杂的决策问题，建立评价指标体系时应遵循相关性、独立性、可度量性和可实现性等原则。参考相关文献，建立包含4个要素、11个评价指标的电动汽车充电站选址评价指标体系（见表1）。

假设要在200万左右人口的大城市建立一个电动汽车充电站，为5 000～10 000辆各类电动汽车服务，相关参数取自文献［9］。电动汽车充电站候选地址有A、B、C 3个，其基本情况见表1。

2.2 建立评价模型

（1）构建复合模糊物元。根据表1构建A、B、C选址方案11个指标C1～C11的复合模糊物元。

（2）计算从优隶属度。根据评价指标的类型（越小越优型、越大越优型），分别按式（2）、式（3）对复合模糊物元进行处理，得到从优隶属度物元Rnm：

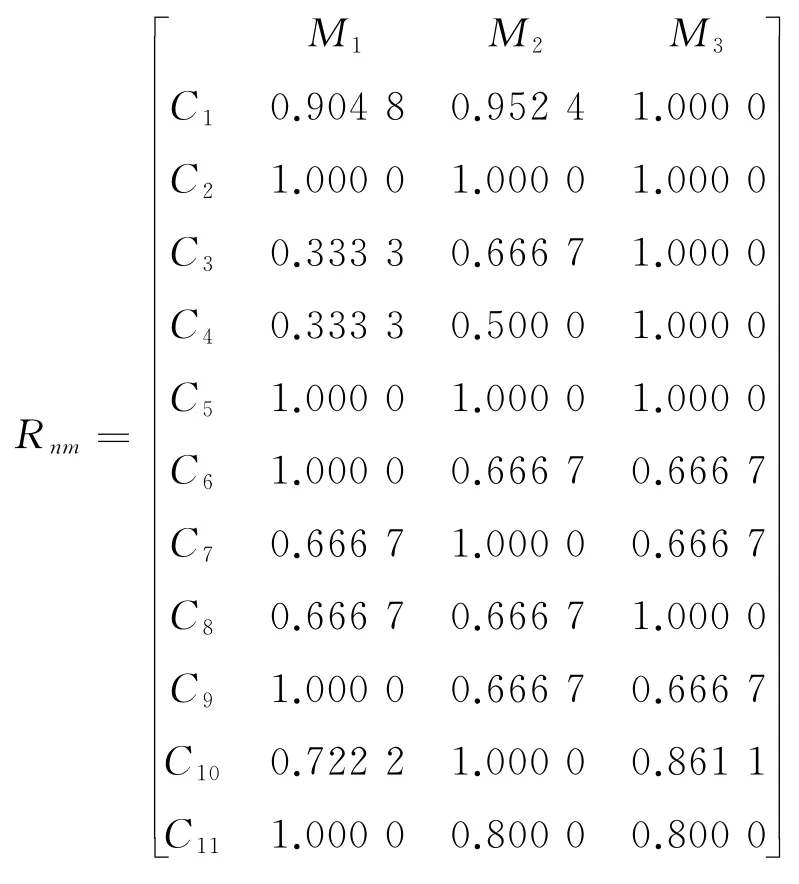
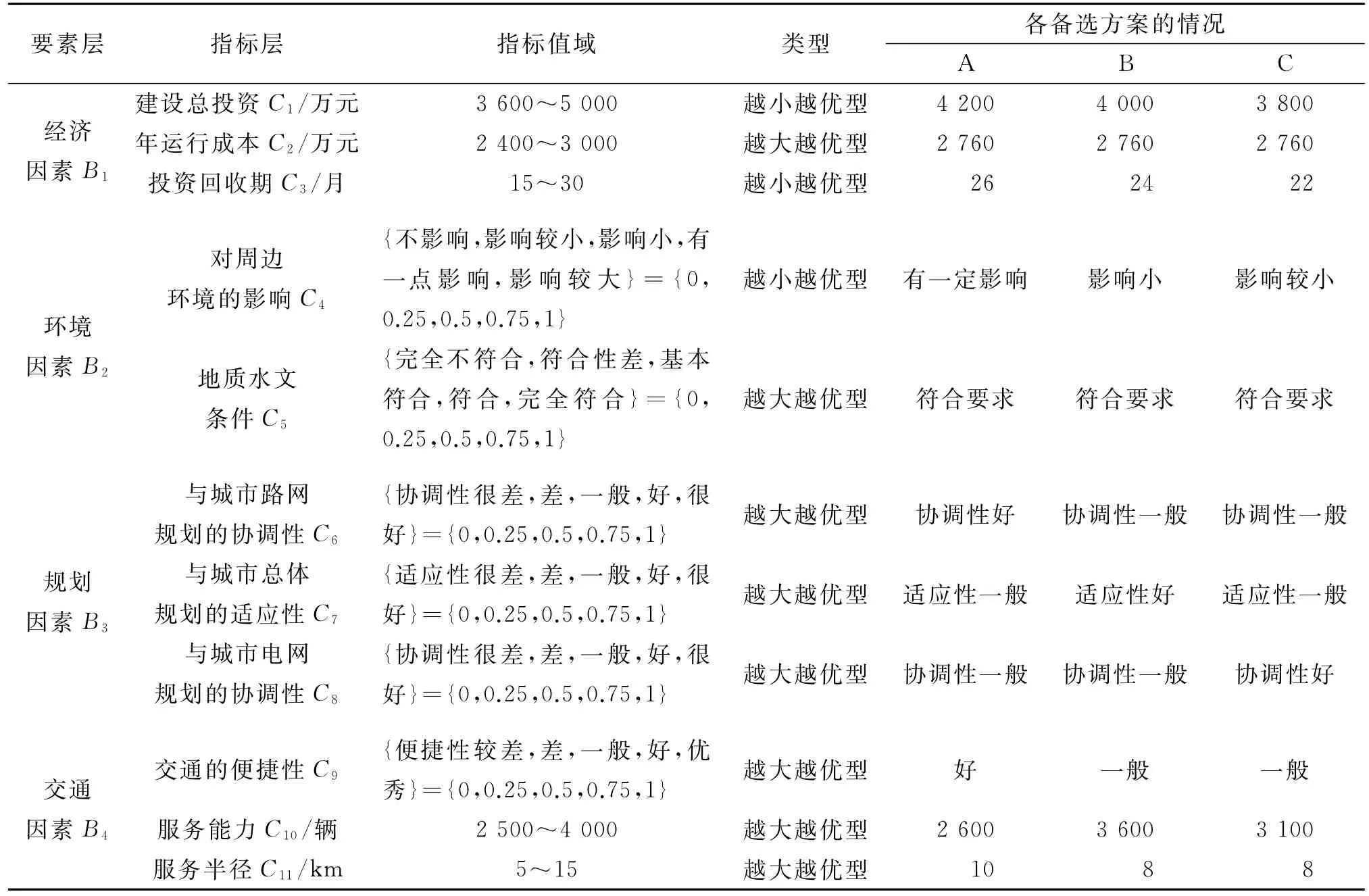
表1 电动汽车充电站评价指标体系及各备选方案的基本情况

（3）计算标准模糊物元和差平方模糊物元。由从优隶属度物元Rmn可知各评价指标最优隶属度均为1，按式（5）、式（6）进行处理，得到平方差复合物元RΔ：

（4）确定评价指标的权重系数。根据式（7）、式（8）构建指标层的归一化判断矩阵B，按式（9）～（11）计算评价指标的熵Hi、熵权Wi，得：

（5）欧式贴近度计算。由式（12）计算得到样本贴近度复合物元模糊矩阵RPH：

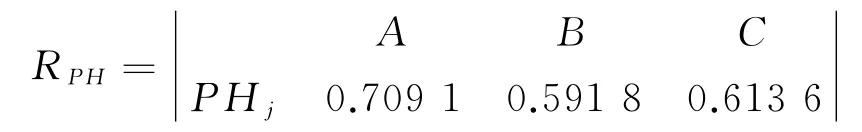
2.3 结果分析

根据欧式贴近度计算结果，3种方案的排列顺序为A＞C＞B，即A方案最好，C方案次之，B方案最差，方案A为该算例中充电站选址的最优方案。

3 结语

电动汽车充电站的选址具有不确定性、模糊性，且评价指标间可能不相关，选取充电站选址评价指标时需根据实际情况对指标进行筛选、定量。该文将模糊理论运用到充电站的选址方案评价中，建立了电动汽车充电站选址方案评价的熵权模糊物元理论模型，利用熵值法确定充电站选址评价指标的重要性，克服了凭经验确定指标权重的随意性，使权重计算更客观、合理。相比其他评价模型，熵权模糊物元模型在一定程度上量化了待评指标与评价等级的关联程度，以数字的形式直观反映各指标的关系，为充电站选址评价方案提供了量化的数字参考，是科学评价充电站选址方案的一种新方法。

［1］ 冯超，周步祥，林楠，等.Delphi和GAHP集成的综合评价方法在电动汽车充电站选址最优决策中的应用［J］.电力自动化设备，2012，32（9）.

［2］ 蔡子龙，束洪春，谢静，等.电动汽车充换电站选址规划的可拓评价研究［J］.数学的实践与认识，2013，43（21）.

［3］ 邱进煊，高春雷，王林信.电动汽车充电设施选址的模糊评价方案［J］.电力与电工，2012，32（2）.

［4］ 田静宜，王新军.基于熵权模糊物元模型的干旱区水资源承载力研究：以甘肃名勤县为例［J］.复旦大学学报：自然科学版，2013，52（1）.

［5］ 杨丽美，张维江.基于模糊物元模型的宁夏节水型社会效应评价［J］.人民黄河，2013，35（5）.

［6］ 施开放，刁承泰，左太安，等.基于熵权物元模型的耕地占补平衡生态安全评价［J］.中国生态农业学报，2013，21（2）.

［7］ 陈志凡，李勤奋，赵烨.基于熵权的模糊物元模型在农用地土壤健康评价中的应用［J］.中国土地科学，2008，22（11）.

［8］ 王萌，刘凯，牛利勇.电动汽车充电站选址决策与评价研究［J］.技术与方法，2015，9（2）.

［9］ 段万普.电动汽车技术与商业运行［M］.北京：中国电力出版社，2013.

［10］ 何霖，广晓平，李杨.基于熵权模糊物元分析的客运专线引入铁路枢纽的客运站选址方案研究［J］.兰州交通大学学报，2010，29（4）.

U492.1

A

1671-2668（2016）06-0045-03

2016-05-06