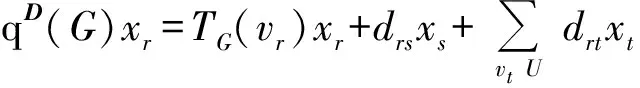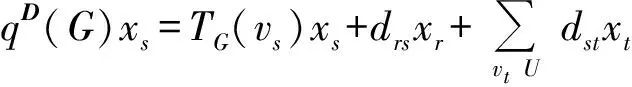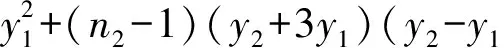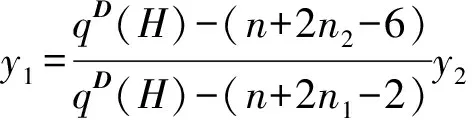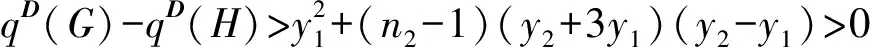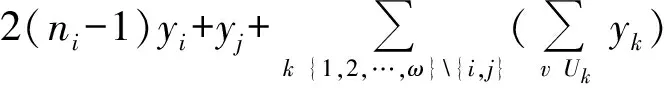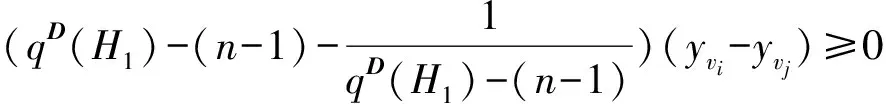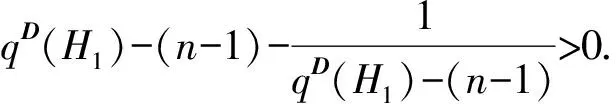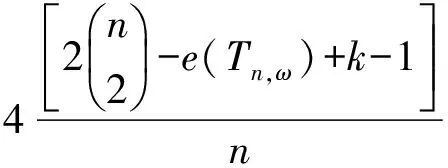给定团数的图的距离无符号拉普拉斯谱半径
2016-12-12李金溪尤利华
李金溪, 杨 墁, 尤利华
(华南师范大学数学科学学院, 广州 510631)
给定团数的图的距离无符号拉普拉斯谱半径
李金溪, 杨 墁, 尤利华*
(华南师范大学数学科学学院, 广州 510631)
设G是n阶简单连通图,T(G)表示图G的点传递度对角矩阵,D(G)表示距离矩阵,G的距离无符号拉普拉斯矩阵定义为:Q(G)=T(G)+D(G),相应的谱半径(即最大特征值)记作qD(G). 图G中一个相互邻接的顶点子集称为G的一个团,定义G的团数为其最大团的顶点个数,记作ω(G). 图G的一个正常着色是指使得G中任意2个相邻的顶点着不同颜色的一种着色方案. 在G的所有正常着色中,所需颜色数目的最小值称为G的色数,记作(G). 显见,(G)≥ω(G). 为了研究给定团数ω(G)=ω的n阶简单连通图G中取得最小距离无符号拉普拉斯谱半径的极图,文中综合运用代数、矩阵论与图论等方法,分如下2种情形进行讨论:(1)(G)=ω(G)=ω;(2)(G)>ω(G)=ω. 证明了Turn图Tn,ω是团数为ω的n阶简单连通图中具有最小距离无符号拉普拉斯谱半径的唯一图.
连通图; 团数; 距离无符号拉普拉斯谱半径
Keywords:connectedgraph;cliquenumber;distancesignlessLaplacianspectralradius

另一方面,关于给定团数的图或有向图的谱半径、拉普拉斯或无符号拉普拉斯谱半径的研究,请参看文献[7-13].
所使用的方法技巧得益于文献[7]的启发,刻画了给定团数的连通图中取得最小距离无符号拉普拉斯谱半径的极图.
设M是n×n矩阵,1,2,…,n为M的特征值. 一般来说,M不是对称矩阵,所以其特征值可能是复数. 不妨假设|1|≥|2|≥…≥|n|. 把M的特征值的模的最大值|1|定义为M的谱半径,记为ρ(M). 由Perron-Frobenius定理可知:若M是非负矩阵,则其谱半径ρ(M)是M的一个特征值; 若M是非负不可约矩阵,则其谱半径ρ(M)=1是单根.
设G=(V(G),E(G))是连通图,其顶点集为V(G)={v1,v2,…,vn},边集为E(G). 对于任意的u,vV(G),以G中连接u、v的最短路的长度表示u、v两者之间的距离,记作dG(u,v)或duv. 对于任意的uV(G),以顶点u到G中其他所有顶点的距离的和表示顶点u的传递度(transmission),记作TG(u). 如果G中所有点的传递度相等,即TG(v1)=TG(v2)=…=TG(vn),称图G是距离正则图.
G的距离矩阵是n×n矩阵,记作D(G)=(dij),其中dij=dvivj. 显见,连通图G的距离矩阵是非负不可约矩阵,其距离谱半径定义为其距离矩阵D(G)的谱半径,即为D(G)的最大特征值,记作ρD(G). 事实上,顶点vi的传递度TG(vi)是D(G)的第i行的行和,其中1≤i≤n. 称对角矩阵T(G)=diag(TG(v1),TG(v2),…,TG(vn))为G的点传递度对角矩阵. AOUCHICHE和HANSEN[5]定义G的距离无符号拉普拉斯矩阵为:Q(G)=T(G)+D(G). 显见Q(G)是非负不可约的、对称的、半正定的. 定义连通图G的距离无符号拉普拉斯谱半径是其距离无符号拉普拉斯矩阵Q(G)的谱半径,即为Q(G)的最大特征值,记作qD(G).
V(G)中相互邻接的顶点子集是图G的一个团,定义G中最大团的顶点个数为G的团数,记作ω(G). 定义图G的一个正常着色是指使得G中任意2个相邻的顶点着不同颜色的一种着色方案. 在G的所有正常着色中,所需颜色数目的最小值称为G的色数,记作(G). 由于G包含一个大小为ω(G)的团,所以至少需要ω(G)种颜色来给G正常着色,因此(G)≥ω(G).
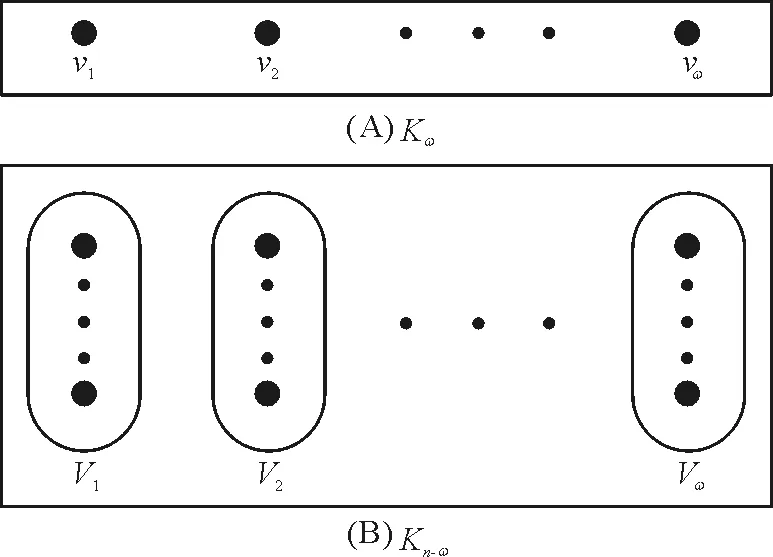
以Kn表示n阶完全图,顶点划分为V1,V2,…,Vr的完全r部图记作K|V1|,|V2|,…,|Vr|. 如果某个n阶完全r部图的顶点划分满足其每个部分的顶点个数尽可能相等,则称其为Turn图,记作Tn,r. 显然ω(Tn,r)=r.
其他的定义、术语以及未提到的符号可参看文献[14-20].
给出基本符号和定义后,紧接着寻求和证明在给定团数的连通图中取得最小距离无符号拉普拉斯谱半径的极图.
以下所考虑的图G为n阶简单连通图,其顶点集为V(G)={v1,v2,…,vn},边集为E(G),显见Q(G)=(qij)是不可约的、非负的、对称的和半正定的. 由Perron-Frobenius定理,qD(G)是单根并且有一个正的单位特征向量x=(x1,x2,…,xn)Tn与之对应,这里x被称作Q(G)的Perron向量. 从而,由
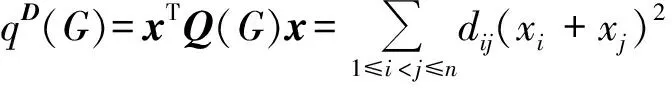
定义1[16]26设A=(aij)、B=(bij)是n×n阶矩阵. 如果对于所有的i和j都有aij≤bij,记作A≤B. 如果A≤B并且A≠B,记作A 引理1[16]27设A、B为n×n非负矩阵,其谱半径分别为ρ(A)、ρ(B). 如果A≤B,则ρ(A)≤ρ(B). 此外,如果A 根据引理1及Q(G)和qD(G)的定义,可得以下以图的语言来描述的推论. 推论1 设G是n阶图,H是G的生成子图,H和G均是连通的. 则 (i)qD(H)≥qD(G). (ii) 如果H是G的真子图,则qD(H)> qD(G). 推论2[2]1379设G为连通图,u、v是G中任意2个不邻接的顶点,G+uv表示G添加边uv,则qD(G+uv) 引理2 设G为连通图,x=(x1,x2,…,xn)T是Q(G)的Perron向量,NG(v)是G中与顶点v相邻的点集,vr,vsV(G). 若NG(vr){vs}=NG(vs){vr},则xr=xs. 证明 记U=V(G){vr,vs}. 由NG(vr){vs}=NG(vs){vr}及G的连通性,可知对任意的vtU有drt=dst,进而,由 可得TG(vr)=TG(vs). 注意到 故(qD(G)+drs-TG(vr))(xr-xs)=0.再由qD(G)>TG(vr),可得xr=xs. 引理3 设G是n阶连通图,其团数为ω(G)=ω. 若其色数(G)=ω(G)=ω,则qD(G)≥qD(Tn,ω),且等式成立当且仅当G≅Tn,ω. 证明 以Fn,ω表示所有色数等于ω的n阶图的集合. 不妨设GFn,ω是所有色数为ω的n阶图中具有最小距离无符号拉普拉斯谱半径的图. 下面将证明G≅Tn,ω. 由于添加边会减小距离无符号拉普拉斯谱半径,所以G必定是完全ω部图. 令V1,V2,…,Vω是V(G) 的一个划分使得G=K|V1|,|V2|,…,|Vω|. 不失一般性,对任意的k{1,2,…,ω},假设|Vk|=nk,且|V1|≤|V2|≤…≤|Vω|. 如果对任意1≤i 图1 从G到H的变化 设y为Q(H)的Perron向量. 由引理2可知Uk的所有顶点具有相同的Perron分量. 用yk表示Uk中顶点的Perron分量,其中k=1,2,…,ω. 显见,由于Perron向量y≫0,故对任意的k{1,2,…,ω}有yk>0. 注意到对任意viV1,有dG(u,vi)-dH(u,vi)=-1成立,对任意vjV2{u}=U2, 有dG(u,vj)-dH(u,vj)=1成立,且对任意的点对vs和vt,有dG(vs,vt)-dH(vs,vt)=0成立,故以下几个结论成立: (1)TG(u)-TH(u)=n2-n1-1;(2)对任意viV1,有TG(vi)-TH(vi)=-1;(3)对任意vjV2{u}=U2,有TG(vj)-TH(vj)=1;(4)对任意vtV(G)(V1∪V2),有TG(vt)-TH(vt)=0. 再由n1≤n2-2 qD(G)-qD(H)≥yT(Q(G)-Q(H))y= 下面证明y2≥y1. 注意到 qD(H)y1=(n+n1-1)y1+2n1y1+(n2-1)y2+ ∑k=3,4,…,ωnkyk, qD(H)y2=(n+n2-3)y2+(n1+1)y1+2(n2-2)y2+ ∑k=3,4,…,ωnkyk, 则 qD(H)y1-qD(H)y2=(n+2n1-2)y1-(n+2n2-6)y2, 设G是n阶连通图,其团数为ω(G)=ω. 下面分几种情形讨论:(i)ω|n; (ii)ω>n/2; (iii)ω 引理4(Turn’sTheorem)[7]387设G是不含ω+1团的n阶连通图,则G的边数e(G)≤e(Tn,ω),且等式成立当且仅当G≅Tn,ω. 引理5[3]3957设G是n阶连通图,则q(G)≥4σ(G)/n,且等式成立当且仅当G 是距离正则图. 引理6 设G是n阶连通图,其团数为ω(G)=ω,则 (i)qD(G)≥4σ(Tn,ω)/n,且等式成立当且仅当G≅Tn,ω. (ii)若ω|n,则qD(G)≥qD(Tn,ω)=2(n+n/ω-2),且等式成立当且仅当G≅Tn,ω. 图2 G(|V1|,|V2|,…,|Vω|)中一个ω团和一个(n-ω)团 Figure 2 Anω-clique and an (n-ω)-clique inG(|V1|,|V2|,…,|Vω|) 证明 不妨设H=G(|V1|,|V2|,…,|Vω|)是集合n,ω中具有最小距离无符号拉普拉斯谱半径的图. 若HG(0,0,…,0,1,1,…,1),那么必存在某个k{1,2,…,ω}使得|Vk|≥2. 不失一般性,我们假设i是最小的指数使得|Vi|=ni≥2,j是最大的指数使得Vj=∅(事实上,这样的j一定存在,因为令H1=G(|U1|,|U2|,…,|Uω|),其中V(Kω)={v1,v2,…,vω},U=U1∪U2∪…∪Uω=V(Kn-ω),且存在某个顶点uVi使得Ui=Vi{u},Uj={u},而对任意的k{1,2,…,ω}{i,j}均有Uk=Vk(图3). 显见,H1n,ω. 图3 从H到H1的变化 下面证明qD(H)>qD(H1). 令y是Q(H1)的Perron向量且分量yvk对应顶点vk(k=1,2,…,ω),由引理2,Uk的所有顶点有相同的Perron分量,并且用yk表示Uk中的顶点的Perron分量,其中k=1,2,…,ω. 很显然,由y≫0 可知对任意的k=1,2,…,ω,有yk>0 且yvk>0. 注意到dH(u,vi)-dH1(u,vi)=1,dH(u,vj)-dH1(u,vj)=-1,对任意的点对s和t,dH(s,t)-dH1(s,t)=0,且TH(vi)-TH1(vi)=1,TH(vj)-TH1(vj)=-1,对任意的点v,TH(v)-TH1(v)=0. 从而由瑞利商定理,可得 qD(H)-qD(H1)≥yT(Q(H)-Q(H1))y= (yvi+yvj+2yj)(yvi-yvj). 下面证明yvi≥yvj. 注意到 从而,qD(H1)(yvi-yvj)=(n+ni-3)yvi-(n-1)yvj+(ni-1)yi-yj. 又由ni≥2 可知n+ni-3≥n-1,ni-1≥1,因此 (qD(H1)-(n-1))(yvi-yvj)≥yi-yj. (1) 另一方面,注意到 (2) 由式(1)和式(2),可得 若qD(H)=qD(H1),则yvi=yvj,yi=yj且y也是Q(H)的Perron向量. 所以,0=qD(H)(yvi-yvj)=(n+ni-2)yvi-(n-2)yvj+niyi>0,矛盾. 因此,qD(H)>qD(H1),这也与H的定义矛盾. 证明完毕. 引理8 设G是团数ω(G)=ω的n阶连通图. 若ω>n/2,则qD(G)≥qD(Tn,ω),且等式成立当且仅当G≅Tn,ω. 证明 设U={v1,v2,…,vω}是G的一个团,且记W=V(G)U. 由于团数ω(G)=ω,从而对于V中的任意顶点来说,其最多有ω-1个邻点在U中. 这就意味着在图的同构的意义下,存在W的某个划分V1∪V2∪…∪Vω,使得G是G(|V1|,|V2|,…,|Vω|)的生成子图. 再由推论1和引理7,有qD(G)≥qD(G(|V1|,|V2|,…,|Vω|))≥qD(Tn,ω),且等式成立当且仅当G≅Tn,ω. 引理9 设ω、n为正整数且ω≤n,则 x1=q-(n+2k-4)q-(n+2k-2)x2. (6) 由式(4)和式(6),可得 q2-(3n+4k-6)q+(2n2+4k2-10n-12k+4nk+ 2k2ω+2kω+8)=0. (7) 解方程(7),易见式(3)成立. 令ω=n,由引理9可得 推论3[5]30qD(Kn)=2n-2. 引理10[21]设G是团数ω(G)≤ω的n阶连通图. 若(G)>ω且,则e(G)≤e(Tn,ω)-⎣. 由引理5和引理10,可得 显见e(Tn,ω)=(n2-n-2nk+k2ω+kω)/2,因此有 (8) 为了证明qD(G)>qD(Tn,ω),由式(3)和式(8),只需证明 (9) 化简式(9),接下来证明 nk(k+1)(n-ω-2kω)+[(k2ω+kω)-2(k-1)]2+ (k-1)(n2+2n+4nk)>0. (10) 令n=kω+k0,其中0≤k0<ω. 那么由式(10),有 4(k-1)2+kω[(k-1)(kω-2)+k0(k-3)]+ (k2+2k-1)k02+2k0(2k+1)(k-1)>0. (11) 为了证明式(11)是正确的,需证 (k-1)(kω-2)+k0(k-3)>0. (12) 注意到ω 定理1 设G是n阶连通图,其团数为ω(G)=ω,则qD(G)≥qD(Tn,ω),且等式成立当且仅当G≅Tn,ω. 子情形2.1:ω=n/2. 此时,由引理6可知结论成立. 子情形2.2:ω>n/2. 此时,由引理8可知结论成立. 子情形2.3:ω 结合以上情形的讨论,结论证明完毕. [1] GRAHAM R L,LOVSZ L. Distance matrix polynomials of trees[J]. Department of Mathematics,1978,29:60-88. [2] XING R D,ZHOU B,LI J P. On the distance signless Laplacian spectral radius of graphs[J]. Linear and Multilinear Algebra,2014,62:1377-1387. [3] XING R D,ZHOU B. On the distance and distance signless Laplacian spectral radii of bicyclic graphs[J]. Linear Algebra and Its Applications,2013,439:3955-3963. [4] TIAN F L,WONG D,ROU J L. Proof for four conjectures about the distance Laplacian and distance signless Laplacian eigenvalues of a graph[J]. Linear Algebra and Its Applications,2015,471:10-20. [5] AOUCHICHE M,HANSEN P. Two Laplacians for the distance matrix of a graph[J]. Linear Algebra and Its Applications,2013,439:21-33. [6] DAS K C. Proof of conjectures on the distance signless Laplacian eigenvalues of graphs[J]. Linear Algebra and Its Applications,2015,467:100-115. [7] ZHAI M Q,YU G L,SHU J L. Clique number and distance spectral radii of graphs[J]. Ars Combinatoria,2012,104:385-392. [9]LINHQ,SHUJL,WUYR,etal.Spectralradiusofstronglyconnecteddigraphs[J].DiscreteMathematics,2012,312:3663-3669. [10]GUOJM,LIJX,SHIUWC.ThesmallestLaplacianspectralradiusofgraphswithagivencliquenumber[J].LinearAlgebraandItsApplications,2012,437:1109-1122. [11]HEB,JINYL,ZHANGXD.SharpboundsforthesignlessLaplacianspectralradiusintermsofcliquenumber[J].LinearAlgebraandItsApplications,2013,438:3851-3861.[12]ZHANGJM,HUANGTZ,GUOJM.ThesmallestsignlessLaplacianspectralradiusofgraphswithagivencliquenumber[J].LinearAlgebraandItsApplications,2013,439:2562-2576. [13]HONGWX,YOULH.SpectralradiusandsignlessLaplacianspectralradiusofstronglyconnecteddigraphs[J].LinearAlgebraandItsApplications,2014,457:93-113. [14]BONDYJA,MURTYUSR.Graphtheorywithapplications[M].London:Macmillan,1976. [15]BONDYJA,MURTYUSR.Graphtheory[M].NewYork:Springer,2008. [16]BERMANA,ROBERTJP.Nonnegativematricesinthemathematicalsciences[M].NewYork:AcademicPress,1979. [17]HORNRA,JOHNSONCR.Matrixanalysis[M].England:CambridgeUniversity,1986. [18]MINCH.Nonnegativematrices[M].NewYork:JohnWileyandSonsInc,1988. [19]JENSENJB,GUTING.Digraphstheory[M].NewYork:Springer,2001. [20]BOLLOBSB.Extremalgraphtheory[M].NewYork:AcademicPress,1978. [21]KANGM,PIKHURKOO.MaximumKr+1-freegraphswhicharenotr-partite[J].MatematychniStudii,2005,24:13. 【中文责编:庄晓琼 英文责编:肖菁】 The Distance Signless Laplacian Spectral Radii of Graphs with Given Clique Number LIJinxi,YANGMan,YOULihua* (School of Mathematicsal Sciences South China Normal University, Guangzhou 510631, China) LetGbe a simple connected graph, T(G)bethediagonalmatrixofvertextransmissionofGandD(G)bethedistancematrixofG,thedistancesignlessLaplacianmatrixofGisthen×nmatrixdefinedasQ(G)=T(G)+D(G),andthedistancesignlessLaplacianspectralradiusofG,denotedbyqD(G).Recallthatacliqueofagraphisasetofmutuallyadjacentverticesandthecliquenumberω(G)isthenumberofverticesinthelargestcliqueinG.Thechromaticnumber(G) is the smallest number of colors needed to color the vertices ofGsuch that any two adjacent vertices have different colors. It is clear that(G)≥ω(G). In order to look for what’s the extremal graph with the minimal distance signless Laplacian spectral radius among all simple connected graphs with given clique numberω, this paper investigates the following two cases by combining the methods in the graph theory, algebra and matrix theory: (1)(G)=ω(G)=ω; (2)(G)>ω(G)=ω, and shows that Turn graphTn,ωis the unique graph having the minimal distance signless Laplacian spectral radius among all simple connected graphs withnvertices and given clique numberω. 2015-10-28 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(11571123); 广东省自然科学基金项目(2015A030313377) O151.21 A 1000-5463(2016)06-0118-06 *通讯作者:尤利华,教授,Email:ylhua@scnu.edu.cn.