浅谈高中立体几何入门之两招半

雍明亮

（广东省广州市从化区第二中学）

浅谈高中立体几何入门之两招半

雍明亮

（广东省广州市从化区第二中学）

在空间立体几何入门教学中，教师经常是投入多、收效少，学生上课似乎听得似是而非，课后遇到题目就一筹莫展的严重现象，这极大地影响了教师和学生学习的积极性。没有建立立体感和空间观念、基础知识不牢固，最终导致很多学生头脑中没有形成良好的立体几何认知结构，对立体几何入门教学给出了建议。

立体几何；图形；转化

高中必修2的立体几何部分，肩负着培养学生空间想象能力和逻辑思维重要内容。实际教学中，还是明显感觉到大多数学生对《立体几何》这部分内容存在畏惧心理，普遍感到困难！以至于部分学到了高三还是令许多学生望而生畏！难在何处？究其原因，无外乎如下两点：初、高中思维模式差；平面与空间的思维跨度。

其实，我们就是生活在三维空间中，学生的空间想象并不差，与其说是空间想象能力和逻辑思维能力较差，倒不如说是观察能力和发散思维能力的欠缺。在课堂上，为什么会有许多学生谈虎色变，摸不着头脑呢？其实，就是没有入门，没有掌握思维方法。针对“立体几何入门难”这一高中数学存在的普通问题，本文给出了解决方法。

第一招：图形——进入立体空间的敲门砖

空间立体几何与平面几何研究的基本对象相比多了两个“面”，而这多出的两个“面”，使研究的基本对象“立了起来”。在学习中，学生往往对空间概念模糊，在头脑意识中难以形成准确、直观的几何模型，以至于在解题时不会画图或画出图来也不易辨认，甚至作出错误的图形，阻碍了思维形成。学生感觉立体几何入门难的一个重要原因是认识对象从平面到空间的转变，不能很快适应。

因此，图形的学习和理解可以说是学习立体几何的难关。教师要从空间立体几何入门教学方面入手：

1.重视看图能力

在“空间几何体”的教学中，让学生自己动手做一些实物模型，如直线、平面、正方体、长方体、三棱锥等。通过对模型中的点、直、面之间位置关系的观察，逐步培养自己对空间图形的识别能力和想象能力，想象这些点、直、面在纸上的关系；同时，要掌握画直观图的规则，掌握实践、虚线的使用方法，为正确画图打好基础。另一方面，对于一个几何体，要从三视图——主视、侧视、俯视各角度去观察，体会不同的感觉，以开阔空间视野，培养空间感。

例如，正三棱锥的三视图中的主视、侧视是难点，如果只是教师在黑板或多媒体演示，学生很难理解为什么主视图三角形的腰长不是棱长，侧视图不是等腰三角形。通过学生自己动手做的正三棱锥模型，自己通过实物观察和教师的引导不难解决。

2.加强画图能力

在“空间几何体”的教学中，培养学生的画图能力，可从简单的图形（如直线和平面的各种位置关系）、简单的几何体（如正方体）画起。由参照模型画图，逐步过渡到没有模型也能准确地画出空间图形的直观图，且要画出具有较强的立体感，并能由直观图想象出空间图形。

例如，空间基本图形的直观图的表示与识别，虽然是简单，如果把握不好图形的要点，就会造成对识别复合图形错误的判断。画水平放置的正方形，部分学生画成如图的错误结果：

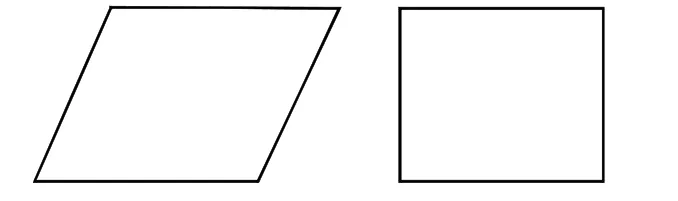
3.增强认图能力

所谓识图，就是指观察、分析和认识几何图形，既要由复杂的几何图形体看出基本图形，如点、线、面的位置关系，又要从点、线、面的位置关系联想到具体的几何图形模型。既要从所给图形中看到所画出的部分，又要想到未画出的部分。始终要记住在立体几何中识图的基本原则是“虚线看不见，实线看得见；平行能保持，垂直不保持”。

在教学过程中，教师以身作则，规范作图，在画立体图，或对照平面图，画出翻折图，以缩小对空间图形的陌生感和距离感，从而悟出空间图形与平面图形的差异与联系，从而正确、合理地作出图形。

看图、画图、认图是培养学生观察、动手、动脑的能力，只有观察透了，能准确作图，并能在头脑中形成清晰的空间图形，从“有模型”到“无模型”进而能正确分析、思考、想象各元素之间的关系，进而演绎和计算各种空间度量。对于入门的学生而言，提高观察能力、作图能力和想象能力是学好立体几何的有效途径。

在“空间几何体”的教学中，经过对实物、几何模型和空间图形的观察训练，学生已经具备了初步的空间想象能力，但在“空间点、直线、平面的位置关系”的教学中，观察的视角由几何体转向抽象的直线与平面等几何元素的位置关系，由于几何图形更加复杂和抽象，空间想象能力要求更高。因此，应注意培养学生使用几何模型的意识和应用方法。例如，利用长方体模型，探究定理，注重引导学生经历直观感知、操作确认、思辨论证的过程，从而提高学生几何的直观能力和几何的论证能力。

第二招：转化——打开空间思维的钥匙

1.加强三种语言的表述和转化训练

数学文字语言、符号语言、图形语言在立体几何部分结合是非常紧密的，它们在描述同一概念时形式各异，其本质属性是相同的，它们之间可相互转化，相辅相成。比如，立体几何的定理大都是用文字语言表述的，而证明它们时，则需先将文字语言翻译成图形语言，为数学思维提供几何直观，进而翻译成符号语言来推理、论证。立体几何问题是文字和图形，推理论证过程是符号语言。立体几何推理证明的过程实际上是几何的文字语言、图形语言和符号语言的转化过程。因此，三种语言的熟练转化是能否学好该部分内容的基础。

应当说立体几何部分是训练和培养学生三种数学语言互译能力的极好素材和时机。如果教师在进行立体概念、定理教学过程中，忽略了三种语言相互转化、翻译能力的训练，就容易造成不善于将这些文字语言与符号语言、图形语言相联系，只能死记硬背，从而也不可能达到真正理解，更妄谈应用能力的定理解题。

例如，我们可以用图形刻画几何元素的关系，辅助理解概念、定理和性质，可以避免死记硬背文字和符号的机械式学习。通过图形中的元素关系，让学生对照图形叙述相关定理或性质以及定理的使用条件。

例如，用图形表示垂直关系：

在解题中，若不能语言转化互译，合理画图，也就不能跨越解题的第一步。

如（课本习题）：三个平面两两相交，有三条交线，求证这三条交线交于一点或互相平行。

面对这道用文字语言表述的习题，学生往往感到难以下手，究其原因在于——画不出图形，不能理解题意；缺乏语言转化互译能力。若学生能用文字语言表述的题意翻译成图形语言，即：

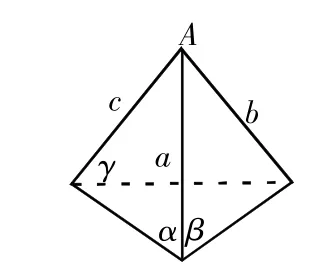
图1

图2

进而用符号语言表述为：

已知：α∩β=a，β∩γ=b，α∩γ=c，

求证：a、b、c相交于一点A或a、b、c相互平行，证明就不是难事了。

若学生缺乏语言互译能力，面对类似的题，就会无从下手。因此，在立体几何入门的概念、定理教学中，把握时机，提高学生的文字语言、符号语言、图形语言三种语言转化翻译的能力。在概念学习中反复训练，形成语言互译意识，那么在以后的解题过程中也就能自然而然地运用，从根本减少了学生解题过程中语言表述混乱的失误。

当然，三种语言相互转化翻译的能力，不只是在概念教学中需加强，而应渗透到立体几何教学的每个角落。它对学生的逻辑推理能力和语言组织能力将起着重要的作用。同时也将极大地改善“上课听得懂，课下题目不会做”“同学们怕做题”“老师们怕批改”的局面。

2.空间问题向平面问题转化

立体几何无论是内容还是方法，都是平面几何的延伸和拓展。把立体几何问题转化为平面几何问题，是研究立体几何问题最重要的数学思想方法之一。如，面面平行可以转化为线面平行，线面平行又可转化为线线平行；而线线平行常常由平面图形的中位线或平行四边形或平行公理得到。另外，线线、线面、面面平行与垂直的位置关系既互相依存，又在一定条件下不仅能纵向转化：线线平行（或垂直）、线面平行（或垂直）；面面平行（或垂直），而且还可以横向转化：线线、线面、面面的平行；线线、线面、面面的垂直。这些转化关系在平行或垂直的判定和性质定理中得到充分体现。平行或垂直关系的证明许多都是上述相互转化关系去证明。

所有上述这些都充分展现了转化的思想方法在立体几何中的“用武之地”。教学中应充分认识与恰当运用，通过强化思维的目标意识，增强思维的敏捷性和灵活性，提高学习效率。

半招：规范——严谨思维习惯的保证

数学都要有规范严谨，只不过此处尤为突出，这只能算是半招了。

教师作为教学引领者，必须为学生做好示范。这对刚接触立体几何的学生来说更为重要。从画图到论证过程的规范书写，都应为学生做好示范。在黑板上的示范切忌画图潦草，书写随意。对学生的作业从一开始就养成良好的习惯。

另外，培养学生的论证能力，是几何教学中的中心任务，是一个漫长的过程。在推理过程中，“言之有理，落笔有据”，“理、据”是指课本中给出的公理、定义、定理；不能想当然自造定理，也不能随意将习题的结论作为根据，更不能把平面几何结论在立体几何中不加证明地随意使用。在教学开始使用时，规范格式，抓住典型错误，反复强化，让学生养成习惯，培养学生的逻辑思维能力。

作为教学引领者的教师，要弄清培养学生各个阶段的要求，以由浅入深，从易到难，循序渐进。逻辑思维的形成、空间想象力的培养，任何学生都需要一个较长的过程，在教学中，我们要做好入门教学，实时关注引导学生，学生定会在立体几何学习中有很大的提高。

［1］杨冠夏.从立体几何入门教学看数学语言［J］.中学数学月刊，2007（2）.

［2］杜红全.立体几何入门教学之我见［J］.数学教育，2010（3）.

·编辑鲁翠红