基于ESO法的九宫板阻尼结构的优化设计方法

刘双燕， 李玉龙， 邓 琼， 徐一航

(西北工业大学 航空学院结构工程系先进结构和材料研究所，西安 710072)



基于ESO法的九宫板阻尼结构的优化设计方法

刘双燕， 李玉龙， 邓 琼， 徐一航

(西北工业大学 航空学院结构工程系先进结构和材料研究所，西安 710072)

利用渐进结构拓扑优化方法(Evolution Structural Optimization，ESO), 以约束阻尼层质量为约束条件，以最大模态损耗因子为目标函数,编制了ESO法的可执行程序，并基于ABAQUS软件建模，开展了九宫板约束阻尼层的拓扑优化研究。发现随着约束阻尼层的删除率增大，结构模态损耗因子逐渐增至最大值后降低。而随着删除率的增大，结构单位质量阻尼性能逐渐增大，可见优化布局可以提高九宫板结构的抑振性能。为研究优化布局对结构应力分布的影响，模拟了多种振动工况下，优化前后九宫板结构的Mises应力分布云图及其最大应力，结果发现优化布局后九宫板结构Mises应力分布影响很小，且最大Mises应力值得到有效降低。并将该方法应用在一般复杂结构的优化设计，实现了较少阻尼性能损失达到减重的目的，具有重要的工程实用性。

拓扑优化；灵敏度分析；约束阻尼结构

随着现代工业的飞速发展，机械结构的噪声和振动问题日益严重，特别是由此引起的振动疲劳问题[1]对桥梁建筑，机械结构，特别是飞行器结构产生重大影响。对结构进行阻尼处理是许多工业部门用来控制振动、噪声的一种有效方法。传统的阻尼材料减振设计中, 阻尼材料通常完全覆盖于待控结构表面, 设计过程就是确定使结构损耗因子取最大值时的阻尼材料类型、层数和厚度等,即阻尼材料配置优化设计。如BERTHELOT等[2]研究了纤维铺层角度对阻尼性能的影响。

对于很难完全铺设阻尼材料的结构，传统减振设计很难通过阻尼材料的分布，以最小的阻尼材料用量，达到最大的振动能量耗散，从而获得要求的结构动力学特性。然而，随着结构动力学拓扑优化有了长足的进步，对阻尼材料布局进行拓扑优化得以实现。

渐进结构拓扑优化方法(Evolution Structural Optimization，ESO)，通过逐步将无效或低效的材料删除,实现连续结构拓扑优化,避免了多变量数学规划求解。该方法是由XIE等[3]于1993年提出的,其优点是物理概念明确,可利用计算机的分析能力进行求解,避免了0～1整数规划的求解困难；设计变量少，每个单元只有1个存在与否的状态变量；可借助有限元分析软件,在计算机上实现迭代过程,算法的通用性好；灵敏度值由后处理近似得到,可节省结构重分析时间。郭中泽等[4-5]采用ESO方法,假设阻尼材料损耗因子为常数,以模态损耗因子最大化为目标函数,研究了约束阻尼板结构的拓扑优化布局问题。

茅志颖等[6]采用该ESO方法对结构微小损伤定位进行研究，结果表明，该方法可在结构整个区域寻找损伤点，即使微小的损伤结构也可以有很好的搜寻效果。

李超等[7]等以阻尼结构模态损耗因子最大化为目标，基于ANSYS软件编写基于ESO的软件程序，对圆柱壳体进行阻尼布局拓扑优化，取得了良好的结果。

柳承峰等[8]对约束层阻尼短圆柱壳进行拓扑优化分析并进行了实验研究。研究表明该拓扑优化方法正确，用于短圆柱壳约束层阻尼材料布局优化具有较强的工程实用性。

郑玲等[9]对振动声辐射环境下的约束阻尼板结构进行优化，研究表明:以声功率最小化为目标，对约束阻尼材料布局进行拓扑优化，能有效抑制结构的振动声辐射，为结构低噪声设计提供了重要的理论参考和技术手段。

九宫板结构是飞机上典型结构，其结构振动对飞机有很大影响，需要尽可能地降低其振动响应。

同时，近年来ABAQUS软件在振动分析方面广泛应用，但其相应的拓扑优化模块没有成熟应用。基于上述原因，本文针对工程上常用的九宫板结构，以特定阶或多阶模态损耗因子最大化为目标,采用ESO方法, 对约束阻尼结构模态损耗因子最大化的优化问题进行研究。利用C语言编制了ESO法的可执行接口程序，通过调用ABAQUS软件建模，实现四周固支九宫板约束阻尼层的拓扑优化研究，讨论了基于九宫板结构的拓扑优化布局在稳态响应条件下对结构Mises应力的影响。并进一步讨论在随机载荷下，拓扑优化布局对九宫板结构中心部位响应的影响。

1 优化问题的提出

对于一般的约束阻尼结构，其动力学基本方程为:

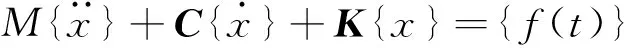
(1)

式中,M,C,K分别为结构质量、阻尼和刚度矩阵,{f(t)}为载荷矢量。对于给定的约束阻尼结构，其振动能量消耗主要来自于结构内部阻尼,因此建立拓扑优化模型时以九宫板结构的模态阻尼比作为目标函数,同时满足一定删除率的约束条件,以约束阻尼结构单元的拓扑变量xi为设计变量。拓扑优化模型为:

Maxη

findx=[x1,x2,……，xn]

其中,η为复合结构的模态阻尼比；xi为附加阻尼结构单元i的存在状态，0表示该单元被删除，1表示该单元为附加阻尼结构单元保留；Wv，Wc分别为阻尼结构和约束结构的质量；W*为附加阻尼结构的最大用量,Tv和Tc分别为阻尼结构和约束结构的厚度，T*为附加阻尼结构的最大允许厚度。

2 损耗因子及其灵敏度的推导

由模态应变能法[10]可知,结构的第k阶模态损耗因子的计算公式如下:

(2)

式中,ηv，ηc，ηb分别为阻尼材料、约束材料和基础结构的损耗因子；Evk，Eck，Ebk分别为阻尼材料、约束材料和基础结构第k阶模态应变能；Etk为复合结构第k阶总的模态应变能，即Etk=Evk+Eck+Ebk；

基于郭中泽等的研究[4],并考虑约束层材料的阻尼性能，复合约束阻尼结构k阶模态损耗因子对阻尼材料单元i存在状态的灵敏度为:

(3)

如果前M阶模态损耗因子最大化,则模态损耗因子灵敏度为:

(4)

当所有灵敏度全部为负数时,在优化过程中,逐步删除灵敏度绝对值最小的单元,使模态损耗因子沿最缓慢的路径下降;当灵敏度有正有负时,在优化过程中,删除具有最大灵敏度(正数)的单元,使得阻尼结构的结构损耗因子增加量最大。

由于在优化过程中存在棋盘格式和网格依赖性等不稳定现象，采用离散型网格滤波进行控制。滤波采用Sigmund滤波技术，滤波后单元i的模态阻尼比敏度变量为:

(5)

式中,xj为拓扑设计变量，Hi为单元i的权重因子。Hi的大小与该单元和当前计算单元的中心距成反比，且Hi≥0，其计算如下：

Hi=max(0,r-dist(i,j))

(6)

式中,r为滤波半径，dist(i,j)为单元i和当前计算单元的中心距离。

3 优化过程的实现

首先利用Python语言编制主程序调用ABAQUS软件，实现结构有限元建模分析和计算结果，然后利用C语言编制程序实现灵敏度分析和滤波分析以及实现循环进行。整个优化设计过程如图1所示。

具体的实现步骤为：

(1)利用ABAQUS软件建立基础结构和表面完全覆盖阻尼材料组装的有限元模型，并进行结构分析，并输出各个单元的模态应变能。

(2)利用C语言进行计算结果处理，求出相应模态的结构损耗因子。

(3)根据式(5)计算结构中各阻尼单元的模态损耗因子灵敏度,并进行独立网格滤波。

(4)比较滤波后的灵敏度因子，判断是否满足过滤条件，若满足过滤条件则删除相应单元，返回步骤(1)继续计算，反之执行步骤(5)。

(5)删除准则进化，判断是否满足该优化问题的约束条件，若不满足，则返回步骤(1)继续计算，反之结束优化程序。

图1 优化总体流程图Fig.1 Topological optimization overall flow chart

4 九宫板阻尼结构的优化布局

以控制约束阻尼材料质量为条件，寻找约束阻尼层在九宫板上的最优拓扑分布，使九宫板复合阻尼结构的第一阶模态损耗因子最大。

九宫板的有限元模型如图2所示，其平板尺寸为430 mm×480 mm×1.5 mm；初始阻尼层的尺寸为430 mm×480 mm×1mm；初始玻璃纤维板的尺寸为430 mm×480 mm×0.2mm；阻尼材料和玻璃纤维板的力学性能分别如表1～表3所示。

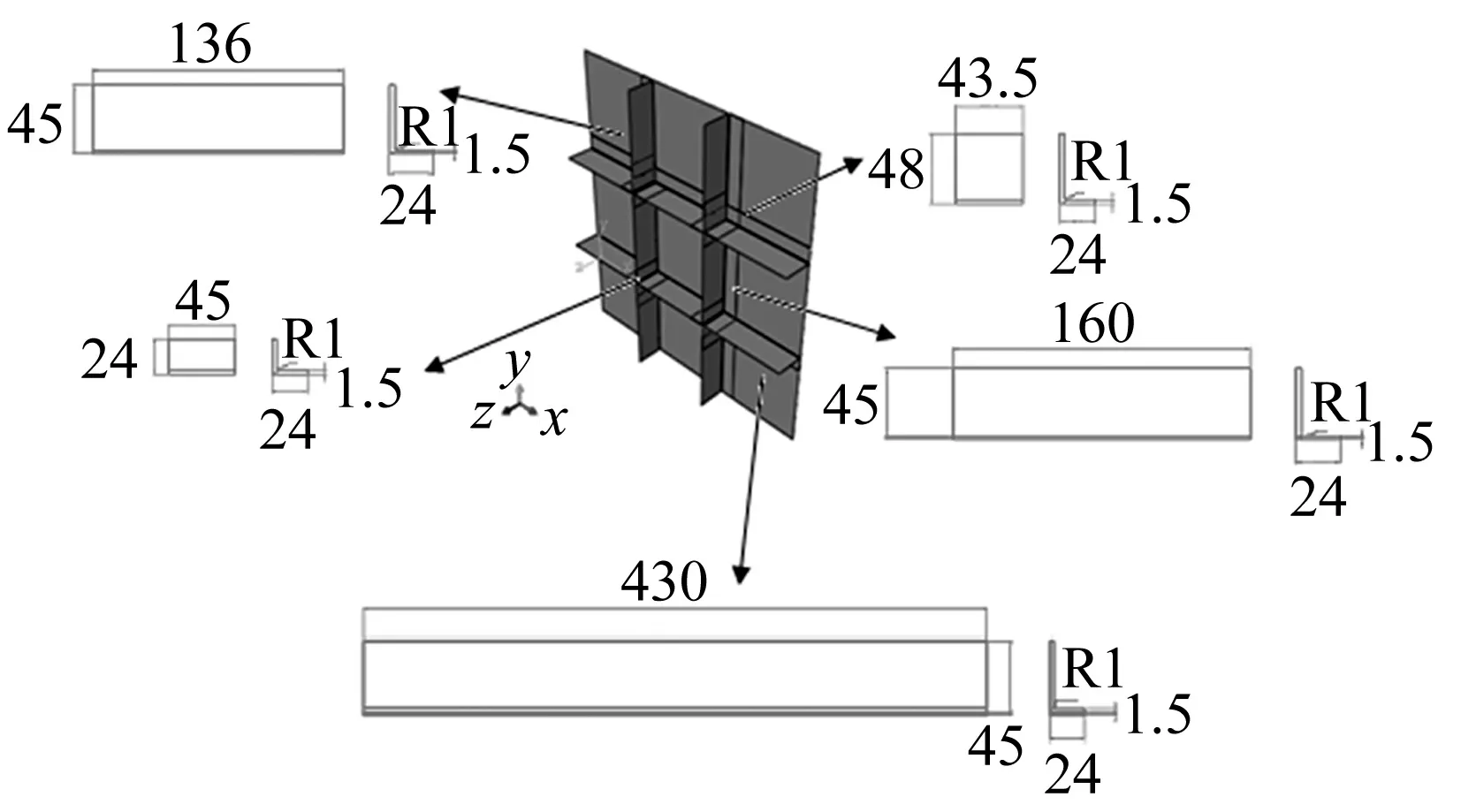
图2 九宫板的有限元模型Fig.2 Finite element model of 3×3 grid stiffened panel表1 2024铝合金的力学性能Tab.1 Mechanical property of 2024 alloy

材料密度/(kg·m-3)弹性模量/MPa泊松比AL2780700000.346

表2 3M112D力学性能Tab.2 Mechanical property of 3M112D

表3 单向玻璃纤维板力学性能Tab.3 Mechanical property of uni direction glass fiber plate

本文选取滤波半径r=10,删除单元数量小于50个，网格尺寸为5 mm, 约束层和阻尼层分别含有8 256个单元，其中阻尼层采用C3D8R，其他结构采用S4R网格类型，按照前文所述的优化步骤对九宫板结构进行优化，图3(a)～图3(i)给出了黏弹性阻尼材料删除率分别为10%、20%、30%、40%、50% 、60%、70%、80%和90%条件下的九宫板的约束阻尼梁结构最优拓扑分布。从图中可以看出随着删除率的增大，开始删除位于九宫板结构的四个角落的约束阻尼部分，当删除率为40%时，剩余的约束阻尼结构呈十字花瓣型，之后随着删除率继续增大，十字花瓣型约束阻尼从较短边的花

瓣开始删除，最后到删除率为90%时，约束阻尼层只余下位于九宫板结构中心位置的部分。由于复合阻尼九宫板结构的轴对称性使得其拓扑布局呈对称性。

表4给出了不同删除率下复合九宫板的一阶模态损耗因子，不考虑阻尼时结构的频率(f0)，考虑阻尼时的结构频率(f0*)，附加约束阻尼与九宫板质量之比(△m/m(al))以及复合九宫板结构的总质量的数值。

由表4可以看出，粘贴有约束阻尼层的九宫板结构的一阶固有频率在整个优化过程中，变化很小，其变化幅度小于5%，说明在整个优化过程中附加质量对结构刚度影响很小。

图3 九宫板复合阻尼结构的最优拓扑构型Fig.3 Topological layout of the 3×3 grid stiffened panel with removal ratio表4 拓扑优化对九宫板复合阻尼结构频率和阻尼影响Tab.4 The influence of topological layout on the frequency and loss factor of the variable section beam

删除率ηf0频率/Hzf*0频率/Hz△m/m(AL)复合九宫板质量/kg02.80%392.84392.6939%2.000.12.78%392.85392.7035%1.950.22.77%392.89392.7431%1.890.32.75%393.11392.9627%1.830.42.77%393.96393.8123%1.780.52.86%395.41395.2519%1.720.63.43%397.25397.0216%1.670.73.59%398.37398.1112%1.610.84.00%400.29399.978%1.550.93.87%401.63401.334%1.50

随着删除率的增大，九宫板结构的一阶频率略微增大，原因是粘贴的附加阻尼结构的柔性较九宫板基板材料的柔性大。

为了更直观的研究附加阻尼结构对复合阻尼九宫板结构的影响，图4给出了不同删除率下相应的复合阻尼九宫板结构的模态损耗因子。

由图4可知，当约束阻尼结构的删除率小于等于40%时，整个复合阻尼九宫板结构的模态损耗因子略略降低，降幅小于2%，结合拓扑优化的构型，说明四个角落处的约束阻尼部分对阻尼性能的敏感度较小；当删除率大于等于40%之后，相应的复合阻尼九宫板结构的模态损耗因子缓慢增大，至80%时，达到最大值，当删除率为90%，复合阻尼结构的模态损耗因子微降，说明铺设在九宫板中间部分的附加阻尼结构对九宫板结构的抑振性能提高有很大贡献。随着删除率的增大，模态损耗因子逐渐增大，是由于在删除过程中，结构中每个单元的灵敏度随之变化，对阻尼的贡献值不同。

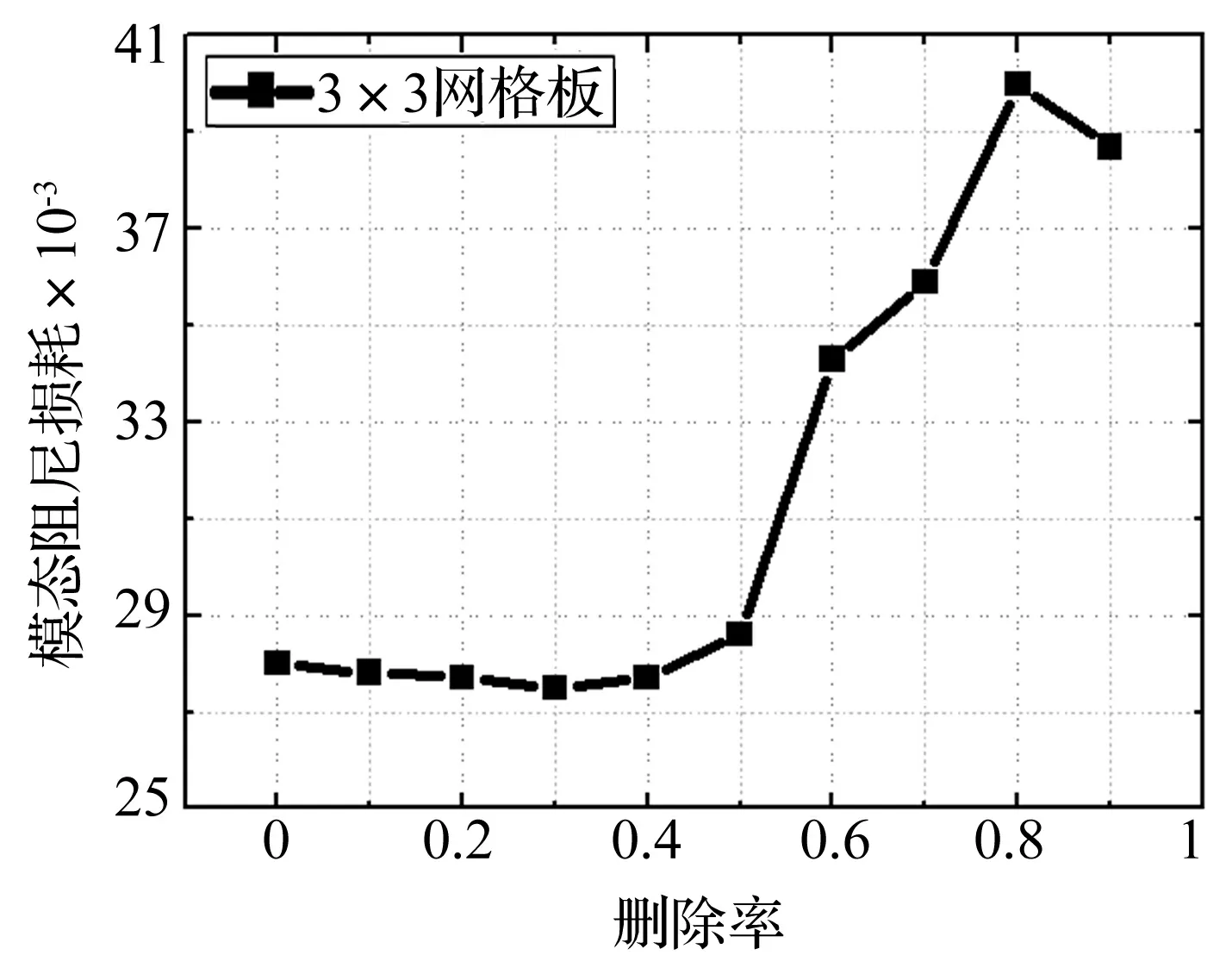
图4 不同删除率下阻尼结构的模态损耗因子Fig.4 The modal loss factor of the constrained damping structure attached on 3×3 grid stiffened panel by different removal ratio

而另一方面，随着约束阻尼结构删除率的增大，其相应的附加质量减小，为了排除附加约束阻尼结构质量对整个复合结构的阻尼性能影响，本文选用单位质量的阻尼损耗因子作为纵坐标，删除率作为横坐标，画出了归一化的模态损耗因子随删除率的变化规律图，如图5所示。

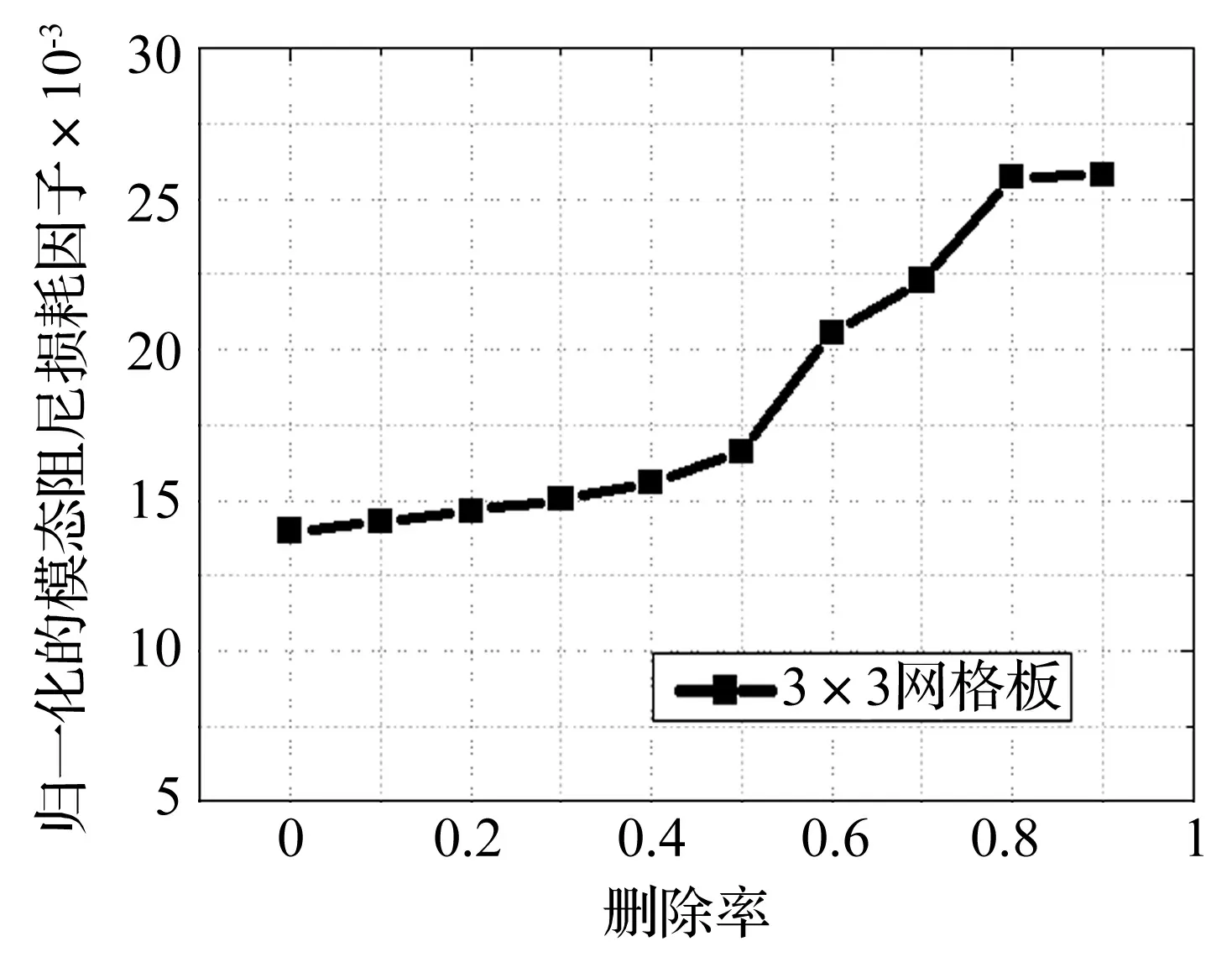
图5 单位质量模态损耗因子随删除率变化情况Fig.5 The normalization modal loss factor of the constrained damping structure attached on 3×3 grid stiffened panel by different removal ratio

图5表征了单位质量结构的模态损耗因子随删除率的变化情况，可以看出随着删除率增大，单位质量的模态损耗因子增大，说明随着删除率的变化，结构单元灵敏度在不断变化，表明采用拓扑优化技术，可充分利用阻尼材料的空间拓扑布局，使结构保持较高的振动能量耗散特性。

随着删除率的增大，约束阻尼层的质量逐渐减少，其附加质量与九宫板结构的质量比重从全铺层时的39%降至删除率为90%时的4%，质量比重变化较大，且铺层处单元约束阻尼层与铝板质量比为65%，拓扑优化过程中删除局部约束阻尼层，可能引起结构局部的应力集中，为了研究局部单元敷设对结构应力集中的影响，本文选取了全铺设约束阻尼层，删除率为50%的优化布局，以及无铺设的九宫板结构三种布局情况，在四边固支条件下，采用直接稳态动力学分析，研究了共振频率下优化前后结构的Mises应力分布，模态阻尼代入前文计算的结果，载荷为随正弦振动的单位面压，其频率值等于该结构的一阶固有频率。图6(a)～图6(c)分别给出了全铺设，优化铺设，无铺设时九宫板的Mises应力云图。

图6 不同删除率下， 在一阶固有频率时的Mises应力分布云图Fig.6 Mises stress distributed contour of the constrained damping structure attached on 3×3 grid stiffened panel on the first frequency by different removal ratio

图6可以看出，一阶固有频率处，不同删除率下九宫板的平板上的应力分布云图基本相同，只是应力值大小不同。为了研究不同删除率下，不同模态损耗因子下的应力分布差异因素，图7给出了九宫板结构最大Mises应力和相应的模态损耗因子下随删除率变化趋势图。

图7 九宫板结构的最大Mises和损耗因子随删除率变化图Fig.7 The maximum Mises stress value and the first modal loss factor of the constrained damping structure attached on 3×3 grid stiffened panel by different removal ratio

从图7可以看出Mises(rr=1)>Mises(rr=0)> Mises(rr=0.5),并且η(rr=1)<η(rr=0)<η(rr=0.5),结构的阻尼损耗因子与其最大Mises应力成负相关，当结构的阻尼损耗因子较大时相应的Mises应力值较低，当删除率为0，采用全铺层时，九宫板的最大Mises应力为8.91E+003 Pa,比没有铺设约束阻尼结构时的值(2.02E+004 Pa)降低了56%，说明采用约束阻尼铺层结构可以有效得提高结构的阻尼性能并且降低在共振条件下结构的最大Mises应力。

九宫板结构采用全铺层布局比优化布局的最大Mises应力要大，归根于其阻尼值较小，说明附加约束阻尼结构在九宫板结构上的优化布局对其阻尼性能和共振条件下的Mises应力分布具有重要影响，可以在轻量化约束阻尼层的基础上，提高其阻尼性能并降低其共振条件下的应力分布，对九宫板等复杂结构的抑振研究很有意义。

结构的模态损耗因子是结构振动性能的重要参数，其值越大，则结构的振动响应越小。而在实际工程应用中，结构易受的激励是随机激励，特别是对于飞机结构而言，九宫板结构中心隔板处振幅最大，有效的降低其中心位置的动态响应是结构抑制振动的关键。而对于飞机结构中典型的九宫板而言，其中心位置的响应主要由一阶模态贡献，因此实现中心点的抑振，可以简化为其一阶模态损耗因子最大化的问题。为了研究随机振动条件下，拓扑优化引起的阻尼性能提高对结构响应更为直观的影响，本文选取了在全铺设，删除率为50%及无铺设约束阻尼层时的九宫板布局为对象，比较了在基础随机激励为l g2/Hz,316.2～417.3 Hz频率范围内的白噪声，四边固支的九宫板结构中心点处的垂直于九宫板面板方向的加速度值(A3)。其结果如下表5所示。

表5 拓扑优化对九宫板复合阻尼 结构中心点加速度响应的影响Tab.5 The influence of topological layout on acceleration at the center of the 3×3 grid panel with constrained damping layers

在随机振动条件下，九宫板结构中心点的加速度响应随着阻尼值的增大而减小，减小而增大，当阻尼层从优化前的2.8%到优化后的2.86%，其中心点垂直面板的加速度值仅仅为优化前的30%，没有铺设约束阻尼层的九宫板结构的加速值是全铺设结构的17倍，是优化后的87倍，因此，尽可能提高结构的模态阻尼比是抑制振动的最有效方法。因此在九宫板拓扑优化中，可以用九宫板一阶模态最大化来近似结构中心点的加速度响应最小化。

5 复杂结构的优化布局

九宫板结构是飞机的基础结构件，事实上，飞机的机翼内部是多个九宫板结构拼接而成，不同的结构件其优化局部结果不同，阻尼性能也不同，本文将以九宫板为基本结构扩展成如图8(a)所示的包含4个九宫板结构的复杂结构。材料参数，优化流程，同上文简单九宫板。目标为删除率为50%时,模态阻尼最大化，网格尺寸为5 mm,由九宫板拓展的复杂结构含有59 072个单元，约束层和阻尼层分别含有33024个单元，其中阻尼层采用C3D8R，其他结构采用S4R网格类型，优化过程中的过滤半径为50，循环一次删除单元小于300个，最终优化布局如图8(b)所示。

图8 复杂结构有限元模型及优化布局Fig.8 The finite model and optimal layout with removal ratio 50% of the complex structure

在优化过程中的损耗因子随删除率的变化趋势如图9所示。

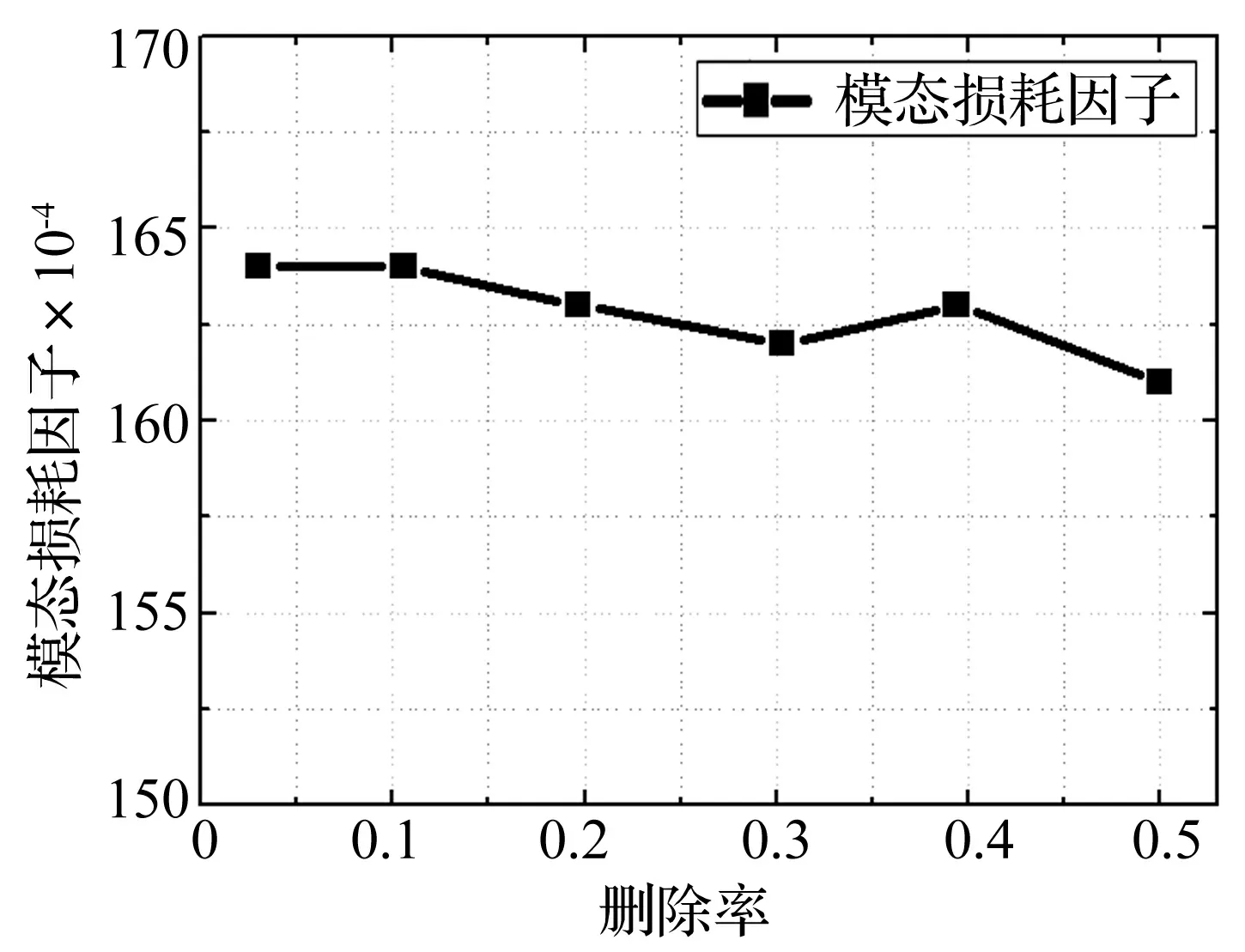
图9 不同删除率下复杂结构的模态损耗因子Fig.9 The modal loss factor of the constrained damping structure attached on 3×3 grid stiffened panel by different removal ratio

从图9可以看出，随着删除率的增大，敷设约束阻尼层的模态损耗因子缓慢减小，当删除率为50%时，其阻尼值下降仅仅约3%，达到了降重的目的且阻尼性能牺牲很小，可以说明基于ESO的拓扑优化方法可以实现在较少的附加质量的情况下实现复杂结构的抑振效果，该方法可以广泛应用于一般阻尼结构的抑振优化设计，有很强的工程实用性。

6 结 论

本文编制了可执行软件，基于ABAQUS软件，实现九宫板阻尼结构的拓扑优化。相应的研究结果如下：

(1)当约束阻尼结构的删除率小于等于40%时，整个复合阻尼九宫板结构的模态损耗因子基本没有变化；当删除率大于40%时，相应的复合阻尼九宫板结构的模态损耗因子逐渐增大，至80%时，达到最大值，当删除率为90%时，复合阻尼结构的模态损耗因子微降，特别地，随着删除率的增大，结构的单位质量阻尼性能随之增大，说明铺设在九宫板中间部分的附加阻尼结构对九宫板结构的抑振性能提升有很大贡献。

(2)研究优化布局对结构共振条件下应力分布情况的影响，比较了删除率为0%，50%，100%(即全铺约束阻尼结构，删除率为50%时的布局，及没有铺设约束阻尼结构)下的九宫板结构的Mises应力分布情况及其最大Mises应力值，结果表明优化布局后九宫板结构Mises应力分布影响很小，不会导致局部应力集中，但是最大Mises应力值得到有效的降低。并在优化基础上讨论了在随机激励条件下，优化后的布局可以明显降低九宫板结构中心点的加速度相应。

(3)该方法应用在复杂结构上，随着删除率增大，随着删除率的增大，敷设约束阻尼层的模态损耗因子缓慢减小，当删除率为50%时，其阻尼值下降仅仅约3%，

达到了降重的目的且阻尼性能牺牲很小，可以说明基于ESO的拓扑优化方法可以实现在较少的附加质量的情况下达到复杂结构的抑振效果，该方法可以广泛应用于一般阻尼结构的抑振优化设计，有很强的工程实用性。

[1] 姚起杭, 姚军. 工程结构的振动疲劳问题[J].应用力学学报，2006，23(1)：12-15. YAO Qihang, YAO Jun. Vibration fatigue in engineering structures [J]. Chinese Journal of Applied Mechanics, 2006，23 (1)：12-15.

[2] BERTHELOT J M, ASSARAR M, SEFRANI Y, et al. Damping analysis of composite materials and structures [J]. Composite Structures,2008, 85(3): 189-204.

[3] XIE Y M, STEVEN G P. Evolutionary structural optimization [M]. Berlin, Heidelberg, New York: Springer, 1997.

[4] 郭中泽, 陈裕泽, 邓克文, 等. 基于ESO的约束阻尼板拓扑优化设计研究[J]. 机械设计, 2006, 23(10): 3- 5. GUO Zhongze, CHEN Yuze, DENG Kewen, et al. Study on topological optimization design of constrained damping plate based on evolutionary structural optimization [J]. Journal of Machine Design,2006, 23(10): 3- 5.

[5] 郭中泽, 陈裕泽, 侯强, 等. 阻尼材料布局优化研究[J] . 兵工学报, 2007, 28(5): 638- 640. GUO Zhongze, CHEN Yuze, HOU Qiang, et al. Damping material optimal placement in damping structure design [J] . Acta Armamentarii, 2007, 28(5) :638- 640.

[6] 茅志颖,陈国平,张保强.利用拓扑优化的结构微小损伤定位研究[J].振动与冲击,2012,31(4):25-29. MAO Zhiying， CHEN Guoping， ZHANG Baoqiang. Tiny damage localization using topology optimization [J].Journal of Vibration and Shock,2012,31(4):25-29.

[7] 李超,李以农,施磊,等. 圆柱壳体阻尼材料布局拓扑优化研究[J].振动与冲击，2012,31(4):48-52. LI Chao，LI Yinong，SHI Lei, et al. Topological optimization for placement of damping material on cylindrical shells [J]. Journal of Vibration and Shock, 2012, 31(4):48-52.

[8] 柳承峰,李以农,郑玲. 约束层阻尼短圆柱壳拓扑优化分析及实验研究[J].振动与冲击,2013,32(18):49-53. LIU Chengfeng， LI Yinong， ZHENG Ling. Topology optimization and tests for a short cylindrical shell with constrained layer damping[J]. Journal of Vibration and Shock, 2013,32(18):49-53.

[9] 郑玲,谢熔炉,王宜,等.基于优化准则的约束阻尼材料优化配置[J].振动与冲击，2014,29(11):156-159. ZHENG Ling, XIE Ronglu, WANG Yi, et al. Optimal placement of constrained damping material in structures based on optimality criteria[J]. Journal of Vibration and Shock,2014, 29(11): 156-159.

[10] SIGMUND O. Numerical in stabilities in topology optimization: a survey on procedures dealing with checkerboard, mesh dependencies, local minima[J] . Structural Optimization, 1998, 16(1):68-75.

Topological optimization design of 3×3 grid stiffened panel with additional damping layers based on evolutionary structural optimization

LIU Shuangyan, LI Yulong, DENG Qiong, XU Yihang

(Fundamental Science on Aircraft Structural Mechanics and Strength Laboratory,Northwestern Poly-technical University, Xi’an 710072, China)

The topological optimization design of a 3×3 grid stiffened panel was conducted using the Evolutionary Structural Optimization (ESO) method with the amount of constrained damping layers as a constraint condition, and the maximization of modal loss factor as a target function. The optimization was completed by using a self-coded C program based on ESO method, and by applying the ABAQUS software to model the structure. The results show that along with the increase of the removal ratio of constrianed damping layers, the modal damping loss factor of the compound 3×3 grid stiffened panel remains unchanged at first, then increases to its maximum value and thereafter gradually decreases. Moreover, normalized first modal loss factor of the 3×3 grid stiffened panel with specialized additional damping layers becomes bigger and bigger, which shows that the additional damping layers in the middle portion of the panel contribute much to the suppressing of structural vibration. The Mises stress distribution contours and the maximum Mises stresses of the structures with 0%,50%,100% volume amount of constrained damping layers were compared in order to study the optimal layout of the 3×3 grid stiffened panel in resonance conditions. The results show that the optimal layout, with 50% volume amount of constrained damping layer, has little effect on the Mises stress distribution but the maximum Mises stress decreases obviously. The method has been also used in the optimization design of general complex structures to reach the aim of mass reduction with a little sacrifice in damping effect, which can be widely used in optimization design of general damping structures. The method is of great practicability.

topological optimization; sensitivity analysis; constraint damping structure

陕西省科技研究发展攻关计划(2009K01-39)；陕西省科技研究发展攻关计划(2012GY2-26)

2015-06-08 修改稿收到日期：2015-10-21

刘双燕 女，博士生，1984年生

李玉龙 男，教授，博士生导师，1961年6月生 E-mail:liyulong@nwpu.edu.cn

O327；O342

A

10.13465/j.cnki.jvs.2016.22.029