基于离散呼吸子理论的靶能量传递研究

李海勤， 孔宪仁, 叶 东， 刘 萌

(哈尔滨工业大学 卫星技术研究所，哈尔滨 150001)



基于离散呼吸子理论的靶能量传递研究

李海勤， 孔宪仁, 叶 东， 刘 萌

(哈尔滨工业大学 卫星技术研究所，哈尔滨 150001)

研究了一个具有非线性能量阱的两自由度线性振子耦合系统，确定了其产生靶能量传递的条件和传递频率。建立了无量纲形式的振动方程，利用复变量——平均法推导了保守系统的慢变动力流和哈密顿函数。基于哈密顿力学和相空间中的离散呼吸子理论确定了系统产生靶能量传递的质量比条件和初值条件，并采用椭圆积分计算得到靶能量传递的频率。通过数值仿真验证了有阻尼系统中靶能量传递的不可逆性。

非线性能量阱；靶能量传递；哈密顿力学；自由振动；离散呼吸子

在线性振子之间，能量的传递是依靠共振来实现的，当发生共振时能量在两振子之间以特定的频率完全传递，循环往复。而非线性系统中，振动频率和幅值的独立性被打破，即系统的振动频率依赖于振动幅值[1]。因此非线性振子间的能量传递机制要复杂得多，是非线性振动研究的一个主要方面。

早期研究集中于周期解，并指出非线性主要起着两个作用[2-4]：一是通过适当的调节非线性振子的幅度，非线性可以恢复非线性振子之间的共振，而线性系统将不会出现这种情况；二是对于不同幅度的非线性振子，非线性可以有效避免其它模态下局部共振的出现。因此，系统也可以保持准确的局部模态，而且，这些模态的存在并不依赖于随机性。这些模态就被称之为离散呼吸子[5-6](Discrete Breather，DB)。

离散呼吸子又被称作局部化模态，指的是离散非线性动力系统中的局部周期解。BALTZ等[7]在其研究中提到的极子的概念实际上就属于DB的范畴。在化学领域，对于小分子情况，也很早就有了DB的概念，且这种形式的解被人们公认为对于理解量子化的分子振动至关重要。SIEVERS等在近似的解析分析和数值计算的基础上首次指出在一般模型中存在DB形式的长期周期解，后来，人们通过严格的证明指出Klein-Gordon系统中存在DB形式的准确解，并给出了DB存在的两个必要条件：非线性和离散性。另外，DB还被证明具有很好的鲁棒性。

KOPDAKIS等研究非线性系统的DB之间的能量传递机理时发现了能量在DB之间的一种高效传递的现象[8]。他们指出在DB中存在着高效选择性强的能量单向传递现象，并称之为靶能量传递[9](Targeted Energy Transfer，TET)。他们考虑一个由源系统和受体系统两个子系统组成的动力系统，当TET发生时，能量由源系统完全传递至受体系统，由于该能量传递对初始条件的选择性和阻尼耗散的原因，能量无法在回到源系统，从而实现能量单向传递。TET现象虽然是在研究DB时被提出的，但是普遍性比DB要更广，因此的到了广泛的关注，并被引用到各个领域。靶能量传递通过共振俘获现象实现，当一个系统满足特定的初始条件，其相轨迹被吸引到共振流形[10]，若一段时间后系统的轨迹会逃逸出共振流形则称为瞬态共振俘获，否则称为持续共振俘获。在共振俘获现象发生时，特定的能量在非线性系统之间相互交换，被称为靶能量传递现象。

将TET现象应用到振动控制中，是通过非线性能量阱实现的。对于一个非线性设备，把它连接到一个基础结构并实现能量到该设备的局部化，称为非线性能量阱[11](Nonlinear Energy Sink，NES)。一个NES通常需要两个部分：一个非线性刚度和一个阻尼(通常为线性粘性阻尼)。前者用来使NES与基础结构的任一线性模态实现共振，而后者则用来耗散掉通过共振传递到NES中的振动能量。目前对NES的研究表明至少存在三种不同的TET机制，通过1∶1共振、亚谐共振、以及非线性拍现象。其中主结构和NES之间频率比为1∶1的同步振动是产生TET的主要机制，系统的轨迹被吸引到1∶1共振流形，能量快速从主结构传递至NES，由于阻尼作用，系统的振动能量将一直减少，系统不断从一个共振状态逃逸并被俘获到另一个新的状态，直至系统不再具有发生共振俘获的条件，共振俘获结束，并打破了主结构同吸振器之间高效传递能量的条件，系统达成一次靶能量传递。

本文研究带有非线性能量阱的两自由度系统，确定产生靶能量传递的条件和靶能量传递的频率。

1 系统模型

1.1 研究对象

研究如图1所示的两自由度非线性系统，由一个接地线性主结构耦合一NES组成。图中k1为线性刚度，m1为主结构质量，m2为NES质量，且满足m1≪m2，c为线性阻尼，k2为非线性刚度，其受力和位移的关系为F=k2x3。

图1 系统模型Fig.1 Model of system

设主结构和NES的位移分别为x1,x2，则有系统的动力学方程为:

(1)

作变量替换:

不妨令ω=1，并将式(2)代入到式(1)中，可得到无量纲形式的运动方程如下：

(3)

其对应保守系统为:

(4)

1.2 慢变动力流

动力流自然的出现在上述自治系统中，可采用Manevitch等人提出的复变量-平均法[12]来推导。复变量—平均法的建模分为复变量过程和平均化过程两大步。将式(4)的运动分为质心运动和相对运动两部分:

u=x1+εx2, v=x1-x2

(5)

并采用复变量处理，

(6)

上式基于1∶1内共振的情形，将系统的周期解表示成角频率与主结构固有频率相同的快速振动部分eit和振动幅值的慢变调制部分φi(t)两部分。分别对应于系统的动力学的快变部分和慢变部分得如下形式的复变量方程:

(7)

研究其慢变部分，对快变部分进行平均化处理，e-2it，e-4it，e2it在一个周期内均值都为零，于是得到：

(8)

上式即为系统的慢变动力流。选取参数为ε=0.05，k=20，初始能量E=0.082，对比式(4)和式(8)的模型得到图 2。

图2 系统对比Fig.2 Comparison of system

可知，慢变流对于主结构的运动有很好的近似效果，而对于NES振子的近似效果虽然没由主结构好，但是研究每个周期的平均结果仍然可以取得很好的结果，故可以采用慢变流来对系统进行近似分析。

2 靶能量传递

2.1 哈密顿函数

式(8)的慢变流经过如下正则变换，

(9)

可以得到式(8)的哈密顿函数为:

(10)

并满足哈密顿方程:

(11)

另一方面，可以将式(8)写成下述形式:

(12)

取其共轭式并联立可得另一个不变量，

(13)

2.2 靶能量传递条件

下面根据离散呼吸子理论研究两振子间能量传递规律，定义新的正则坐标为(I1,θ1)，(I2,θ2)将系统的运动表示成极坐标形式，具体关系为:

(14)

由式(10)所确定的系统哈密顿量具有如下的等价形式:

H=H0(I0,I)+V(I0,I,θ)

(15)

其中,

并且，可知(I0,θ0),(I,θ)也是哈密顿系统的一组共轭坐标对。式(15)中H0(I0,I)和V(I0,I,θ)分别为:

(17)

其中,

(18)

相空间中，系统的总能量ET和总路径IT守恒，分别对应与前面的两个积分不变量，即:

IT=I1+I2=2I0=Z,ET=H

(19)

假定在初始时刻能量完全集中在供体系统，对应的初始条件为:

I1(0)=2I0≠0,I2(0)=0

(20)

经过一段时间tT后，能量完全传递至受体系统：

I1(tT)=0,I2(tT)=I1(0)=2I0

(21)

并结合式(16)，可知在能量完全传递时I的变化为I(0)=I0,I(tT)=-I0，当该关系满足时，称此时的能量传递的能量传递为靶能量传递(Targeted Energy Transfer,TET)。发生靶能量传递时，I遍历整个-I0到I0的整个区间，或者说系统的轨迹经过二维球面相空间(I,θ)的两个极点。更进一步地，在极点处的能量相等，根据式(15)和式(17)，有:

H0(I0,I0)=H0(I0,-I0)=E

(22)

解上述方程，可以得到引发靶能量传递的条件时，系统的总相径和总能量满足如下关系:

(23)

式(23)即为产生靶能量传递的初始条件。

另外，相空间的闭合轨道可以由如下方程描述:

V(I0,I,θ)=H0(I0,±I0)-H0(I0,I)=Δ(I)

(24)

式中：Δ(I)表征了能量在供体系统和受体系统的调谐，系统轨迹能够经过相空间两个极点的充要条件是:

(25)

联立式(17)、式(24)和式(25)，得:

(26)

上式对所有的I都成立，当满足:

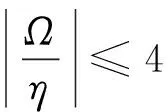
(27)

式(27)和式(23)共同给出了产生靶能量传递的基本条件。式(27)表明，只有当质量比ε≥0.056时能量才能实现完全传递，并称ε=0.056为临界质量比。图3给出了在质量比条件满足的情况下，不同初始条件的相轨迹。当初值条件满足式(23)时，对应于图3(b)所示，系统初始能量全部集中在供体系统，经过一个周期，系统相轨迹的I遍历[-I0,I0]，相角在0到2π的某个子区间内变化，能量可以完全地由供体系统传递至受体系统，而图3(a)和图3(c)均不满足初始条件式(23)故无法实现靶能量传递。图 4中质量比条件不满足式(27)所给定，此时系统相轨迹在I=0时出现“断裂”，其结果是I无法穿越零点，而相角θ遍历整个区间0到2π。能量无法完全传递，即使初始条件满足式(23)，也无法实现靶能量传递。但是当初始时刻能量不完全集中在供体系统，对应于零时刻I略小于I0的情况，可以避免在零点的相轨迹断裂，实现较高传递效率。

图3 不同初始条件下的相轨迹Fig.3 Phase portrait for system with different initial condition

图4 不同质量比下的相轨迹Fig.4 Phase portrait for system with different mass index

数值结果如图5所示，假定初始时刻能量全部集中于主结构，初值条件均按照式(23)给定，能量传递效率用R来描述(NES的最大能量和总能量之比)。在图5(a)中，质量比ε=0.05小于临界质量比，图5(b)中ε=0.056，等于临界质量比，图5(c)中ε=0.1，大于临界质量比。综合图5(a)、(b)、(c)三个子图，亦可发现在质量比大于临界质量时才能实现能量完全传递，质量比小于临界质量时，只有很小一部分能量传递至NES。

在图5(d)、(e)、(f)中，改变了质量比参数ε和刚度k的值，比较图5(c)、(e)、(f)可以发现增大质量比ε，在规定时间内两振子之间的能量交换次数也增加，即靶能量传递的频率增大，对比图5(c)、(d)可以发现，在ε相等而k不相等的情况下，传递的频率几乎不变。

为了确切求得靶能量传递的频率，并确定其和系统各个参数之间的关系，首先列出哈密顿方程如下:

(28)

结合上式，联立式(15)、式(17)和式(28)式，消除θ项，得:

(29)

其中,

(30)

另一方面，当能量完全传递时，式(23)的条件满足。将式(23)代入到式(30)，得到:

(31)

在式(31)的条件下，式(29)的解为雅克比椭圆余弦：

(32)

这也要求:

(33)

成立，此结果和式(27)所要求的一样。根据式(33)，可以得到靶能量传递的频率为:

(34)

式中，K(l)为第一类椭圆积分。

由于上式中l,η都只和质量比ε有关，因此靶能量传递的频率由质量比ε唯一确定，而与刚度的选取无关，这一结果与前面数值结果相符合。

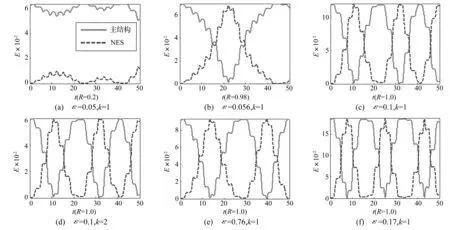
图5 数值结果Fig.5 Numrical results

3 有阻尼系统数值仿真

对有阻尼系统，确定两振子之间的能量传递规律。以初始时刻能量全部集中在主结构的情形，分别取ε=0.1,k=1,初始能量按照式(23)给定。分别取λ=0.06、λ=0.1和λ=0.2，得图6。在图6(a)中，初始时刻能量从主结构传递到NES，由于阻尼的存在，这部分能量不能再返回主结构进行下一次交换，而是被消耗掉，在一段时间内，两振子之间一直保持较高效率的能量传递，但由于阻尼较小，总能量耗散的速度不够快，减振效果并不明显。当阻尼增大到图6(b)所示时，在经过两次能量交换后，系统能量迅速降低，此后能量主要集中在主结构中，两振子之间的靶能量传递被打破，总能量维持在一个较低的水平，达到较好的减振效果。当阻尼进一步增大，如图6(c)所示，虽然在初始时刻，部分能量传递到NES被阻尼消耗，但经过一次不完全的能量传递，能量便无法由主结构向NES传递，靶能量传递被过早的打破，能量几乎完全集中在主结构中，减振效果反而降低。总的来说，随着阻尼的增大，整个系统的减振效果先变好后变差。

阻尼在系统能量耗散的过程中起着双重作用，一方面，它消耗了由主结构传递到NES的能量，使其不能再回到主结构，主结构的能量被大幅降低。另一方面，由于阻尼的出现，系统出现对称破缺，两振子之间传递的对称性被打破，能量从主结构的NES单向传递，表现出不可逆性。增大阻尼加快了能量的消耗，但也更快的打破两振子之间的靶能量传递条件。故选择阻尼比的时候要综合考虑这两个作用的影响，并不是越大越好。应合理选取吸振器的阻尼。

通过多次选取阻尼进行数值仿真可确定最优阻尼约为子图6(b)中的λ=0.1。而对于阻尼的对系统影响的解析描述和最优阻尼的理论验证则有待进一步研究。

图6 有阻尼系统Fig.6 Damped system

4 结 论

本文研究了非线性耦合振子之间的产生靶能量传递的条件和靶能量传递的频率。利用复变量平均法推导了系统的近似慢变流，基于哈密顿函数和相平面法得出了能量在线性振子和NES之间完全传递的两个条件：分别为质量比条件和初始能量条件。并利用椭圆函数计算了靶能量传递的频率的准确值，结果表明靶能量传递的频率由质量比唯一确定，与非线性刚度无关，并且质量比越大，靶能量传递越快。最后，通过数值仿真，研究了弱阻尼系统的能量传递现象，表现出不可逆性，且阻尼比不是越大越好，存在最优阻尼比以达到最优减振效果。

[1] PEETERS M, VIGUIÉ R, SÉRANDOUR G, et al. Nonlinear normal modes, part II: toward a practical computation using numerical continuation techniques[C]// 26th International Modal Analysis Conference,2008:1-22.

[2] AUBRY S, KOPIDAKIS G, MORGANTE A M, et al. Analytic conditions for targeted energy transfer between nonlinear oscillators or discrete breathers [J]. Physica B Condensed Matter, 2001, 296(1/2/3):222-236.

[3] KOPIDAKIS G, AUBRY S. Intraband discrete breathers in disordered nonlinear systems. I. Delocalization[J]. Physica D Nonlinear Phenomena, 1999, 130(3/4):155-186.

[4] KOPIDAKIS G, AUBRY S. Intraband discrete breathers in disordered nonlinear systems. II. localization[J]. Physica D Nonlinear Phenomena, 2000, 139(3/4):247-275.

[5] SIEVERS A J, TAKENO S. Intrinsic localized modes in anharmonic crystals[J]. Physical Review Letters, 1988, 61(8):970-973.

[6] CAMPBELL D K, PEYRARD M, CAMPBELL D K. Chaos-soviet american perspectives on nonlinear science[C]//American Institute of Physics Maryland:AIP, 1990:24-115.

[7] BALTZ R V, BIRKHOLZ U. Polaronen[M].Berlin: Springer, 1972:233-341.

[8] 张也弛，孔宪仁，张红亮. 非线性耦合振子间的靶能量传递研究:保守系统中的完全能量传递[J]. 振动与冲击, 2012, 31(2):150-155. ZHANG Yechi，KONG Xianren，ZHANG Hongliang. Targeted energy transfer among coupled nonlinear oscillators: complete energy exchange in a conservative system[J].Journal of Vibration and Shock, 2012, 31(2):150-155.

[9] KOPIDAKIS G, AUBRY S, TSIRONIS G. Targeted energy transfer through discrete breathers in nonlinear systems[J]. Physical Review Letters, 2001, 87(16):175-196.

[10] COLVIN M C. Energy sinks with nonlinear stiffness and nonlinear damping [D]. Maryland:University of Maryland, 2010:1-31.

[11] LEE Y S, VAKAKIS A F, BERGMAN L A, et al. Passive non-linear targeted energy transfer and its applications to vibration absorption: a review[J]. Institution of Mechanical Engineers, 2008, 222: 77-134.

[12] MANEVITCH L I, MUSIENKO A I, LAMARQUE C. New analytical approach to energy pumping problem in strongly nonhomo-geneous 2-DOF systems[J]. Meccanica, 2007, 42(1): 77-83.

Investigation on targeted energy transfer based on discrete breather theory

LI Haiqin, KONG Xianren, YE Dong, LIU Meng

(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150001, China)

Analytic conditions and transmitting frequency for targeted energy transfer were investigated on a 2-dof system comprising of a linear oscillator coupled with a nonlinear energy sink. The vibration equations were formulated in a dimensionless form, then the dynamic flow and Hamiltonian function for the underlined conservative system were derived by the complex-averaging method. Based on the Hamiltonian and discrete breather theory in phase space dynamics, the mass ratio and initial value condition linked to a complete energy transfer in the conservative system were determined, and the frequency of the targeted transfer was calculated by the Jacobian elliptic integral. As a result of numerical simulation, the irreversibility of targeted energy transfer in damped system was demonstrated.

nonlinear energy sink; targeted energy transfer; Hamiltonian mechanics; free vibration; discrete breather

微小型航天器系统技术(IRT0520)

2015-06-12 修改稿收到日期：2015-11-08

李海勤 男，硕士生，1992年生

孔宪仁 男，博士生导师，1961年生

O328;O322

A

10.13465/j.cnki.jvs.2016.22.014