中心商同构于p6阶第十九家族的一类LA-群

陈科成, 班桂宁, 聂婷婷

(广西大学 数学与信息科学学院,南宁 530004)



中心商同构于p6阶第十九家族的一类LA-群

陈科成, 班桂宁, 聂婷婷

(广西大学 数学与信息科学学院,南宁 530004)

基于Rodney James的p6阶群的完全同构分类理论, 继续LA-群的研究工作。利用群的扩张理论与自由群理论，得到一类中心非循环且中心商同构与Φ19(16)的有限p-群，最后运用自同构的性质证明了此类群是LA-群。

有限p-群;群的扩张;LA-群;自由群

群论孕育至今极大地推动了数学的发展,有限p-群是其最重要的分支之一。把满足|G||Aut(G)且|G|=pn,n>2的有限非循环p -群定义为LA-群。在LA-群及有限p-群自同构上班桂宁等获得到了一些有价值的成果[1-9]。 崔艳证明中心商同构于Φ19(16)的一类群是LA-群[10],但其中心Z(G)是循环群。本研究结合James关于p6阶群的分类[11], 证明了Z(G)是非循环群的限定条件, 并证明了在此条件下这类群是LA-群。

1 理论基础

1.1 相关定义

定义1[12]30设G是有限群, ∀a,b∈G, 规定[a,b]=a-1b-1ab,叫作元素a,b的换位子, 再令G′=〈[a,b]|a,b∈G〉, 称为G的换位子群或导群。 此外, 规定G(0)=G, G(n)=(G(n-1))′,n≥1, 称G(n)为G的n阶换位子群。

下文群的定义关系中, 形如[ai,aj]=1,(i,j=1,2,…,n)的略去不写。

定义2[12]139设G是有限群。若G≠1, 令Φ(G)为G的所有极大子群的交; 而若G=1,Φ(G)=1, 称Φ(G)为G的Frattini子群。

定义3[13]121设G是群,a,b∈G,i,j为正整数,规定:

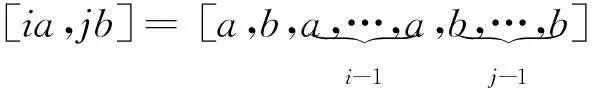
定义4[14]若群G是非交换且没有非平凡交换直积因子的p -群, 则称群G是PN-群。

本研究所用的群论符号或基础定义皆可参考文献[7]。

1.2 主要引理

引理1[12]130设G是群,a,b,c∈G, 则

1)ab=a[a,b];

2)[a,b]c=[ac,bc];

3)[a,b]-1=[b,a]=[a,b-1]b=[a-1,b]a;

4)[ab,c]=[a,c]b[b,c];

5)[a,bc]=[a,c][a,b]c。

引理2[13]123设G是群, a,b∈G且[a,b]∈Z(G), 又设n是正整数，则有

1)[an,b]=[a,b]n，[a,bn]=[a,b]n;

2)(ab)n=anbn[b,a]；

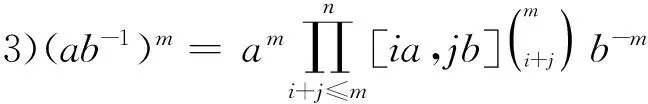
引理3[13]121设G是亚交换群,a,b∈G, 设m,n是正整数, 则

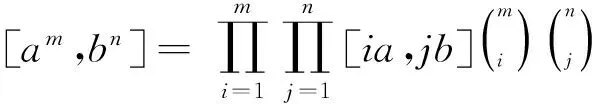
下文提到的schreier扩张只是表示这种循环扩张。

引理5[15]对于群G=〈a1,a2,…,ar|fi(a1,a2,…,ar)=1,i∈I〉。

1) 如果σ∈Aut(G), 并且∀i∈I,fi(σ(a1),σ(a2),…,σ(ar))=1;

如果|G|≤|H|<+∞, 则上述σ为群同构(即H是由生成元{a1,a2,…,ar}与定义关系fi(a1,a2,…,ar)=1,∀i∈I所定义的群)。

引理7[17]若G是PN-群, 则R(G)=Ac(G)Inn(G)为p -群。

引理8[18]若G是PN-群, 则|R(G)|=|G/Z2(G)|·|Ac(G)|。

设G是有限群, N≤G, AN(G)={σ|g-1gσ∈N,σ∈Aut(G)}, 则AN(G)≤Aut(G), 称AN(G)是群G的N-自同构。特别地, 记Ac(G)=AZ(G)(G)。

引理9 如果Z(G)≤Φ(G), 那么G为PN-群。

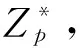
2 主要定理及证明

2.1 定理1的证明

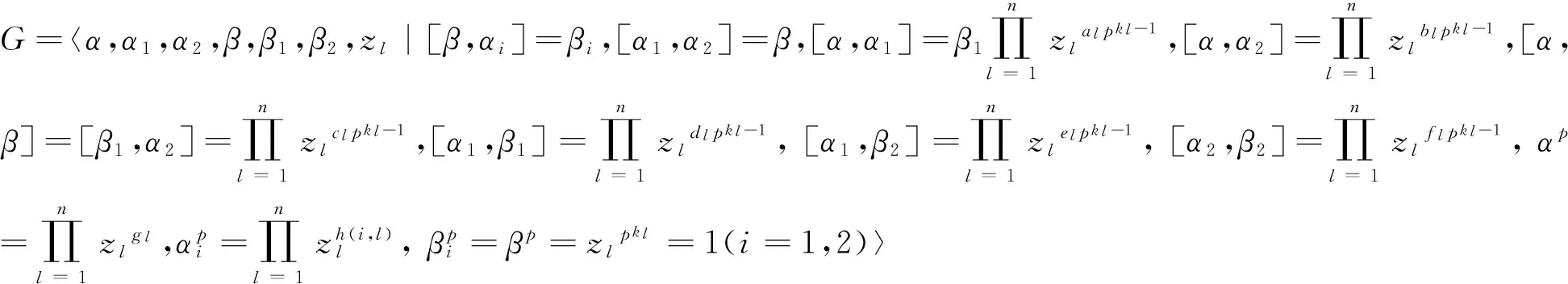
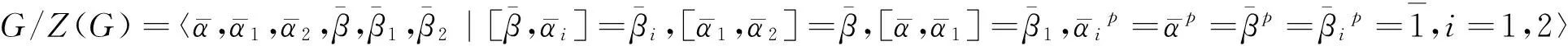
通过换位子的运算有[α,α2],[α,β]∈Z(G)，所以[α,α2]=[α,α2]β,[α,β]=[α,β]α1, 得到[α,β2]=[α,β1]=1。这些为1的换位子可以省略, 不出现在G的群结构中。

因为[α,α2]=[α,α2]α1=[αβ1,α2β-1],所以[α,β-1][β1,β-1][β1,α2]=1；因为[β1,β-1]=1，得到[α,β-1][β1,α2]=1，即[β1,α2]=[β-1,α]；因为[β1,α2]∈Z(G),所以[β1,α2]β=[β,α2],由引理1得[β-1,α]β=[α,β]，从而得[β1,α2]=[α,β]。

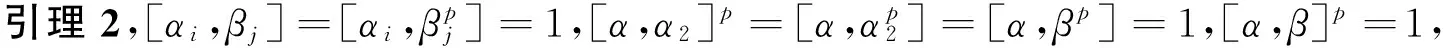
第二步，做三次扩张。

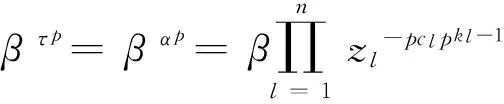
现证明扩张得到的G(1)与1)中给出的定义关系一致。

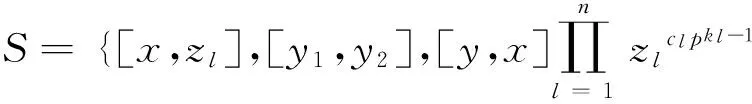
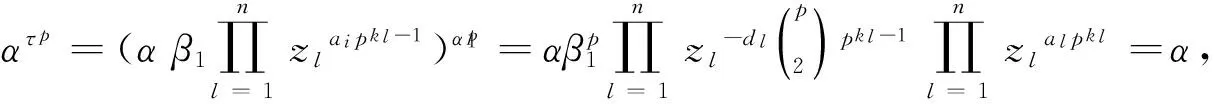
现证明扩张得到的G(2)与2)中给出的定义关系一致。

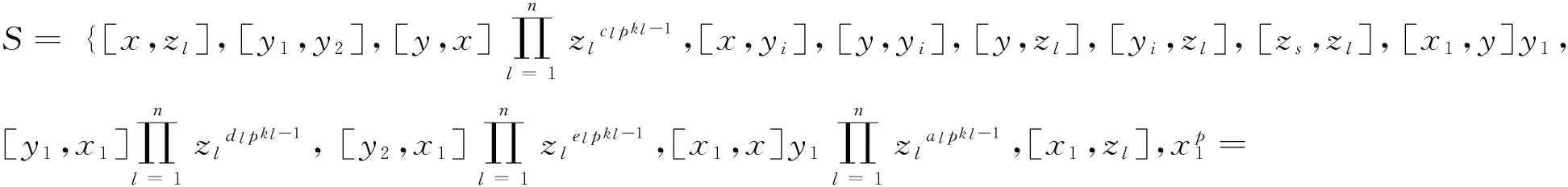
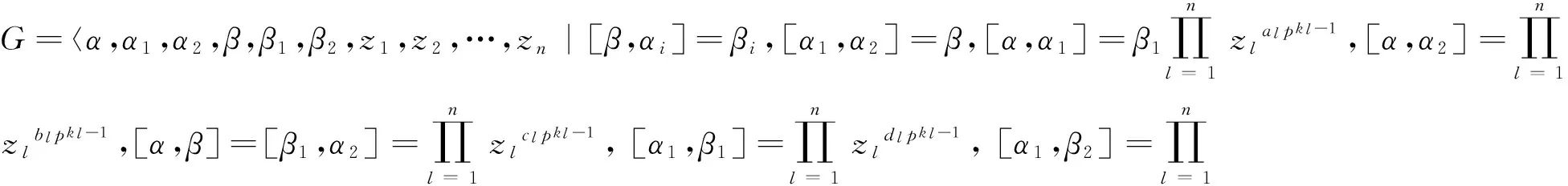
令N=G(2)如上文所得，设F=〈s3〉为p循环群, 构造群N到N的映射τ:

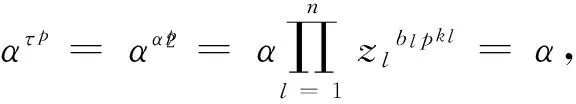
现证明扩张得到的G与3)中给出的定义关系一致。

综上三步证明了定理1。

2.2 定理2的证明

定理2 定理1中所得的群G是LA-群。

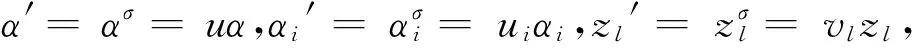
群G的一个自同构群R(G),由引理7和引理8可知, |R(G)|=|G/Z2(G)|·|Ac(G)|, 从而logp|R(G)|≥4+2n+logp|Z(G)|。因为logp|G|=6+logp|Z(G)|, 所以当n≥2时, 有logp|R(G)|≥logp|G|, 即|G|||Aut(G)|, 从而此时G是LA-群。当n=1时，logp|R(G)|≥6+logp|Z(G)|≥logp|G|, 综上得G是LA-群。

[1] BAN G, ZHANG J, YU S X. The lower bound for the order of the automorphism groups[J].Proceedings of the Royal Irish Academy, 1996, 96A(2): 159.

[2] 班桂宁，陈立英，周宇.一系列新的LA-群(英文)[J]. 广西师范学院学报(自然科学版),2007, 24(4): 5.

[3] SHABANI-ATTAR M.On equality of order of a finitep-group and order of its automorphism group[J]. Bulletin of the Malaysian Mathematical Sciences Society, 2015，38(2):461.

[4] 班桂宁, 刘海林, 崔艳. 中心循环且中心商群的阶为p6的LA-群[J].重庆理工大学学报(自然科学), 2014, 28(1): 120.

[5] 钟祥贵.一类有限群的自同构群阶的上确界[J].广西科学,2002,9(1):16.

[6] 张中健，班桂宁，戴琳.一类特殊p-群的自同构的阶[J]. 云南民族大学学报(自然科学版),2011, 20(1): 37.

[7] 班桂宁,许永峰,陈倩,等.一类中心商同构于第四十家族的LA-群[J].贵州大学学报(自然科学版), 2015, 32(1): 1.

[8] 田甜.非循环中心商群同构于若干阶族群的LA-群[D].南宁:广西大学, 2016.

[9] 班桂宁,周宇,陈立英.一类特殊p-群自同构群的结构[J].郑州大学学报(理学版),2008, 40(1): 52.

[10] 崔艳.若干中心是循环的LA-群[D]. 南宁: 广西大学, 2014.

[11] JAMES R. The groups of orderp6(pan odd prime)[J]. Mathematics of Computation, 1980, 34: 630.

[12] 徐明曜. 有限群导引(上)[M].2版.北京: 科学出版社, 2001.

[13] 徐明曜. 有限群导引(下)[M].2版.北京: 科学出版社, 2001.

[14] EXARCHAKOS T. LA-groups[J]. Journal of the Mathematical Society of Japan, 1981, 33(2): 185.

[15] 班桂宁, 俞曙霞. 交换自同构群的一个重要结论[J]. 中国科学(A辑), 1996, 26(12):1072.

[16] 班桂宁, 俞曙霞. 一类p-群的自同构群的阶[J].数学学报, 1992, 35(4): 570.

[17] OTTO A D. Central automorphisms of a finitep-group[J]. Transactions of the American Mathematical Society,1966,125(2):282.

[18] 许永峰. 一类中心非循环且中心商群的阶为p6的LA-群[D]. 南宁: 广西大学, 2015:10.

A class of LA-groups with central quotients being isomorphic to the order ofp6-group of nineteenth family

CHEN Kecheng,BAN Guining,NIE Tingting

(School of Mathematics and Information Sciences, Guangxi University, Nanning 530004, China)

Based on the complete isomorphism classification theory of Rodney James’s groups of orderp6, we continue to study the LA-group. By using the extension theory of group and the theory of free group, we get a new series of finitep-groups with central non-cyclic and quotients being isomorphic to the group of Φ19(16). Eventually we prove that the groups are new LA-groups by the characteristic of their automorphisms.

finitep-group; extension theory of group; LA-group; free group

10.3969/j.issn.1671-8798.2016.05.001

2016-07-21

陈科成(1990— ),男, 浙江省宁波人,硕士研究生, 研究方向为基础数学的有限群论。

O152.1

A

1671-8798(2016)05-0337-07