指挥台围壳雷达隐身性数值模拟
2016-12-12薛丰利黄沛霖罗蒙浩姬金祖
薛丰利,黄沛霖,罗蒙浩,姬金祖
北京航空航天大学航空科学与工程学院,北京100191
指挥台围壳雷达隐身性数值模拟
薛丰利,黄沛霖,罗蒙浩,姬金祖
北京航空航天大学航空科学与工程学院,北京100191
对潜艇指挥台围壳在水面航行状态和半潜航行状态下的雷达隐身性进行研究。基于高频法,应用CATIA和MATLAB软件对三元流线型指挥台围壳和传统的直壁式指挥台围壳的雷达散射截面积(RCS)特性进行数值模拟和对比分析,并在此基础上进行雷达发现概率的计算。研究指挥台围壳的探测概率随距离变化的关系和指挥台围壳在2种航行状态下各重点探测角域探测概率的变化关系。研究表明,对指挥台围壳进行三元流线型设计并配合低矮化设计后,能明显改善潜艇指挥台围壳的雷达隐身性。
指挥台围壳;雷达散射截面积;隐身;高频法;探测概率
0 引 言
潜艇的隐蔽性是其赖以生存的重要条件。当潜艇处于工作深度潜行状态时,声探测是最有效的探测手段,对潜艇的隐身性能改进也多集中于声隐身。但大多数潜艇,尤其是常规潜艇经常需要定期浮出水面充电和换气;潜艇在潜望深度航行时,其潜望镜、通气浮阀等装置经常处于暴露状态,又由于这些设备多呈圆柱形,在雷达荧光屏上将出现稳而亮的显示。可见,雷达仍是探测潜艇的重要手段之一,仍需考虑其雷达隐身性。
指挥台围壳是潜艇的标志性结构,用于围封
耐压指挥或设闸室和各种升降装置等,也是现代潜艇执行水面航行、收发信息、靠离码头、实施观测和指挥的重要部位[1]。当潜艇处于水面航行状态或半潜航行状态时,指挥台围壳会给雷达探测提供明显的信号。因此,需要对指挥台围壳进行改进设计。
传统的潜艇指挥台围壳多为直壁式设计,且比较高,针对此类指挥台围壳的特性研究也已较为充分。胡其望[2]以指挥台围壳缩比模型为研究对象,对潜艇指挥台围壳噪声产生的机理、特性、评价方法以及低噪声设计技术进行了分析。吴方良等[3]采用雷诺平均Navier-Stokes(RANS)方法计算潜艇的三维粘性流场,分析了指挥台围壳大小和相对潜艇的位置对潜艇水动力性能的影响。
20世纪60年代以来,逐渐出现了一些指挥台围壳外形低矮且具有极好流线型的潜艇,较为典型的有德国的212型、瑞典的2000型,以及前苏联的“阿库拉”级核潜艇。国内、外已针对此类新型三维围壳开展了较多相关的研究。Gorski等[4]对新型的三维指挥台围壳进行设计和研究,并对其流场进行了风洞试验测试。王志博等[5]对三维围壳进行数值计算,比较了不同三维围壳对尾流场的影响,并从多个侧面分析了围壳外形与潜艇尾流场特征的关系。刘龙举等[6]分析了三维的沙丘形围壳对阻力和尾流场的影响,验证了可以通过改变指挥台围壳形状达到减阻和均匀尾流场的目的。
尽管对传统的直壁式指挥台围壳和新型的三维围壳都已经开展了充分的研究,但内容多集中于指挥台围壳对潜艇流场性能的影响,而有关潜艇指挥台围壳雷达隐身性方面的研究则较少。本文将以直立式翼型围壳和三维围壳为对象,通过数值模拟计算,比较不同围壳外形对雷达隐身性的影响。
1 理论依据
本文的理论依据主要包括RCS高频计算方法和雷达探测概率模型。
1.1 RCS高频计算方法
本文采用高频法计算RCS,具体采用物理光学法计算面元散射[7-9],采用等效电磁流法计算边缘绕射,并考虑多次反射及遮挡判断[7-8]。
物理光学法计算面元散射的公式如下:

等效电磁流法是将Keller椎上的绕射贡献等效为棱边上的电流和磁流,然后再进行计算。
在本文中,考虑多次反射主要是针对理想导体的二次反射情况,采用射线追踪法。
遮挡判断分明暗面判断与面元判断2种。明暗面的判断采用将入射方向与面元的法向进行相乘,即计算,则此面元为暗面,反之为亮面。面元遮挡采用的方法为:当某面元的中心被另一个面元遮挡时,就认为此面元被遮挡。
1.2 指挥台围壳被雷达探测的概率模型
雷达在某探测方向上的最大探测距离为

式中:Pt为雷达的发射功率,W;G为雷达天线的增益,dB;λ为雷达所用波长,m;σ为目标的雷达散射截面积,m2;k为玻尔兹曼常数,k=1.38×10-23J/K;T0为标准室温,T0=290 K;Bn为噪声带宽,Hz;Fn为噪声系数,dB;D0为最小可检测信噪比,dB。

2 指挥台围壳的RCS数值模拟
岳奎志等[11]对挂载导弹的作战飞机系统的RCS特性进行了研究,并给出了RCS数值模拟流程,参照此流程,指挥台围壳的RCS数值模拟将包括模型建立、模型的RCS数值模拟以及雷达探测概率对比3个部分。
2.1 指挥台围壳模型绘制
本文指挥台围壳模型参考SUBOFF潜艇和“阿库拉”潜艇,利用CATIA软件绘制外形并生成网格。模型1参照SUBOFF潜艇,采用直立式翼型;模型2参照“阿库拉”潜艇,采用三元流线型,
即指挥台围壳沿着XY剖面、XZ剖面、YZ剖面均呈现为光滑的流线状。模型1和模型2的三维示意图分别如图1和图2所示。

图1 模型1示意图Fig.1 The diagrammatic sketch of model 1

图2 模型2示意图Fig.2 The diagrammatic sketch of model 2
为了使对比结果具有代表性,两个模型的长度l、最大厚度b,以及高度h保持一致,具体数值如下:l=14 m,b=3 m,h=4 m。
2.2 指挥台围壳模型的RCS数值模拟
通过MATLAB软件,基于物理光学法和等效电磁流法,对上文中所生成的网格进行数值模拟,计算时需要考虑二次反射和遮挡。一般认为,舰艇“雷达威胁区域”在水平面内方位角范围为0°~360°,在垂直面内仰角范围限定在0°~20°[12]。参照各国海军机载雷达的情况[13],发现海军机载雷达所用频段多为X波段(8~12 GHz)。模拟雷达波入射时,选取X波段频率的中间值10 GHz进行计算,方位角选取0°~360°,俯仰角0°~20°,角度的间隔为1°。又考虑到垂直极化下海平面散射的贡献很大[14],所以模拟过程中选取水平极化HH。
为便于比较和减少计算复杂度,本文仅考虑指挥台围壳本身对隐身性的影响,不考虑海平面的背景噪声,也不考虑指挥台围壳与艇体之间的相互作用。计算所得各俯仰角下的RCS均值如图3所示。

图3 指挥台围壳位于水面航态时随俯仰角变化时的RCS均值曲线Fig.3 RCS values of the sails on the water at different elevations
由图3可知,当潜艇处于水面航行状态时,在俯仰角2°以内,模型2的RCS均值明显小于模型1;当俯仰角>2°时,模型2的RCS均值又明显大于模型2,但模型2的RCS均值整体上基本能维持在0 dBsm以下,而模型1在0°时其RCS均值高达15 dBsm以上。对图3中的单位进行换算后,得到在俯仰角0°时,模型2的不足模型1的1%;在俯仰角>5°时,模型2的在模型1的50倍以上;而当俯仰角>10°时,模型2的在模型1的100倍以上。
然后,再对潜艇处于半潜航行的状态进行数值模拟,分别截取模型1和模型2的上半部分,用与上文相同的方式计算,得到半潜航行状态下各俯仰角的RCS均值如图4所示。

图4 指挥台围壳位于半潜航态时随俯仰角变化的RCS均值曲线Fig.4 RCS values of the sails underwater at different elevations
由图4可知,当潜艇处于半潜航行状态时,在俯仰角较小的情况下,模型2的RCS均值小于模型1的,而随着俯仰角的增大,模型2的RCS均值逐渐大于模型1的,两条曲线趋势与潜艇处于水面航态时的情况类似,模型1呈现波动状的下降趋势,模型2呈现稳步上升趋势。但在半潜航态下,模型2的RCS均值小于模型1的RCS均值的角域范围增大了,由0°~2°增大到了0°~5°。
由于模拟半潜航行状态时是通过直接截取水面航行状态模型的上半部分,截取前、后的模型形状相似,只是高度发生了变化,因此半潜航态的模型亦可视作低矮化设计后的水面航态的模型。对图3、图4中的单位进行换算,计算得到在俯仰角0°时模型1半潜航态下的为水面航态下的39.8%,模型2半潜航态下的为水面航态下的44.7%;但在俯仰角5°及以上时,模型1在半潜航态下的维持在水面航态下的90%以上,而模型2半潜航态下的则维持在水面航态下的30%以内。可以看出,对三元流线型的潜艇进行低矮化设计后,RCS的降低效果非常明显。
由于在实际应用中,雷达波对水面舰艇的最大威胁方向在竖直方向局限在很小的仰角范围θ内,一般不超过4°,而对水平方位角φ而言,每个角度的威胁是等同的[12]。所以,评价指挥台围壳的隐身性能时,应重点考虑俯仰角0°~4°时的情况,此俯仰角范围内的部分水面航态RCS特性曲线如图5~图7所示。

图5 水面航态下俯仰角0°时RCS曲线Fig.5 RCS values of the sails on the water at 0°
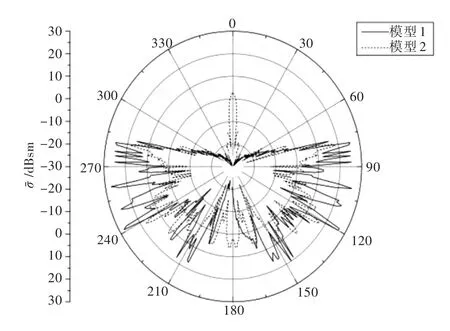
图6 水面航态下俯仰角2°时RCS曲线Fig.6 RCS values of the sails on the water at 2°

图7 水面航态下俯仰角4°时RCS曲线Fig.7 RCS values of the sails on the water at 4°
从图5可以看出,在俯仰角0°时,指挥台围壳的RCS曲线具有典型的蝴蝶状,在方位角0°附近的角域内,模型2的RCS值略高于模型1,而在其余角域内,模型2的RCS值明显低于模型1。从图6可以看出,在俯仰角2°时,两个模型的曲线形状大致相似,模型2的RCS值在方位角0°和180°附近明显高于模型1,而在其余角域则基本略低于模型1。从图7可以看出,在俯仰角4°时,模型2的RCS值在多数角度内都大于模型1。由以上分析可以看出,在水面航态下,模型2仅在俯仰角较小时(<2°)其RCS值低于模型1;而随着俯仰角的增大,模型2的RCS值逐步呈现出全方位超过模型1。
当潜艇处于半潜航行状态时,位于俯仰角0°~4°范围内的RCS特性曲线如图8~图10所示。

图8 半潜航态下俯仰角0°时RCS曲线Fig.8 RCS values of the sails underwater at 0°
根据图8~图10可得,在半潜航态下,俯仰角0°时,模型2的RCS值全方位低于模型1;俯仰角2°和4°时,除去极少数角度外,模型2的RCS值也明显低于模型1。可以看出,潜艇处于半潜状态时,模型2的隐身性能得到了明显改善。

图9 半潜航态下俯仰角2°时RCS曲线Fig.9 RCS values of the sails underwater at 2°

图10 半潜航态下俯仰角4°时RCS曲线Fig.10 RCS values of the sails underwater at 4°
2.3 指挥台围壳雷达探测概率对比
潜艇被雷达探测到的概率与潜艇的RCS值以及潜艇与雷达的距离密切相关,而为关于俯仰角的函数,因此,本文需要探究雷达对潜艇的发现概率与雷达入射波的俯仰角以及雷达与潜艇之间距离的关系。
模拟雷达入射的数据为:n=70,Pt=1 MW,G=36 dB,λ=c/f=0.03 m,E=900,Bn=0.077 MHz,Fn=55 dB,L=20 dB。
首先,考虑距离对雷达发现概率的影响。选取重点威胁俯仰角的中间角度2°的情况,计算2个模型在水面航态和半潜航态下的发现概率,如图11所示。

图11 指挥台围壳发现概率与距离的关系Fig.11 The sails detection probabilities at different distances
观察图11中的4条曲线,从探测概率的角度来讲,当潜艇处于水面航态时,模型2的隐身性能略好于模型1;当潜艇处于半潜航态时,模型2的隐身性能明显优于模型1。当距离探测雷达在17 km以上时,处于半潜航态的模型2的探测概率已经趋近于0,已经很难被雷达探测到,而其余3种情况在距离40 km以上时发现概率才接近于0。在探测概率为10%时,处于半潜航态的模型2与雷达的距离为13 km,同为半潜航态的模型1则为30 km,模型2被雷达探测到的距离与模型1被雷达探测到的距离之比为43.3%;而相比于半潜航态,当潜艇处于水面航态时,模型2被雷达探测到的距离与模型1被雷达探测到的距离之比为94.2%。
由于潜艇处于不同方位角时RCS值差异很大,故只用一个RCS均值来计算雷达网的综合发现概率是有局限性的,只有使用不同方位角区域内的RCS均值才能真实地反映雷达网对目标综合发现概率的动态变化过程[15]。基于此原理,模仿远距离突防飞机的周向重点探测区域[16],结合潜艇指挥台围壳的RCS曲线特性,将潜艇指挥台围壳的周向划分为8个探测区域:-10°~10°为头向重点探测区域;10°~70°(-10°~-70°)为右(左)前方重点探测区域;70°~130°(-70°~-130°)为右(左)侧重点探测区域;130°~170°(-130°~-170°)为右(左)后方重点探测区域;-170°~170°为艉向重点探测区域。在计算发现概率时,用不同区域的RCS均值作为计算依据,得出相应的计算公式为:
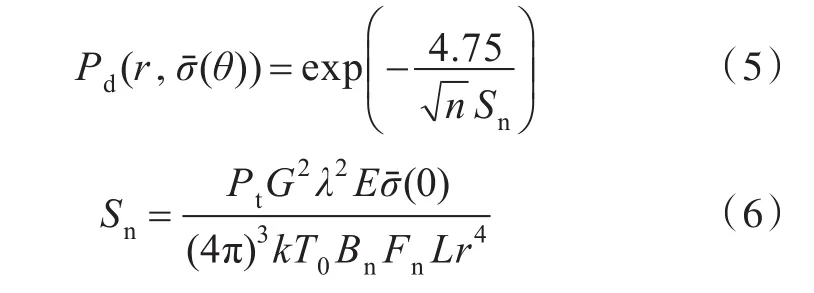
基于指挥台围壳在不同方位角范围内的RCS均值,计算其探测概率,同样选取潜艇在雷达入射波的俯仰角为2°时的情况。由于设计的指挥台围壳具有对称性,因此仅考虑右侧的重点探测区域。在距离为15 km的条件下,计算各种情况下的探测概率如图12所示。

图12 指挥台围壳在各重点探测区域的探测概率Fig.12 The sails detection probabilities at different angle territories
观察图12中的各条曲线,可以看出对指挥台围壳威胁最大的探测方位角范围为70°~130°。潜艇在水面航态时,模型2在方位角70°~170°的探测概率与模型1几乎相同,接近100%;在10°~70°探测方位角内,模型2的探测概率低于模型1;但在头部0°~10°和艉部170°~180°探测方位角内,其探测概率大于模型1,尤其是在头部,模型2的探测概率比模型1高约57%。潜艇在半潜航态时,模型2的探测概率全方位下降,在10°~180°探测方位角内均比模型1低20%左右,在头部其探测概率比模型1高约8%,但与水面航态相比,头部的探测概率明显下降,降幅约53%。
3 结 论
本文对指挥台围壳分别在水面航行状态和半潜航行状态下进行了隐身特性的数值模拟。基于高频法计算了指挥台围壳在2种航行状态下的RCS特性,并在此基础上进行了雷达发现概率计算,分析指挥台围壳的探测概率随距离变化的关系,又结合指挥台围壳外形的特点,对指挥台围壳划分雷达重点探测角后,分析各重点探测角域的探测概率。
通过数值模拟计算,得到以下结论:
1)三元流线型指挥台围壳在俯仰角很小(<2°)的情况下,能有效降低RCS,仰角增大时(>5°),其隐身特性不如直壁式围壳;
2)三元流线型指挥台围壳的低矮化设计能有效缩减RCS,在相同条件下其缩减幅度远优于直壁式围壳;
3)三元流线型指挥台围壳在水面航态时其探测距离略小于直壁式围壳,半潜航态时远小于直壁式围壳;
4)三元流线型指挥台围壳在水面航态时其侧面探测概率低于直壁式围壳,而头部和艉部探测概率则大于直壁式围壳,但在半潜航态时,能有效降低头部和艉部的探测概率;
5)在无其他隐身手段配合的情况下,将指挥台围壳设计成三元流线型其隐身特性并未明显变好,需要在此基础上配合低矮化设计其隐身性才能明显提高。
[1] 马运义,许建.现代潜艇设计原理与技术[M].哈尔滨:哈尔滨工程大学出版社,2012:81-83. MA Yunyi,XU Jian.Desing principle and technology of modern submarine[M].Harbin:Harbin Engineering University Press,2012:81-83.
[2] 胡其望.潜艇指挥台围壳模型噪声机理研究[D].哈尔滨:哈尔滨工程大学,2007. HU Qiwang.Research of noise mechanisms of submarine sail model[D].Harbin:Harbin Engineering University,2007.
[3] 吴方良,吴晓光,马运义,等.潜艇指挥台围壳对阻力和伴流场影响数值研究[J].海洋工程,2009,27(3):91-99. WU Fangliang,WU Xiaoguang,MA Yunyi,et al.The effect of submarine sail on the resistance and wake field[J].The Ocean Engineering,2009,27(3):91-99.
[4] GORSKI J J,COLEMAN R M.Use of RANS calculations in the design of a submarine sail[C]//RTO AVT Symposiun on Reduction of Military Vehicle Acquisition Time and Cost through Advanced Modelling and Virtual Simulation.Paris,France:RTO-MP,2002,33:1-12.
[5] 王志博,姚惠之,张楠.指挥台围壳对潜艇尾流影响的计算研究[J].船舶力学,2009,13(2):196-202. WANG Zhibo,YAO Huizhi,ZHANG Nan.Calculation and analysis of the effects of sail form on submarine wake[J].Journal of Ship Mechanics,2009,13(2):196-202.
[6] 刘龙举,许勇.沙丘形围壳对潜艇流场影响的数值模拟[J].四川兵工学报,2014,35(11):1-4. LIU Longju,XU Yong.Numerical study about the effect of touradon shaped submarine sail on flow field[J].Journal of Sichuan Ordnance,2014,35(11):1-4.
[7] 姬金祖,刘战合.基于面元分组的电磁遮挡算法及其优化[J].北京航空航天大学学报,2009,35(4):453-456. JI Jinzu,LIU Zhanhe.Electromagnetic occultation algorithm based on facets grouping and optimization[J]. Journal of Beijing University of Aeronautics and Astro-
nautics,2009,35(4):453-456.
[8] 苗英,万国宾,张立鹏.复杂电磁散射目标的计算机建模[J].计算机工程与设计,2006,27(1):73-75,82. MIAO Ying,WAN Guobin,ZHANG Lipeng.Geometrical modeling of complex electromagnetic scatter objects[J].Computer Engineering and Design,2006,27(1):73-75,82.
[9] 张京国,梁晓庚.基于物理光学法和面元法的目标近场RCS计算[J].探测与控制学报,2008,30(6):42-45. ZHANG Jingguo, LIANG Xiaogeng.Calculating near-field RCS of targets based on physical-optics method and panel method[J].Journal of Detection and Control,2008,30(6):42-45.
[10] 王国玉,汪连栋,王国良,等.雷达电子战系统数学仿真与评估[M].北京:国防工业出版社,2004:379-382. WANG Guoyu,WANG Liandong,WANG Guoliang,et al.Mathematical simulation and evaluation of radar electronic warfare system[M].Beijing:National Defence Industry Press,2004:379-382.
[11] 岳奎志,孙聪,刘虎,等.挂载导弹的作战飞机RCS特性数值模拟[J].系统工程与电子技术,2014,36(1):62-67. YUE Kuizhi,SUN Cong,LIU Hu,et al.Numerical simulation on the RCS of combat aircraft for mounted missile[J].Systems Engineering and Electronics,2014,36(1):62-67.
[12] 杨德庆,常少游.舰艇外形雷达隐身设计特征面法[J].中国造船,2008,49(2):113-120. YANG Deqing,CHANG Shaoyou.The characteristic cross-section method on the shape radar stealthy design of naval vessels[J].Shipbuilding of China,2008,49(2):113-120.
[13] 曹剑,张雄文.国外海军机载雷达的发展概况[J].电子科学技术评论,2005(1):8-14. CAO Jian,ZHANG Xiongwen.The development of the airborne radar on abroad[J].Review Electronics Science and Technology,2005(1):8-14.
[14] 黄培康,殷红成,许小剑.雷达目标特性[M].北京:电子工业出版社,2005:102-105. HUANG Peikang,YIN Hongcheng,XU Xiaojian.Radar target characteristics[M].Beijing:Electronics Industry Press,2005:102-105.
[15] 李莹,黄沛霖,武哲.基于不同角域RCS均值的雷达探测模型[J].北京航空航天大学学报,2008,34(6):627-629. LI Ying,HUANG Peilin,WU Zhe.Model of radar network detection based on average RCS value of different angle territory[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(6):627-629.
[16] 张考,马东立.军用飞机生存力与隐身设计[M].北京:国防工业出版社,2002:196-199. ZHANG Kao,MA Dongli.Military aircraft survivability and stealth design[M].Beijing:National Defence Industry Press,2002:196-199.
[17] 陈世春,黄沛霖,姬金祖.从探测概率的角度评价飞机的隐身性能[J].航空学报,2015,36(4):1150-1161. CHEN Shichun,HUANG Peilin,JI Jinzu.Evaluating aircraft's stealth performance from the perspective of detection probability[J].Acta Aeronautica et Astronautica Sinica,2015,36(4):1150-1161.
Numerical simulation for the stealth performance of submarine sails
XUE Fengli,HUANG Peilin,LUO Menghao,JI Jinzu
School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China
This paper studies the stealth properties of sails on the water and underwater.Based on the high-frequency method,it compares the Radar Cross Section(RCS)features of the conventional straight wall sail and the advanced 3D sail.Using CATIA and MATLAB,the numerical simulation of the RCS characteristics of sails and the calculation of radar detection probability are conducted,and the influence of different distances and angle territories on radar detection probability is discussed.The results show that the stealth performance of the advanced low-3D sail is considerably superior to that of the conventional straight wall sail.
sail;Radar Cross Section(RCS);stealth;high-frequency method;detection probability
U663.1
A
10.3969/j.issn.1673-3185.2016.06.003
2016-03-15
时间:2016-11-18 15:19
国家部委基金资助项目
薛丰利,男,1991年生,硕士生。研究方向:飞行器隐身技术,有源对消。E-mail:shadowalker@buaa.edu.cn黄沛霖,男,1975年生,博士,副教授。研究方向:飞行器总体设计,飞行器隐身技术。E-mail:peilin_h@buaa.edu.cn姬金祖(通信作者),男,1982年生,博士,讲师。研究方向:飞行器隐身技术,计算电磁学。E-mail:jijinzu@buaa.edu.cn
http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.006.html 期刊网址:www.ship-research.com
薛丰利,黄沛霖,罗蒙浩,等.指挥台围壳雷达隐身性数值模拟[J].中国舰船研究,2016,11(6):15-21. XUE Fengli,HUANG Peilin,LUO Menghao,et al.Numerical simulation for the stealth performance of submarine sails[J].Chinese Journal of Ship Research,2016,11(6):15-21.
