基于粒子群算法的螺旋桨侧斜分布优化

黄斌，熊鹰，王波

1海军工程大学，舰船工程系，湖北武汉430033

2上海船舶工艺研究所，上海200032

基于粒子群算法的螺旋桨侧斜分布优化

黄斌1，熊鹰1，王波2

1海军工程大学，舰船工程系，湖北武汉430033

2上海船舶工艺研究所，上海200032

为了降低螺旋桨激振力，减小螺旋桨对船体的诱导振动，采用粒子群优化算法，结合螺旋桨非定常面元法预报程序，对螺旋桨的侧斜分布进行优化设计。给出侧斜分布的数学表达形式以及粒子群优化算法的数学模型，并以Seiun-Maru HSP螺旋桨为母型桨进行优化设计，得到3种优化方案。其中，最优方案在不损失螺旋桨推力和扭矩的情况下，轴向一倍叶频、二倍叶频推力系数和扭矩系数明显降低，达到了优化目的，即通过改变螺旋桨侧斜分布形式，能够有效改善非均匀流场中螺旋桨的性能，验证了粒子群优化算法用于螺旋桨侧斜分布优化的可行性，可以实现工程化应用。

侧斜螺旋桨；面元法；粒子群优化算法；优化设计

0 引 言

船舶螺旋桨在船后非均匀的三向流场［1-2］中旋转一周，桨叶各半径剖面的来流攻角因各角度伴流的不同而随时改变，从而导致桨叶上承受周期性变化的螺旋桨激振力。目前，通常采用侧斜

螺旋桨来减小螺旋桨对船体的诱导振动，合理的侧斜分布形式使得螺旋桨各半径处叶剖面依次进入高伴流区［3-5］，各桨叶沿周向分布的排水体积分布更均匀，从而有效降低螺旋桨运转于非均匀流场中所产生的激振力［6］，降低船艉振动及辐射噪声。

以往对于螺旋桨侧斜分布的选择往往是根据经验公式或者参考母型，存在很大的局限性。在工程应用中，侧斜分布的选择还必须考虑到船后伴流的各阶谐调分量［7-8］，不同的伴流场需配合适当的侧斜分布形式，如果配合不当，会产生相反的效果。在螺旋桨初步设计阶段，通过对船后伴流场进行谐频分析，初步选择螺旋桨侧斜分布形式，最后再根据设计经验，通过多次人工调整来确定最终的侧斜分布形式。这种人工试探的设计方式十分繁琐，而且需要设计者拥有丰富的经验，同时使用该方法并不能确定最终的侧斜分布形式能在该非均匀流场中达到最佳的减振效果。

本文将利用粒子群优化（Particle Swarm Optimization，PSO）算法，结合螺旋桨非定常水动力性能面元法预报程序，在给定的非均匀伴流场中，以降低非定常轴承力脉动幅值为优化目标对螺旋桨的侧斜分布进行优化设计，并与母型桨的水动力性能进行对比。

1 粒子群优化算法

粒子群优化算法是通过个体间的协作与竞争，在复杂空间中搜索最优解［9］。PSO算法在可行解空间中随机初始化一群粒子，通过目标函数为每个粒子确定一个适应值（Fitness value）。每个粒子在解空间中运动，并根据一个速度确定其方向和距离。通常粒子将追随当前的最优粒子而动，经过逐代搜索，最后得到最优解。在每一次迭代过程中，粒子将跟踪2个极值，一个为粒子本身迄今找到的最优解 pbest，另一个为全种群迄今找到的最优解gbest。

PSO算法主要计算步骤［10-11］如下：

1）初始化。设定加速常数c1和c2，最大进化代数Tmax，将当前进化代数设置为t=1，在定义空间Rn中随机产生m个粒子x1，x2，···，xm，组成初始种群 X(t)，随机产生各粒子初始位移变化量ν1，ν2，···，νS，组成位移变化矩阵V(t)。

2）评价种群 X(t)，计算每个粒子在每一维空间的适应值。

3）比较粒子的适应值和自身最优值 pbest，如果当前值比 pbest更优，则令当前值为 pbest，并设 pbest位置为n维空间中的当前位置。

4）比较粒子的适应值和种群最优值 gbest，如果当前值比gbest更优，则令当前值为gbest，并设gbest为当前粒子的矩阵下标和适应值。

5）根据式（1）和式（2）更新粒子的位移方向与步长，产生新种群X(t+1)。

式中：d=1，2，···，n；i=1，2，···，m，其中m表示种群规模；t为当前进化代数；r1和r2为分布于[0，1]之间的随机数；c1和c2为加速常数。式（1）中：右边第1项为粒子先前的速度；第2项为“认知”（Cognition）部分，表示粒子自身的思考；第3项为“社会”（Social）部分，表示粒子间的信息共享与相互合作。

6）检查结束条件，若满足，则结束寻优；否则，t=t+1，转至第2）步。结束条件为寻优达到最大进化代数Tmax，或评价值小于给定精度ε。

2 侧斜分布的数学表达

1962年，法国雷诺汽车公司的工程师Bezier提出了贝塞尔曲线模型，该模型是为设计汽车零部件而提出的理论。利用贝塞尔曲线模型，可以在计算机上直接设计出各种形状。目前，其已成为CAD软件的基本模型之一，广泛应用于机械、汽车设计、字体设计等领域。

与传统的插值样条曲线不同，贝塞尔曲线是逼近拟合曲线［12］，曲线的形状比较容易控制，且直观形象。一条贝塞尔曲线的形状是由控制多边形确定的。本文采用贝塞尔曲线拟合螺旋桨的侧斜分布曲线，通过改变控制点的位置来实现拱度分布和厚度分布的重构，进而构造新的样本。通常用贝塞尔多项式作为贝塞尔曲线的基函数，一条n次贝塞尔曲线描述如下：

式中：bi（i=0，1，2，…，n）为特征多边形的顶点；Bi，n(u)（i=0，1，2，…，n）为贝塞尔多项式。

贝塞尔曲线具有良好的凸包性，拟合曲线能完全被包络在由特征多边形构成的凸包内。贝塞尔曲线的走势由特征多边形的形状决定，并且能够通过选择控制点的个数控制曲线拐点的数量。

因此，可以通过贝塞尔曲线的阶次控制贝塞尔曲线的形状，这对于拟合螺旋桨的径向参数分布非常有利，采用较低阶次的贝塞尔曲线拟合螺旋桨的径向参数分布能充分保证优化后螺旋桨的径向参数分布的合理性。

贝塞尔曲线形状只与控制点Vi的位置有关，图1所示为一条三次贝塞尔曲线和它的控制多边形。图中，p0，p1，p2，p3代表曲线的控制点。如图所示，它能够以较少的控制点位置的变化获得较大的螺旋桨设计空间，且能够满足光顺性要求。本文采用三次贝塞尔曲线拟合Seiun-Maru HSP螺旋桨的侧斜分布形式［13-15］，拟合前、后的侧斜分布曲线如图2所示。图中，r/R为相对半径，其中r为各剖面处半径，R为螺旋桨半径。

图1 三次Bezier曲线Fig.1 A three cubed Bezier curve

图2 三次贝塞尔拟合侧斜分布Fig.2 Skew distribution fitting by three times Bezier curve

3 优化模型

本文以Seiun-Maru HSP螺旋桨为母型桨，其主要参数及伴流分布参见文献［16］，采用螺旋桨非定常水动力性能面元法预报程序结合傅里叶分析方法进行计算。以轴承力的脉动幅值作为螺旋桨侧斜分布优良性的评价标准。在保证螺旋桨推力的情况下，以降低螺旋桨一倍叶频、二倍叶频轴向非定常力和力矩作为优化目标，通过调整侧斜分布来满足使目标函数最小的条件，从而达到优化螺旋桨侧斜分布的目的。图3是螺旋桨旋转一周过程中主桨叶处于0°，90°，180°和270°时0.7R处的表面压力分布与试验数值的对比图［17］。图中：纵坐标Cp为压力系数；x/c为相对弦长，其中x为叶剖面上的点沿弦长方向到导边的距离，c为叶剖面处弦长。图4所示为主桨叶在旋转一周的过程中轴向推力系数和扭矩系数的变化值及其与Hoshino计算结果［18］的对比。由图可见，本文采用的螺旋桨非定常水动力性能面元法预报程序计算精度高且稳定性好，可用于螺旋桨优化设计研究。

图3 0.7R处叶剖面非定常压力分布Fig.3 Chordwise pressure distribution of 0.7R section

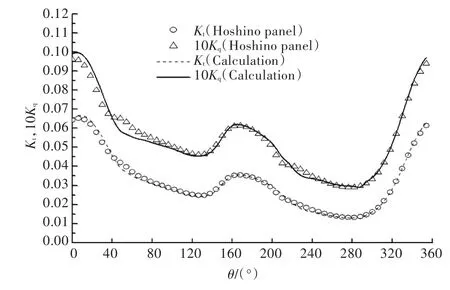
图4 主桨叶旋转一周的推力和扭矩系数Fig.4 Thrust and torque fluctuation of main blade as the propeller rotating

侧斜优化数学模型表述如下：

优化目标：Min σf

优化变量：SL≤Si≤SU

式中：i为叶频倍数；ωi为函数的权重系数；Ki为螺旋桨叶频、倍叶频轴向非定常力和力矩。在本文计算过程中，为了简化计算，只取一倍、二倍叶频的轴向力及力矩。限制条件中：σT表示优化前、后螺旋桨推力的误差；εT为可接受的推力损失限度；KT0为原始桨推力系数；KT为优化后的推力系数。通过此限制条件，在保证螺旋桨推力损失在设计者可接受范围内的前提下，优化得到目标函数最小的最优方案。优化变量Si表示螺旋桨各半径处侧斜角度，通过SL和SU来控制其上、下限，控制优化方案在合理的侧斜范围内。

本文采用贝塞尔曲线拟合螺旋桨侧斜分布曲线，优化变量Si表示的是贝塞尔曲线控制点的位置。在进行螺旋桨几何重构时，为了保证螺旋桨侧斜分布形式满足实际工程使用要求，侧斜值不能过大。因此，本研究对不同半径剖面的侧斜角给出相同的取值范围，即各半径剖面的侧斜角均在各侧斜角初始值附近20%的范围内变动。该优化变量的变化范围较大，可以保证其包含符合实际工程要求的最佳方案。

对螺旋桨非定常水动力性能产生主要影响的是前三阶非定常力和力矩，更高阶数的非定常力和力矩的量级非常小，可忽略不计。由于一阶、二阶的推力系数和扭矩系数都是影响螺旋桨性能的主要因数，其中轴承力和力矩一阶脉动幅值占主要部分，因此，本文在研究过程中同时设置一阶、二阶的轴向推力系数 KTX1，KTX2和扭矩系数KQX1，KQX2作为优化目标进行多目标优化设计，其中KTX1，KQX1的权重设置为1.0，KTX2，KQX2的权重设置为0.5。

4 优化结果分析

本文采用PSO算法对Seiun-Maru HSP螺旋桨的侧斜分布进行多目标全局优化。从最终的优化结果中，选取3个代表性的方案进行具体分析。在所选的3个方案中，方案A是综合效果最优的方案，方案B是一倍叶频脉动幅值最优的方案，方案C是二倍叶频脉动幅值最优的方案。优化方案的控制点如表1所示，优化前、后的侧斜分布形式对比如图5所示。

表1 控制点的坐标Tab.1 Coordinate of the control points

优化结果汇总如表2所示。分析发现：一倍叶频力与力矩脉动幅值具有相同的变化趋势，即同时增加、同时减小；二倍叶频力与力矩脉动幅值也具有同增同减的变化规律。

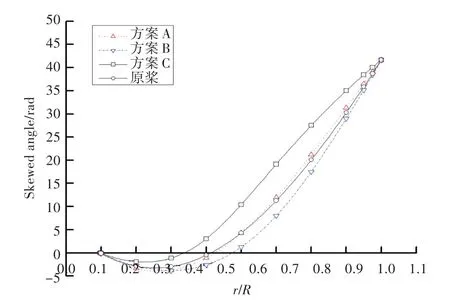
图5 优化前后侧斜分布Fig.5 Comparison of the skew distribution before and after optimization

各方案轴向推力系数及扭矩系数如图6和图7所示。从图中可以发现，轴向推力系数的平均值几乎保持没变，最高点和最低点往中间靠近，可见一阶脉动幅值有明显的减小。优化前后轴向推力系数及轴向扭矩系数的平均值分别如图8和图9所示。从图中可以发现，优化前后轴向推力系数和扭矩系数的变化非常微小。

表2 优化结果汇总Tab.2 Optimization results summary

图6 优化前后轴向推力系数Fig.6 Comparison ofKTXbefore and after optimization

图7 优化前后轴向扭矩系数Fig.7 Comparison ofKQXbefore and after optimization

优化前后各方案轴向一阶叶频推力系数和扭矩系数的对比如图10和图11所示。从图中可以看出，方案A和方案B的轴向一倍叶频推力系数和扭矩系数较母型桨明显降低，方案C的轴向一倍叶频推力系数和扭矩系数大大增加。优化前后各方案轴向二阶叶频推力系数和扭矩系数的对比如图12和图13所示。从图中可以看出，方案A的轴向二倍叶频推力系数和扭矩系数均较母型桨有明显降低。方案B也有所降低，但是降低幅度较小。方案C的轴向二倍叶频推力系数和扭矩系数较母型桨降低的幅度最大。

图8 优化前后轴向推力系数KTX平均值对比Fig.8 Comparison of the average ofKTXbefore and after optimization

图9 优化前后轴向扭矩系数KQX平均值对比Fig.9 Comparison of the average ofKQXbefore and after optimization

图10 优化前后轴向一倍叶频推力系数对比Fig.10 Comparison of 1stthrust coefficient before and after optimization

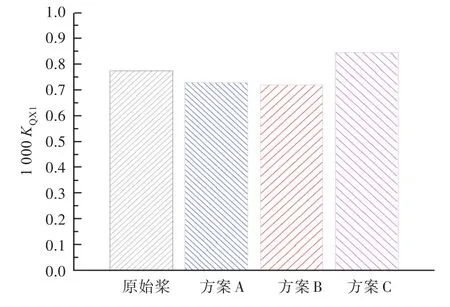
图11 优化前后轴向一倍叶频扭矩系数对比Fig.11 The comparison of 1sttorque coefficient before and after optimization

图12 优化前后轴向二倍叶频推力系数对比Fig.12 The comparison of 2ndthrust coefficient before and after optimization

图13 优化前后轴向二倍叶频扭矩系数对比Fig.13 The comparison of 2ndtorque coefficient before and after optimization

5 结 语

本文采用PSO算法，结合螺旋桨非定常水动力性能的面元法预报方法和傅里叶谐频分析方法进行螺旋桨侧斜分布多目标优化设计。优化结果表明，在不损失螺旋桨推力的情况下，优化得到的螺旋桨的一倍叶频、二倍叶频轴向非定常力和力矩明显降低。通过分析可知，在优化得到的可行性方案中，存在一倍叶频轴向非定常力和力矩减小，但二倍叶频轴向非定常力和力矩增大的情况。在利用粒子群算法进行侧斜分布优化设计的时候，需要全面考虑螺旋桨的运转工况，设置合理的权重系数以及控制点坐标。本文提供了一种新的螺旋桨侧斜分布优化的技术途径，并验证了该方法的可行性，实现了螺旋桨侧斜分布优化设计的工程化。

［1］ 王超.螺旋桨水动力性能、空泡及噪声性能的数值预报研究［D］.哈尔滨：哈尔滨工程大学，2010. WANG Chao.The research on performance of propeller's hydrodynamics，cavitation and noise［D］.Har-

bin：Harbin Engineering University，2010.

［2］ 叶永兴，杨昌培，刘绍宗.大型集装箱船上大侧斜螺旋桨模型脉动压力的比较试验研究［J］.水动力学研究与进展，1996，11（5）：535-540. YE Yongxing，YANG Changpei，LIU Shaozong.Comparative experimental study on fluctuating pressure induced by highly-skewed propeller models for a container［J］.Journal of Hydrodynamics，1996，11（5）：535-540.

［3］ YAMASAKI S，ITO M，YANAGIDA M.The effect of skew angle on the propeller induced pressure fluctuations［J］.The Japan Society of Naval Architects and Ocean Engineers，1985，70：1-13.

［4］ 叶金铭.推进器水动力性能及空泡预报的数值方法和模型试验研究［D］.武汉：海军工程大学，2008. YE Jinming.Numerical and experimental studies on hydrodynamic performance and cavitation prediction of propulsions［D］.Wuhan：Naval University of Engineering，2008.

［5］ 董世汤，王国强，唐登海，等.船舶推进器水动力学［M］.北京：国防工业出版社，2009. DONG Shitang，WANG Guoqiang，TANG Denghai，et al.Hydrodynamic of ship propulsors［M］.Beijing：National Defense Industry Press，2009.

［6］ 何友声，王国强.螺旋桨激振力［M］.上海：上海交通大学出版社，1987. HE Yousheng，WANG Guoqiang.Propeller exciting force［M］.Shanghai：Shanghai Jiao Tong University Press，1987.

［7］ HAYATI A N，HASHEMI S M，SHAMS M.A study on the effect of the rake angle on the performance of marine propellers［J］.Proceedings of the Institution of Mechanical Engineers：Part C：Journal of Mechanical Engineering Science，2012，226（4）：940-955.

［8］ 叶金铭，熊鹰，贲友稳.螺旋桨轴承力预报方法分析［J］.船舶工程，2003，25（3）：16-18. YE Jinming，XIONG Ying，BEN Youwen.Analysis of prediction method of forces exerted on propeller bearing［J］.Ship Engineering，2003，25（3）：16-18.

［9］ 徐鹤鸣.多目标粒子群优化算法的研究［D］.上海：上海交通大学，2013. XU Heming.Research on multiobjective particle swarm optimization algorithms［D］.Shanghai：Shanghai Jiao Tong University，2013.

［10］ 李宁.粒子群优化算法的理论分析与应用研究［D］.武汉：华中科技大学，2006. LI Ning.Analysis and application of particle swarm optimization［D］.Wuhan：Huazhong University of Science and Technology，2006.

［11］ 张丽平.粒子群优化算法的理论及实践［D］.杭州：浙江大学，2005. ZHANG Liping.The theorem and practice upon the particle swarm optimization algorithm［D］.Hangzhou：Zhejiang University，2005.

［12］ 朱心雄.自由曲线曲面造型技术［M］.北京：科学出版社，2000. ZHU Xinxiong.Free curve and surface modeling technology［M］.Beijing：Science Press，2000.

［13］ 蔡昊鹏，马骋，陈科，等.确定螺旋桨侧斜分布的一种数值优化方法［J］.船舶力学，2014，18（7）：771-777. CAI Haopeng，MA Cheng，CHEN Ke，et al.A numerical optimization method to determine propeller skew distribution［J］.Journal of Ship Mechanics，2014，18（7）：771-777.

［14］ 曾志波.螺旋桨叶剖面优化设计比较研究［J］.船舶力学，2011，15（12）：1344-1352. ZENG Zhibo.A comparative investigation on optimization of propeller blade section design［J］.Journal of Ship Mechanics，2011，15（12）：1344-1352.

［15］ SEARLE S，VEITCH B，BOSE N.Experimental investigation of a highly skewed propeller in ice［J］. Journal of Offshore Mechanics and Arctic Engineering，2001，123（4）：191-197.

［16］ CARLTON J S.Marine propellers and propulsion［M］.3rd ed.Oxford：Butterworth-Heinemann Ltd，2012.

［17］ 熊鹰.非均匀流中螺旋桨空泡及脉动压力的数值和试验研究［D］.武汉：武汉理工大学，2002. XIONG Ying.Numerical and experimental research on propeller-induced pressure fluctuations and cavitation in non-uniform flow［D］.Wuhan：Wuhan University of Technology，2002.

［18］ 王国强，董世汤.船舶螺旋桨理论与应用［M］.哈尔滨：哈尔滨工程大学出版社，2007. WANG Guoqiang，DONG Shitang.The theory and application of propellers［M］.Harbin：Harbin Engineering University Press，2007.

Application of particle swarm optimization theory in skew distribution of propeller

HUANG Bin1，XIONG Ying1，WANG Bo2

1 Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

2 Shanghai Shipbuilding Technology Research Institute，Shanghai 200032，China

In order to reduce the excitation force of the propeller on a ship's hull surface,a hybrid method of the Particle Swarm Optimization(PSO)algorithm of the intelligent optimized field and panel method is adopted to optimize the propeller's skew distribution.The mathematical model and main process of the PSO algorithm in the optimization design of the skew distribution is given,and a Seiun-Maru HSP propeller is taken as the prototype.Three different skew distributions are obtained through calculations.The results show that the axial coefficients of thrust and torque for the optimal scheme are reduced significantly at Blade Passing Frequency(BPF)and 2 BPF,while the thrust and torque of the propeller show no such reduction.In brief,optimizing the skew distribution of the blades effectively improves the propeller's performance in unsteady fields,and the PSO algorithm is proven to optimize skew distribution for propeller engineering.

skewed propeller；panel method；particle swarm optimization；optimization design

U664.33

A

10.3969/j.issn.1673-3185.2016.06.013

2016-05-18

时间：2016-11-18 15:19

国家自然科学基金资助项目（51479207）

黄斌，男，1991年生，硕士生。研究方向：舰船流体动力性能。E-mail：284663679@qq.com熊鹰（通信作者），男，1958年生，博士，教授。研究方向：舰船流体动力性能。E-mail：xiongying0920@163.com

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.026.html 期刊网址：www.ship-research.com

黄斌，熊鹰，王波.基于粒子群算法的螺旋桨侧斜分布优化［J］.中国舰船研究，2016，11（6）：83-89. HUANG Bin，XIONG Ying，WANG Bo.Application of particle swarm optimization theory in skew distribution of propelle［rJ］.Chinese Journal of Ship Research，2016，11（6）：83-89.