基于神经网络的火箭发动机结构动力学优化

袁军社，杨全洁，李 锋，陈守芳

（西安航天动力研究所,陕西西安710100）

基于神经网络的火箭发动机结构动力学优化

袁军社，杨全洁，李 锋，陈守芳

（西安航天动力研究所,陕西西安710100）

针对大推力液体火箭发动机研制中面临的低频结构动力学频率优化问题，采用有限元方法及试验模态方法建立了可信的发动机低频动力学模型，对结构的低频动力学特性进行灵敏度分析，提取对发动机低阶固有频率比较敏感的设计变量。以这些设计变量作为神经网络的输出，待优化的结构固有频率作为输入，通过改进的神经网络建立了映射关系，最后优化得到能使固有频率达到目标值的设计变量值。通过有限元验证，优化结果满足要求。

火箭发动机；结构动力学优化；BP神经网络

0　引言

图1　火箭发动机有限元模型Fig.1　FEM model of LRE

1　基本原理

大型液体火箭发动机非常复杂，结构是由种类繁多、特点各异的各种结构元件以焊接、铰接、螺接等连接方式构成，结构紧凑、非对称程度高[1]。所以影响其动力学特性的因素既多且复杂，使液体火箭发动机的动力学优化问题成为典型的大型复杂系统非线性动力学优化问题。

以y代表结构的优化目标（动特性参数如固有频率、振型、响应等），x代表设计参数，结构动态特性与设计参数之间一般存在函数关系

其反函数表示为

对结构模型而言，目标值y是已知的，如果可以获得准确的函数关系f-1，则结构动力学优化的“逆问题”就归结为求解设计参数目标值x的“正问题”。

传统优化方法是在有限元技术的基础上沿着准则法和数学规划法两个方向发展的[2]。这种方法对于布局简单、函数关系不复杂的结构优化设计取得了不错的效果。然而，随着大型化和复杂化的方向发展，迫切需要寻求一种可以加快优化速度、提高优化精度的方法，以解决复杂结构——液体火箭发动机的结构动力学优化问题。

2　优化设计过程

2.1优化流程

如前所述，优化已经简化为求解动力学“反问题”，物理量（如频率、振型等）与模型特征量（刚度、质量等）之间的映射关系由有限元模型表达。大多数此类问题的求解过程十分复杂，有的甚至不能得到问题的解。然而神经网络却很好地扮演物理量与模型特征量之间“数学模型”这一角色，它以物理量为因变量作为网络输入，特征量为自变量作为输出，将“反问题”归结“正问题”求解，从而避免了以上问题[3]。本文将采用基于神经网络的结构动力学优化方法，其核心就在于以神经网络映射输入和输出之间的函数关系f-1，然后根据动力学特性参数的目标值xopt优化出设计参数的目标值 。图2所示即为基于神经网络的模型修正方法流程图。

图2　基于神经网络的结构优化流程图Fig.2　Flow chart for structure optimization based on NN

2.2神经网络

由图6可得，传统Fenton反应动力学拟合曲线方程为：lnCODCr,t=0.0470t+6.9171，R2=0.9097。

神经网络从第一个数学MP模型发展至今，已经产生过几十种模型，当前研究者们已经研究出多种形式的神经网络模型，而理论最为成熟、应用最为广泛的当属基于误差反传（Error Back Propagation,BP）算法的多层前馈网络（Multipe-Layer Feedforward Network），经证明可以以任意精度逼近任意的连续函数，已经广泛应用于非线性建模、函数逼近等[4]。

标准BP算法的理论应用于各个行业领域并解决了实际问题，然而标准BP算法在应用中暴露出不少内在的缺陷：易形成局部最小而得不到全局最优；训练次数多使得学习率低，收敛速度慢；隐层节点的选取缺乏理论指导。因此，对BP算法进行了改进[5]：

2.2.1增加动量项

为了提高收敛速度，减少震荡，可以在权值调整公式中增加一动量项，含有动量项的权值调整向量表达式为

式中：α为动量系数；W(t)为节点t的权值；η为学习率；δ为梯度；X为节点输出值。

增加动量项即从前一次权值调整量中取出一部分迭加到本次权值调整量中。α称为动量系数，一般有α∈(0,1)。动量项反映了以前积累的调整经验，对于t时刻的调整起滤波作用（如图3和图4）。当误差曲面出现骤然起伏时，可减小震荡趋势，提高训练速度。

图3　α=0.9时的滤波示意图Fig.3　Schematic diagram of filtering as α=0.9

图4　α=0.98时的滤波示意图Fig.4　Schematic diagram of filtering as α=0.98

2.2.2自适应调节学习率

学习率η也称为步长，在标准BP算法中定为常数，然而在实际应用中，很难确定一个从始至终都合适的最佳学习率。在平坦区域内η太小会使训练次数增加，因而希望增大η值；在误差变化剧烈的区域，η太大会使训练出现震荡，使迭代次数增加。为加快收敛过程，一个思路就是自适应改变学习率，使其该大时增大，该小时减小。

可通过如下方法来调整学习率：设一初始学习率η0，若经过批处理权值调整后使总误差E总增大，则本次调整无效；若经过批处理权值调整后使总误差E总减小，则本次调整有效。

2.3网络训练及测试

神经网络通过样本数据来学习并实现网络输入和输出之间的映射关系。映射精度则由训练样本、训练算法和网络拓扑来保证。样本已经按照正交实验设计准则在设计空间中产生。标准BP算法使用的是近似最速下降法，然而使用标准BP算法求解实际问题是不可行的，因为它往往需要较长的训练时间，甚至是几周的时间来训练网络，所以人们对提高算法收敛速度研究给予了极大关注。目前，研究较为成熟，且应用广泛的算法有加入动量和学习率可变两种方法。本文将这两种算法同时应用于BP算法中，即学习率可变的动量BP算法。对BP网络拓扑，单隐层BP网络在隐含层神经元数足够多的情况下，能以任意精度逼近任意一个非线性映射，本文采用三层BP网络。

将正交实验设计产生的样本表[6]，以结构动特性参数（频率）为神经网络的输入，设计参数为输出代入神经网络进行训练。训练结束后，训练误差的收敛并不代表着网络已经训练成熟，还需要进行网络泛化性能的测试，否则就要调整参数（如学习率、动量因子等）重新进行训练，直至满足测试精度。当训练进行到4 000步时（图5），误差是0.005 425 31，尽管没有达到设定的目标值10-4，但误差已经收敛，可以进行网络测试以检验其泛化能力。

图5　网络训练误差收敛过程Fig.5　Convergent process of NN training error

2.4优化结果及验证

随机产生一个由6组数据组成的测试样本，通过检验神经网络泛化能力，得到测试样本的误差分布如图6所示.

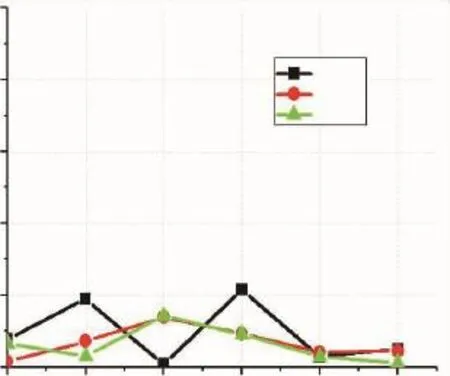
图6　神经网络测试误差Fig.6　Testing error of NN

可以看出，测试误差基本集中在10%以内，平均误差仅为3.7%，所以网络泛化能力很强，可以满足工程需要，用来替代有限元计算。考虑目前发动机结构动力学的优化目标，结合简化模型的特点，设定动力学优化的目标值为 [12 Hz 12 Hz 30 Hz]，代入已经训练成熟的神经网络进行仿真，将得到的优化结果进行测试，结果为[11.833 Hz 12.14 Hz 30.029 Hz]，与优化目标值[12 Hz 12 Hz 30 Hz]相比，各阶误差为1.39%，1.17%和0.01%，因此，优化得到的设计参数结果是可信的。

3　结论

在有限元和结构优化理论的基础上，结合已建立的结构动力学模型进行了模态分析，以对发动机固有频率敏感的部件参数为优化设计参数，采用正交实验方法设计了训练样本，通过加入动量项和调节学习率的BP神经网络映射出能达到目标的结构设计参数，并对仿真结果的正确性进行了验证，取得了良好效果。

[1]杜飞平,谭永华,陈建华.航天器子结构模态综合法研究现状及进展[J].火箭推进,2010,36(3):39-45. DU Feiping,TAN Yonghua,CHEN Jianhua.Status and progress on substructural modal synthesis techniques for space vehicles[J].Journal of rocket propulsion,2010,36 (3):39-45.

[2]钱令希.工程结构优化设计[M].北京:水利电子出版社, 1983.

[3]李锋,袁军社.BP神经网络在结构边界参数识别中的应用[J].火箭推进,2009,35(4):30-33. LI Feng,YAN Junshe.Application of BP neural network in characteristics identification of frame structure[J]. Journal of rocket propulsion,2009,35(4):30-33.

[4]费庆国,李爱群,张令弥.基于神经网络的非线性结构有限元模型修正研究[J].宇航学报,2005,26(3):267-270.

[5]韩力群.人工神经网络理论、设计及应用[M].2版.北京:化学工业出版社,2007.

[6]赵选民.实验设计方法[M].北京:科学出版社,2010.

（编辑：王建喜）

Neural network based structural dynamics optimization for liquid rocket engine

YUAN Junshe,YANG Quanjie,LI Feng,CHEN Shoufang
（Xi’an Aerospace Propulsion Institute,Xi’an 710100,China）

The finite element method and experimental modal method were adopted to build a credible low-frequency dynamics model for solving the problem of the frequency optimization in low-frequency structural dynamics,which must be faced with in development of the high thrust LRE (liquid rocket engine).The sensitivityanalysis for low-frequencydynamics characters of the structure is done to find out the design variables sensitive to inherent frequencies at low frequency of LRE.Taking these design variables as the outputs of the neural network and the structural inherent frequencies under optimization as the inputs,the mapping relationship between the inputs and outputs is established by the improved neural network,and the design variables which can make inherent frequency reach the target value is obtained by optimization.The verification result of FEM shows that the design variables can meet the system requirements.

liquid rocket engine;structural dynamics optimization;BP neural network

V434-34

A

1672-9374(2016)04-0053-05

2016-03-22；

2016-05-17

袁军社（1982—），男，硕士，研究领域为发动机强度试验