非下采样轮廓波域混合统计模型红外图像降噪方法
2016-12-10刘刚王明静周珩张喜涛
刘刚+王明静+周珩+张喜涛


摘要: 针对红外图像易受噪声污染、 成像质量差等问题, 提出一种非下采样Contourlet域变换系数混合统计建模的降噪方法。 将图像变换到非下采样Contourlet域, 对噪声系数、 信号系数分别按照高斯分布和广义拉普拉斯分布建模, 利用贝叶斯框架下的最大后验估计理论, 推导原始信号系数估计公式, 并对包含噪声的图像系数进行处理, 实现非下采样Contourlet域红外图像降噪。 实验结果表明, 该方法能够对红外成像过程中产生的高斯噪声实现有效抑制, 较完整地保持图像的边缘等细节信息, 在峰值信噪比提高与视觉效果上优于部分经典算法。
关键词: 红外图像; 降噪; 非下采样Contourlet变换; 拉普拉斯分布
中图分类号: TP391.41文献标识码: A文章编号: 1673-5048(2016)05-0066-05
Abstract: For the denoising problem of infrared image, an algorithm is proposed based on mixed statistical model of transform coefficients in nonsubsampled Contourlet domain. The image is transformed into nonsubsampled Contourlet domain, and noise coefficients and signal coefficients are modeled respectively by Gaussian distribution and generalized Laplacian distribution. By using maximum a posteriori estimation theory under Bayesian framework, a new estimation formula for the original signal coefficients is deduced, and the noise image coefficients are processed to realize the infrared image denoising of nonsubsampled Contourlet domain. The experimental results show that the proposed method can suppress the Gaussian noise effectively and keep most of the images detail information, which has higher value of peak signal noise ratio and better visual effect than some standard algorithms.
Key words: infrared image; denoising; nonsubsampled Contourlet transform; Laplacian distribution
0引言
红外图像噪声丰富, 而噪声造成图像退化、 图像特征被掩盖, 直接影响图像分割、 特征提取等后续工作的准确性, 因此, 抑制红外图像噪声、 提升图像质量是红外成像应用中图像处理和分析的前提。
小波变换具有良好的时频局域化特性和多分辨率特性[1], 在图像降噪中得到了广泛的应用[2-5]。 小波变换在表示具有点奇异性的函数时是最优基, 但是对于更高维的特征则显得力不从心。 在二维图像中, 边缘、 轮廓和纹理等具有高维奇异性的几何特征包含了大部分信息, 对此, 小波不是表示图像的最优基。
Do等人提出的Contourlet变换是一种真正的图像二维表示方法, 其将小波的优点延伸到高维空间, 能够更好地刻画高维信息的特性, 更适合处理具有超平面奇异性的信息[6-7]。 但是, Contourlet变换不具备平移不变性, 在利用其进行图像去噪时, 奇异点周围会引入伪吉布斯(Gibbs)现象。 此外, Contourlet变换存在下采样过程, 因此低频子带和高频子带均存在频谱混叠现象。 频谱混叠造成同一方向的信息会在几个不同方向子带中同时出现, 这在一定程度上削弱了其方向选择性。
Cunha等人[8-9]利用非下采样塔式分解和非下采样滤波器组构造出了非下采样Contourlet变换(Nonsubsampled Contourlet Transform, NSCT), 具有平移不变性。 NSCT继承了Contourlet变换的良好特性, 变换后系数能量更加集中, 能够更好地捕捉和跟踪图像中重要的几何特征。 同时, 由于没有采样过程, 图像的分解和重构过程中不具有频率混叠项, 这使得NSCT具有平移不变性。
在图像降噪中应用Contourlet和NSCT, 最常用的是传统的阈值方法[10-14]。 该类方法的缺点在于没有考虑到各图像尺度内系数的相关性、 相邻尺度系数之间的相关性以及边缘轮廓的关系, 图像细节信息不能很好地保留且存在振铃现象。 建立变换系数尺度内和尺度间的统计模型是在变换域还原信号系数、 抑制噪声系数的关键问题[15]。
红外成像应用中的红外探测器是系统噪声的主要来源, 是影响红外图像质量的主要因素, 其强度一般情况下远大于其他环节产生的噪声, 同时也是最难以克服的。 探测器本身的噪声是无法避免的, 按照其产生的机理可分为散粒噪声、 热噪声、 光子噪声、 产生复合噪声和1/f噪声等。 其中散粒噪声、 热噪声、 光子噪声和产生复合噪声所产生的探测器电流输出是一个随机过程, 由中心极限定理近似服从高斯分布。 1/f噪声是红外探测器低频部分的一种电流噪声, 顾名思义, 1/f噪声与频率成反比, 当高于一定频率时, 与其他噪声相比可忽略不计。 因此, 可认为影响红外图像质量的噪声服从高斯分布[16]。
航空兵器2016年第5期刘刚等: 非下采样轮廓波域混合统计模型红外图像降噪方法基于以上分析, 在NSCT域提出了一种新降噪方法。
1NSCT域混合统计图像降噪模型
1.1NSCT理论
NSCT与Contourlet变换一样, 也是采用由拉普拉斯金字塔变换与方向滤波器组所构成的双迭代滤波器组结构。 但NSCT采用的是非下采样塔式滤波器和非下采样方向滤波器组, 变换时首先由非下采样塔式滤波器将图像分解为低通(低频)部分和带通(高频)部分, 然后由非下采样方向性滤波器组将带通部分分解为若干个方向。 NSCT去掉了塔式分解和方向性滤波器组分解中信号经分析滤波后的下采样(抽取)以及综合滤波前的上采样(插值), 而改为对相应的滤波器进行采样, 再对信号进行分析滤波和综合滤波。
1.2混合统计降噪模型
NSCT域信号系数尺度间和尺度内同方向子带内相关性强, 噪声系数层间相关性较弱、 层内无相关性。 基于此, 将NSCT系数分为噪声系数和信号系数两类并分别建模, 根据贝叶斯框架下的最大后验估计理论, 推导降噪方程。
信号系数包含了图像的大部分信息及主要的边缘和纹理, 相邻尺度间的系数相关性较强, 分解系数的统计分布在原点处的峰值更尖锐, 并具有长拖尾, 可采用广义的拉普拉斯分布来建模。 噪声系数主要是噪声和微小细节的贡献, 采用具有强局部相关的零均值高斯分布来建模。
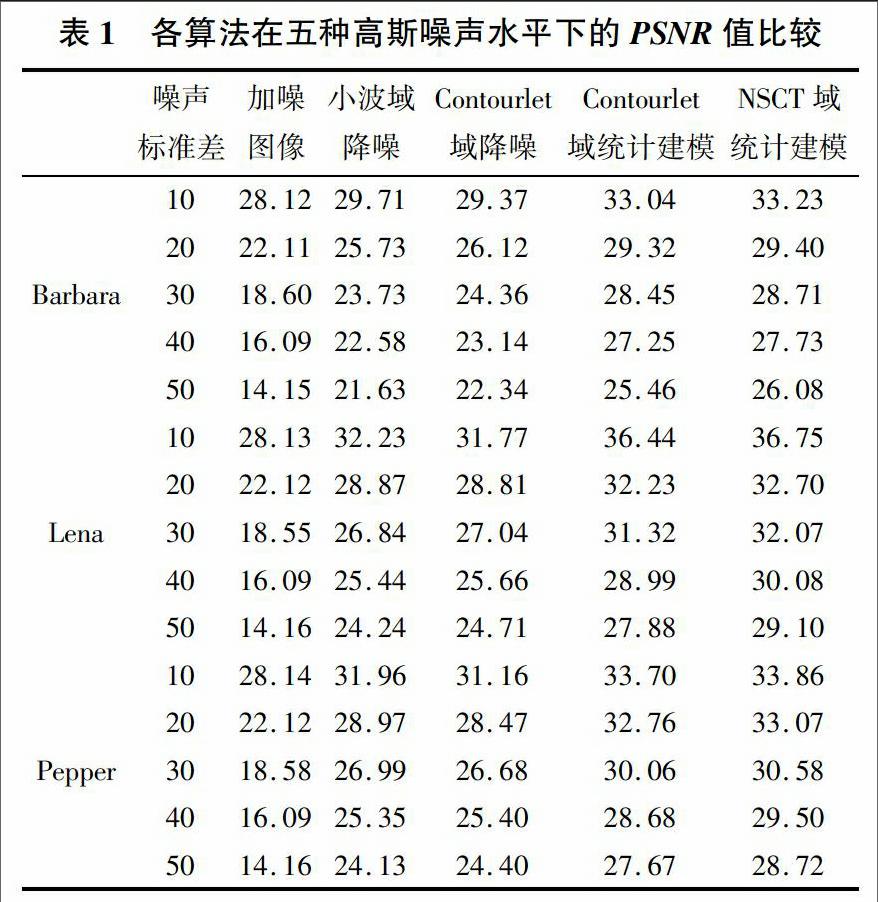
从表1、 图1~3可得出如下结论:
(1) 从表1中可知, 基于NSCT域系数混合统计模型降噪算法的PSNR最高, 能有效去除图像中的高斯白噪声, 较好地保持图像的边缘, 在噪声强度较大时, 降噪能力更加明显;
(2) 从图1、 图2和图3可知, 基于NSCT域系数混合统计模型的降噪算法既滤除了图像噪声, 又有效地保持了相关边缘细节;
(3) 基于Contourlet域混合统计模型降噪算法在视觉效果上同NSCT域方法接近, 但在PSNR上比NSCT域方法稍差;
(4) 小波软阈值法在滤除噪声的同时造成了边缘细节的模糊;
(5) Contourlet阈值降噪方法边缘细节部分保持较好, 也能有效滤除噪声, 但是出现了较为明显的栅格效应。
4结论
在NSCT域对噪声系数、 信号系数分别按照高斯分布和广义拉普拉斯分布建模, 根据贝叶斯框架下的最大后验估计理论, 推导原始信号系数的估计公式, 对包含噪声的图像系数进行处理, 实现NSCT域红外图像降噪。 NSCT具有平移不变性和更好的方向选择特性, 实验结果充分表明了本文提出的基于NSCT域系数混合统计模型的降噪方法在PSNR提高与视觉效果上优于部分经典降噪方法。
参考文献:
[1] 高静, 李朝伟, 董云峰, 等.空空导弹导引头小波降噪参数优选仿真研究[J].航空兵器, 2010(5): 48-54.
[2] 徐小军, 王友仁. 基于离散分数阶正交小波变换图像降噪新方法[J].电子学报, 2014, 42(2): 280-287.
[3] 张田, 孙延奎, 田小林.二进小波与扩散滤波结合的光学相干层析图像降噪[J].吉林大学学报(工学版), 2013, 43(S1): 340-344.
[4] 金炜, 周亚训, 符冉迪, 等.采用零树结构分类小波系数的红外图像降噪[J].光电工程, 2012, 39(5): 79-83.
[5] Donoho D L. DeNoising by SoftThresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627.
[6] Po D DY, Do M N. Directional Multiscale Modeling of Images Using the Contourlet Transform[J].IEEE Transactions on Image Processing, 2006, 15(6): 1610-1620.
[7] Do M N, Vetterli M. The Contourlet Transform: An Efficient Directional Multiresolution Image Representation[J]. IEEE Transastions on Image Processing, 2005, 14(12): 2091-2106.
[8] Cunha A L, Zhou Jianping, Do M N. The Nonsubsampled Contourlet Transform: Theory, Design and Applications[J].IEEE Transactions on Image Processing, 2006, 15(10): 3089-3101.
[9] Zhou Jianping, Cunha A L, Do M N. Nonsubsampled Contourlet Transform: Construction and Application in Enhancement[C]∥Proceedings of the IEEE International Conference on Image Processing, 2005: 469-472.
[10] 戴维, 于盛林, 孙栓. 基于Contourlet变换自适应阈值的图像去噪算法[J].电子学报, 2007, 35(10): 1939-1943.
[11] 刘丽萍, 崔宁海, 王琰.一种新的Contourlet变换图像降噪算法[J].沈阳理工大学学报, 2012, 31(1): 31-35.
[12] 程光权, 成礼智.基于冗余Contourlet变换的图像相关法去噪[J].中国图象图形学报, 2008, 13(9): 1678-1682.
[13] 倪超, 李奇, 夏良正.基于非下采样Contourlet扩散滤波的红外图像降噪[J].东南大学学报(自然科学版), 2010, 40(S1): 272-276.
[14] 闫晟, 刘明刚, 原建平, 等. 一种基于NSCT变换的超声图像降噪新算法[J].仪器仪表学报, 2012, 33(5): 1005-1012.
[15] 王文, 芮国胜, 王晓东, 等.图像多尺度统计模型综述[J].中国图象图形学报, 2007, 12(6): 961-968.
[16] 陈维真, 周晓东, 张春华.基于探测器噪声分析的红外图像增强算法[J].红外与激光工程, 2008, 37(S1): 44-47.
