拉裂—滑移式破坏的土坡地震稳定性拟静力分析
2016-12-10刘博孙树林刘俊王恩喜陈怿旸
刘博,孙树林,2,刘俊,王恩喜,陈怿旸
(1.河海大学地球科学与工程学院,南京 211100;2.河海大学水文水资源与水利工程科学国家重点实验室,南京 210098)
拉裂—滑移式破坏的土坡地震稳定性拟静力分析
刘博1,孙树林1,2,刘俊1,王恩喜1,陈怿旸1
(1.河海大学地球科学与工程学院,南京 211100;2.河海大学水文水资源与水利工程科学国家重点实验室,南京 210098)
拉裂—滑移式破坏是垂直卸荷裂隙发育的土质边坡失稳形式之一。根据土坡拉裂—滑移型破坏特征,建立边坡破坏概化模型,结合圆弧法和拟静力法推导出地震作用下垂直裂隙发育的土坡稳定性系数计算公式,并进行算例分析。结果表明:随着裂隙深度以及水平地震加速度(Kh)、垂直地震加速度(Kv)的增大,边坡稳定性系数逐渐减小;竖直向上的地震力有利于边坡的稳定性,而竖直向下的地震力不利于边坡的稳定性;较大的裂隙深度会减小地震力对边坡稳定性的影响,但不利于边坡的稳定;随着Kh的增大,Kv对边坡安全系数的影响逐渐减小,相应的随着Kv的增大,Kh对边坡安全系数的影响也逐渐减小。
边坡稳定性;垂直裂隙;地震;拟静力分析
0 引言
天然土质边坡顶部常发育有垂直卸荷裂隙。在降雨入渗、地震等因素作用下,裂隙发生扩展,可能导致边坡失稳。拉裂—滑移式边坡破坏模式是垂直裂隙发育的边坡中较为常见的破坏类型[1]。Terzaghi首先提出垂直裂隙发育深度存在一定的范围,其最大深度由土体的性质决定[2];有学者以极限平衡分析法为基础,对拉张裂隙发育的边坡稳定性进行了分析;王根龙[6]等根据离散元数值模拟,研究了黄土拉裂滑移-崩塌的破坏模式[3-5];叶万军等对拉裂-滑移式黄土崩塌的形成机制及其稳定性进行了研究[7],但至目前为止,对于土质边坡发生拉裂—滑移式破坏的稳定性进行理论计算的研究相对较少,且未考虑地震作用对其稳定性的影响[8-10]。
本文旨在考虑地震作用下,建立垂直卸荷裂隙发育的土质边坡破坏模型,结合圆弧法和拟静力法[11-13],推导出垂直裂隙发育的土质边坡稳定性计算公式,分析裂隙深度以及水平和竖直地震加速度系数Kh和Kv的大小对边坡稳定性的影响。
1 土坡拉裂—滑移型破坏形成过程
天然土质边坡卸荷裂隙常发育于边坡的中上部,呈张性,上宽下窄呈楔形,其深度受坡内土体特性、坡高和坡度等因素控制。在卸荷裂隙的影响下,边坡常发生拉裂—滑移式破坏,其破坏过程经历了坡顶拉裂阶段、垂直裂隙扩展阶段和边坡整体破坏阶段[14],如图1所示。
坡体最终形成上陡下缓的“L”型滑动面,该滑动面由垂直裂隙之间形成的近直线型滑动面和靠近坡脚坡体内的圆弧型滑动面组成。在确定滑动面时,要先确定圆弧形滑动面与近直线型滑动面的接触点位置(图1中C点)以及直线型滑动面的倾角(图1中β角),从而确定边坡整体滑动面。本文给予C点及β角一定的取值范围,计算出边坡安全系数最小的滑动面即为边坡的最危险滑动面。
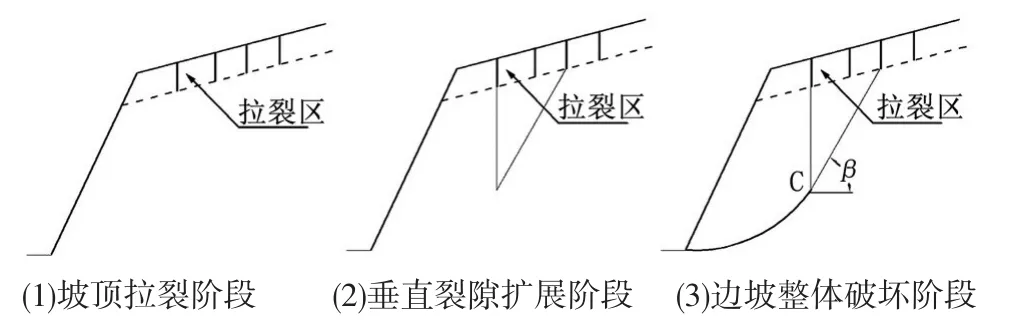
图1 裂隙发育的边坡拉裂—滑移型破坏过程Figure 1 Fissure developed slope pull-apart-sliding destruction process
2 稳定性分析公式的推导
2.1拉裂—滑移破坏边坡概化模型
如图2建立模型,该边坡模型的滑动面为复合曲面,由圆弧滑动面ABC和与圆弧面相交的直线滑动面CD组成。边坡坡顶坡比为1∶m,坡面坡比为1∶n,坡面高度为H,坡顶发育有垂直裂隙区,且垂直裂隙的高度为h0,坡脚A到坡肩G的水平距离为b。该边坡均质土的粘聚力、内摩擦角和天然重度分别为c、φ、γ。如图建立坐标系,坡脚A点位于x轴上y轴左侧,坡肩G点位于y轴上x轴上方,圆弧段圆心O点的坐标为(ε,η),C点的坐标为(μ,υ),圆弧与直线交点C点处切线与水平线的夹角为α,直线滑动面CD的倾角为β。
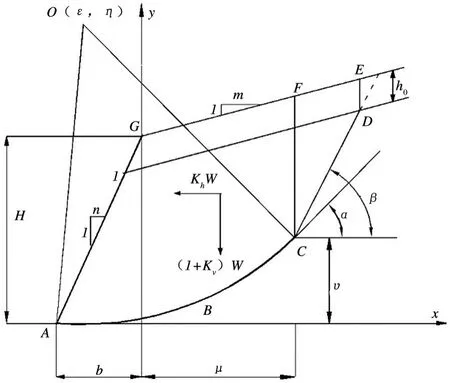
图2 边坡模型破坏模式图Figure 2 Slope model destruction mode
Kh和Kv分别为水平和竖直地震加速度系数,将地震力分为作用在边坡土体上的水平力和竖直力,其值分别为水平和竖直地震加速度系数与土体密度的乘积KhW和KvW。
在稳定性分析中,做出如下几点假定:
(1)滑动面ABC为圆弧形,C点处切线与水平线的夹角α取值为
(2)滑动面CD为直线型,其倾角β的取值为:α≤β≤90°。
(3)垂直裂隙深度h0由土体性质决定,计算公式为:
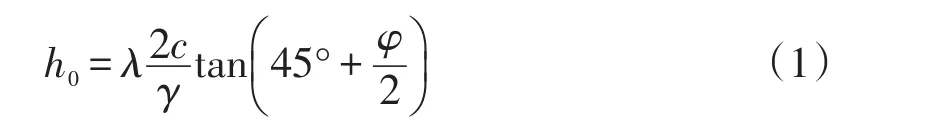
λ为修正系数,0<λ≤1,λ取值越大,裂隙深度越大。
2.2稳定性系数计算
假定圆弧破裂面ABC中C点的坐标(μ,υ)以及夹角α已知,则圆弧ABC的圆心坐标(ε,η)与半径R可求,公式如下:

圆弧ABC方程表示为:
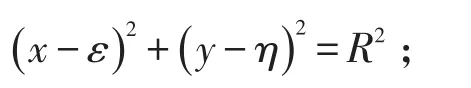
圆弧ABC上任意点的倾角αi表示为:

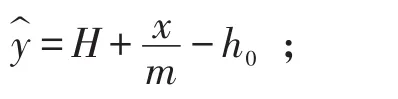
则直线CD与直线ID的交点D的横坐标为:
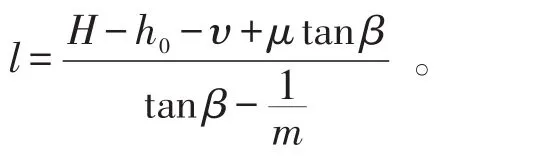
2.2.1对圆心O点滑动力矩Mr的计算
对圆心O点滑动力矩:Mr=Mr′+Mr″,Mr′为土体ABCFG自重与作用在土体ABCFG上的地震力(水平地震力和竖直地震力)的合力产生的力矩,Mr″为土体CDEF自重与作用在土体CDEF上的地震力(水平地震力和竖直地震力)的合力产生的力矩。计算公式如下:
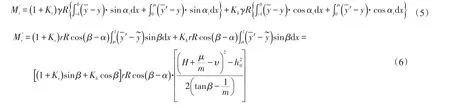
2.2.2对圆心O点的抗滑力矩MS的计算
对圆心O的抗滑力矩为:Ms=Mφ+MC,Mφ为滑动面上摩擦力产生的力矩,MC为滑动面上粘结力产生的力矩。滑动面上摩擦力产生的力矩为:为滑动面ABC上摩擦力产生的力矩,Mφ″为滑动面CD上摩擦力产生的力矩。滑动面上粘结力产生的力矩为:MC=MC′+MC″,MC′为滑动面ABC上粘结力力产生的力矩,MC″为滑动面CD上粘结力产生的力矩。计算公式如下:
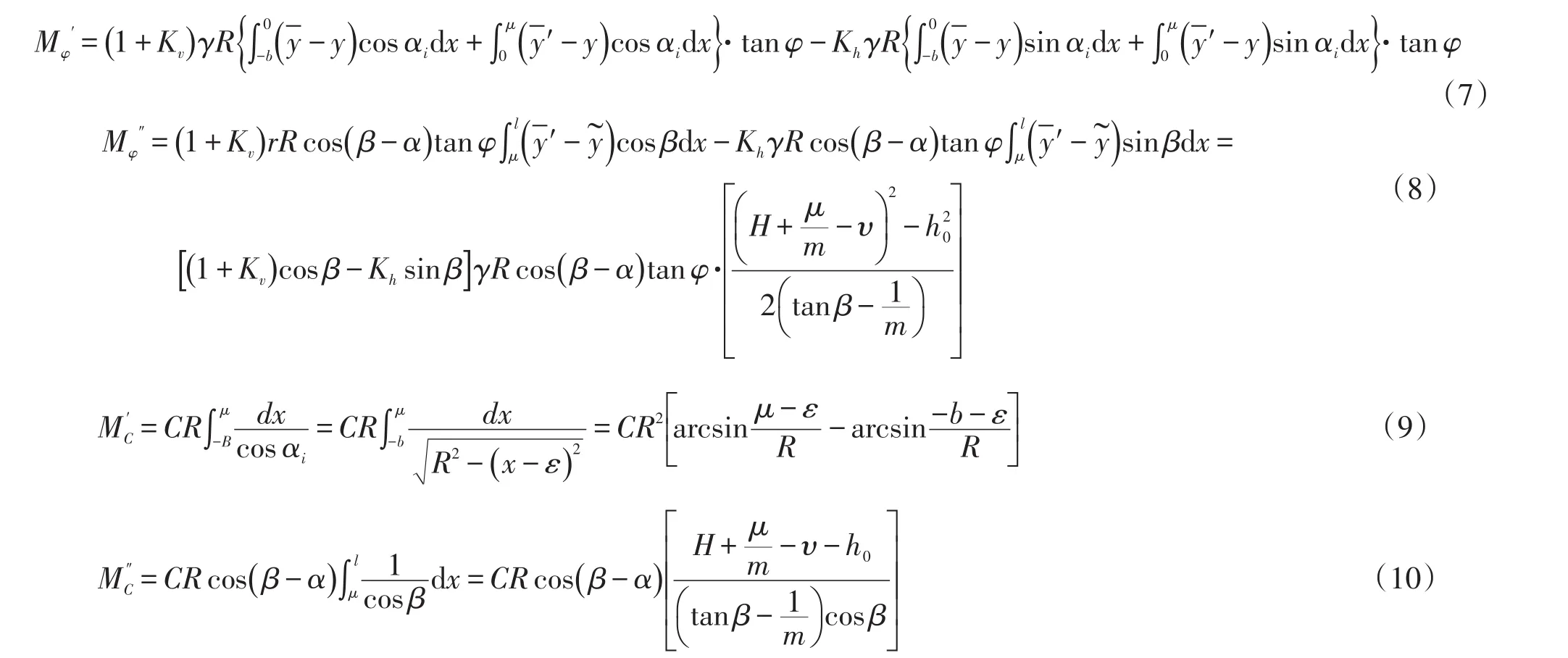
式(5)和式(7)中的各积分项计算公式如下:

(1)当α<β<90°时,边坡破坏面为由圆弧面ABC、直线型滑动面CD和裂隙面DE组成的破坏面,边坡的稳定性系数计算公式表示为:
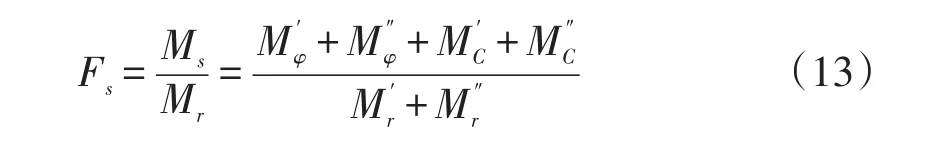
(2)当β=α时,边坡破坏面为由圆弧面ABC、与圆弧面ABC相切的直线型滑动面CD和裂隙面DE组成的破坏面,式(8)、式(10)和式(6)化为:
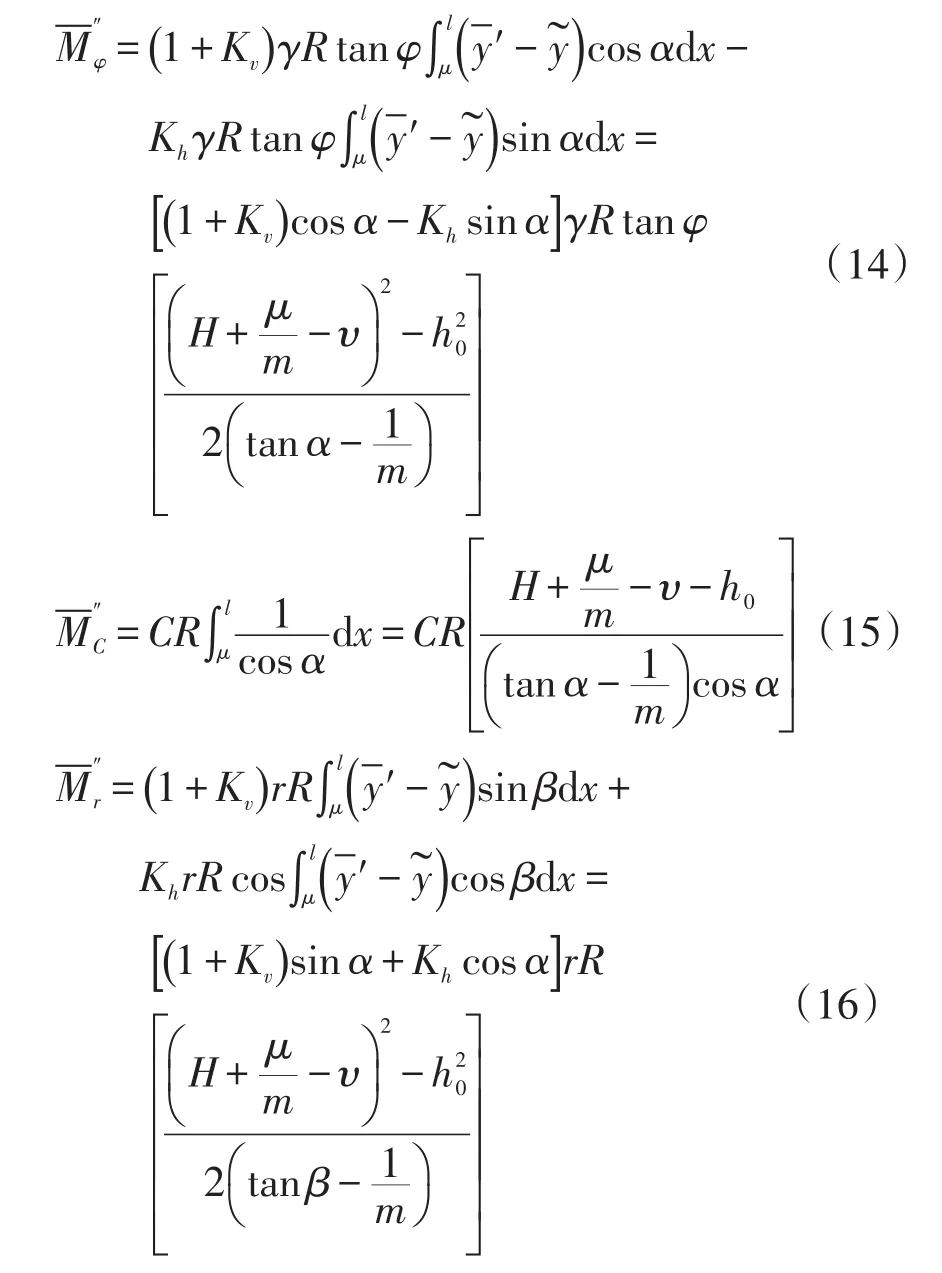
相应的边坡稳定性系数计算公式表示为:
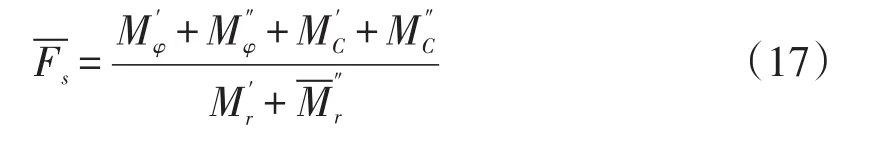
(3)当β=90°时,边坡破坏面变为由圆弧面ABC和垂直裂隙面CF组成的破坏面,相应的边坡稳定性系数计算公式表示为:

从上述公式可看出在已知水平和垂直地震加速度系数Kh、Kv,边坡均匀土体参数c、φ、γ以及边坡高度和坡度参数H、m、n的条件下,对于一组确定的参数 μ、υ、β便可算出对应的边坡稳定性系数。根据边坡的具体参数,给与μ、υ合适的取值范围。
当α<β<90°时,将μ、υ、β以一定的步长代入式(13)中进行循环运算,比较得出最小的稳定性系数即为该边坡的稳定性系数。
当β=α或β=90°时,将μ、υ以一定的步长代入式(17)或式(18)中进行循环运算,比较得出最小的稳定性系数即为该边坡的稳定性系数。
3 案例分析
3.1边坡模型
某边坡坡高H=33 m,坡脚到坡肩的水平距离b= 19 m,坡顶垂直裂隙发育,坡面坡比为1∶0.58,坡顶面水平,土质较均匀,土层参数为:c=76.5 kPa,φ= 25.3°,γ=18.5 kN/m3。裂隙深度修正值λ的取值为:0~1,水平地震加速度系数Kh的取值为:0~0.3,竖直地震加速度系数Kv的取值为:-0.2~0.2。
3.2结果分析
3.2.1与圆弧法对比分析
当Kh取值为0.1、λ取值为0.5时,分别应用圆弧法和本文方法对不同Kv值下的边坡稳定性系数进行计算,结果如图3所示。
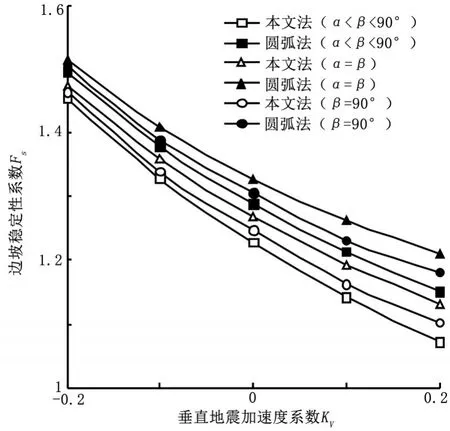
图3 不同Kv下边坡稳定性系数对比图Figure 3 Comparison chart of slope stability coefficient under different Kv
从图3中可以看出按照本文方法计算得出的边坡稳定性系数比圆弧法所得的结果偏小。随着Kv的增大,两种方法所得边坡稳定性系数逐渐减小。当α<β<90°时计算所得边坡稳定性系数相对最小,当β=90°时计算所得边坡稳定性系数相对较大,当β=α时计算所得边坡稳定性系数相对最大。
3.2.2不同裂隙深度下Kh对边坡稳定性的影响
当α<β<90°时,选取λ分别为0.1、0.3、0.5、0.7,Kh从0到0.3的边坡稳定性系数数据进行分析作图,如图4所示。并计算出Kh从0增加到0.3后的边坡安全系数的变化率,如表1所示。
从图4中可以看出,边坡稳定性系数随着Kh的增大而减小。随着Kh的增大,边坡稳定性系数的变化曲线呈现出上陡下缓的趋势,说明边坡稳定性系数减小的趋势逐渐变缓。综合图4中的四幅图可以看出随着裂隙深度的增大,边坡稳定性系数逐渐减小,当Kv=-0.2,Kh=0时,随着λ从0.1增大到0.7,边坡稳定性系数从1.69减小到1.56。
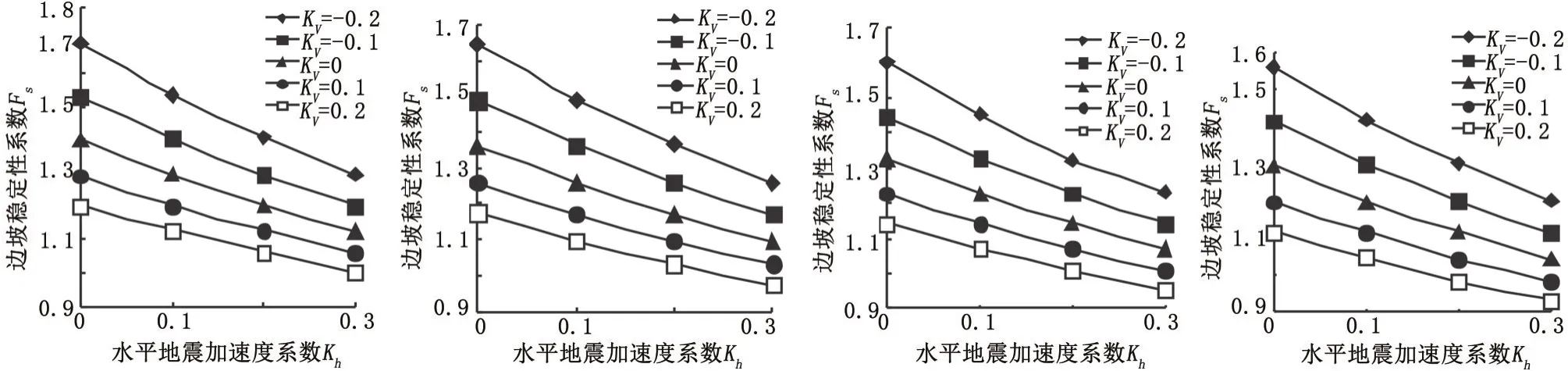
图4 不同裂隙深度下Kh对边坡稳定性系数的影响Figure 4 Impact of Khon slope stability coefficient under different fissure depths
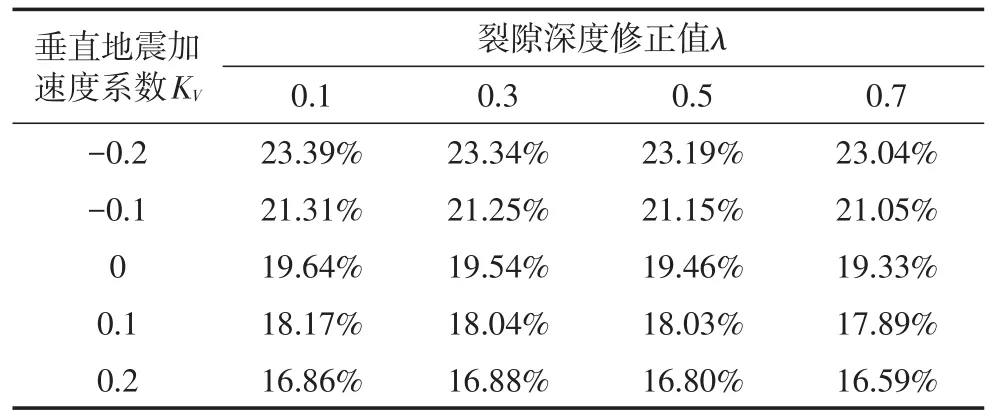
表1 Kh从0增加到0.3后边坡稳定性系数的变化率Table 1 Variance ratio of slope stability coefficient after Khincreased from 0 to 0.3
从表1中可以看出,随着Kh从0增加到0.3,边坡稳定性系数减小了16.59%~23.39%,且随着裂隙深度和Kv的增大,Kh对边坡稳定性系数的影响率逐渐变小。当Kv=-0.2时,随着λ从0.1增大到0.7,Kh对边坡稳定性系数的影响率从23.39%减小到23.04%,减小了0.35%;当λ=0.1时,随着Kv从-0.2增大到0.2,Kh对边坡稳定性系数的影响率从23.39%减小到16.86%,减小了6.53%。可见裂隙深度和Kv的变化会影响Kh对边坡稳定性系数的作用,且Kv的变化较裂隙深度的变化影响更大。虽然裂隙深度和Kv的增大会减小Kh对边坡稳定性系数的影响,但不利于边坡的稳定。
3.2.3不同裂隙深度下Kv对边坡稳定性的影响
当α<β<90°时,选取λ分别为0.1、0.3、0.5、0.7,Kv从-0.2到0.2的边坡稳定性系数数据进行分析作图,如图5所示。并计算出Kv从-0.2增加到0.2后的边坡稳定性系数的变化率,如表2所示。
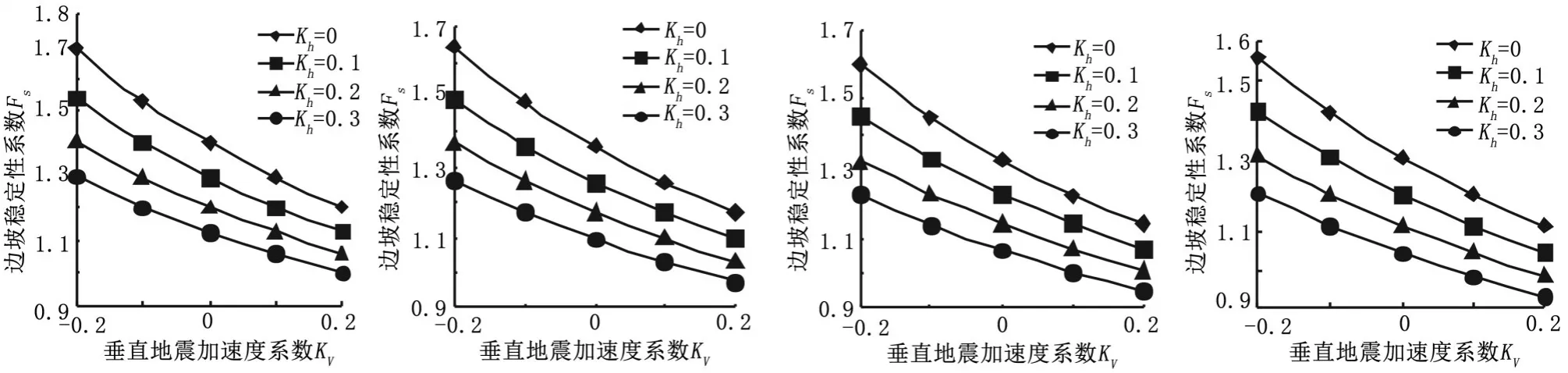
图5 不同裂隙深度下Kv对边坡稳定性系数的影响Figure 5 Impact of Kvon slope stability coefficient under different fissure depths
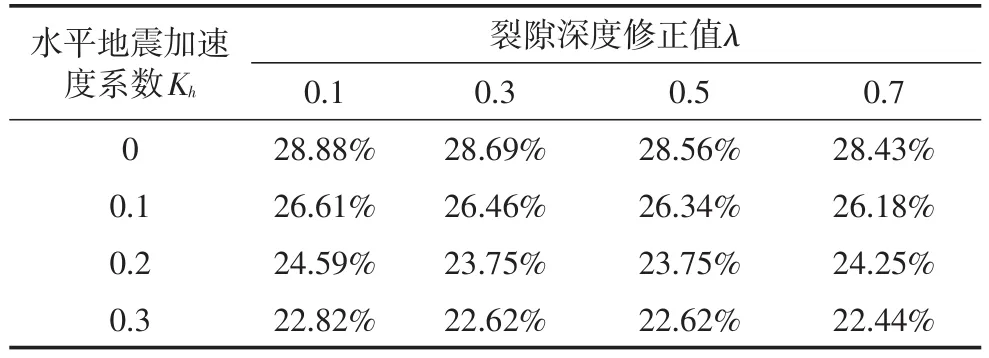
表2 Kv从-0.2增加到0.2后边坡稳定性系数的变化率Tab.2 The rate of change of the slope safety coefficient after KVincreased from-0.2 to 0.2
从图5中可以看出,边坡稳定性系数随着Kv的增大而减小。随着Kv的增大,边坡稳定性系数的变化曲线呈现出上陡下缓的趋势,说明边坡稳定性系数减小的趋势逐渐变缓。
从表2中可以看出,随着Kv从-0.2增加到0.2,边坡稳定性系数减小了22.44%~28.88%,且随着裂隙深度和Kh的增大,Kv对边坡稳定性系数的影响率逐渐变小。当Kh=0时,随着λ从0.1增大到0.7,Kh对边坡稳定性系数的影响率从28.88%减小到28.43%,减小了0.45%;当λ=0.1时,随着Kh从0增加到0.3,Kv对边坡稳定性系数的影响率从28.88%减小到22.82%,减小了6.06%。
可见裂隙深度和Kh的变化会影响Kv对边坡稳定性系数的作用,且Kh的变化较裂隙深度的变化影响更大。虽然裂隙深度和Kh的增大会减小Kv对边坡稳定性系数的影响,但不利于边坡的稳定。
4 结论
针对垂直卸荷裂隙发育的土质边坡发生拉裂—滑移式破坏的情况,建立边坡破坏模型,并结合圆弧法和拟静力法推导出地震作用下垂直裂隙发育的边坡稳定性系数计算公式。对具体的边坡案例进行计算分析得出:
(1)相对于圆弧法来说,本文方法计算出的边坡稳定性系数偏小。由于考虑边坡的破坏面为复合曲面,所以本文方法更能反映裂隙对边坡稳定性的影响。
(2)水平地震力对裂隙发育的边坡稳定性具有明显的影响,随着水平地震加速度系数的增大,边坡稳定性系数逐渐减小。较大的裂隙深度和竖直地震加速度系数会减小水平地震加速度系数对边坡稳定性系数的影响,但不利于边坡的稳定。
(3)竖直地震力对裂隙发育的边坡稳定性也具有明显的影响,竖直向上的地震力有利于边坡的稳定,而竖直向下的地震力不利于边坡的稳定。随着竖直地震加速度系数的增大,边坡稳定性系数逐渐减小。较大的裂隙深度和水平地震加速度系数会减小竖直地震加速度系数对边坡稳定性系数的影响,但不利于边坡的稳定。
(4)裂隙深度的增大会降低边坡的稳定性,且随着裂隙深度的增大,地震力对于边坡稳定性的影响逐渐减小。
[1]胡厚田.崩塌分类的初步探讨[J].铁道学报,1985,7(2):90-100.
[2]Terzaghi K.Theoretical Soil Mechanics[M].John Wiley&Sons:New York,USA,1943.
[3]Michalowski RL.Stability assessment of slopes with cracks using lim⁃it analysis[J].Canadian Geotechnical Journal,2013,50(10):1011-1021.
[4]Utili S.Investigation by limit analysis on the stability of slopes with cracks[J].Geotechnique,2013,63(2):140-154.
[5]叶万军,折学森.阶梯状黄土路堑高边坡稳定性分析方法[J].水文地质工程地质,2005,(4):75-78.
[6]王根龙,张茂省,苏天明,等.黄土崩塌破坏模式及离散元数值模拟分析[J].工程地质学报,2011,19(4):541-549.
[7]叶万军,杨更社,张慧梅,等.拉裂-滑移式黄土崩塌的形成机制及其稳定性研究[J].岩土力学,2014,12(35),3563-3568.
[8]孙强,胡秀宏,王媛媛,等.两种应变软化介质组成的边坡失稳研究[J].岩土力学,2009,30(4):976-980.
[9]张玉,徐卫亚,邹丽芳,等.降雨条件下大型滑坡体渗流稳定性分析[J].岩土力学,2013,34(3):833-841.
[10]倪卫达,唐辉明,胡新丽.黄土坡临江I号崩滑体变形及稳定性演化规律研究[J].岩土力学,2013,34(10):2961-2970.
[11]平瞳其,罗先启,郑安兴.地震作用下裂隙对岩质边坡稳定性影响分析[J].岩土力学,2015,36(2):600-606.
[12]Utili S.On the stability of fissured slopes subject to seismic action[J]. Int.J.Numer.Anal.Meth.Geomech,2016,40:785-806.
[13]邓东平,李亮.基于滑动面搜索新方法对地震作用下边坡稳定性拟静力分析[J].岩石力学与工程学报,2012,31(1):86-98.
[14]连宝琴,王新刚.节理型黄土开挖边坡塌滑破坏机理[J].煤田地质与勘探,2015,43(1):68-71.
Quasi-static Analysis of Soil Slope Earthquake Stability Pull-apart—Sliding Destruction
Liu Bo1,Sun Shulin1,2,Liu Jun1,Wang Enxi1and Chen Yiyang1
(1.School of Earth Science and Engineering,Hohai University,Nanjing,Jiangsu 211100; 2.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University,Nanjing,Jiangsu 210098)
The pull-apart—sliding destruction is one of instable forms of soil slope with developed vertical unloading fissures.Accord⁃ing to soil slope pull-apart—sliding destruction features,established slope destruction generalized model.Combined with arc method and quasi-static method deduced vertical fissure developed soil slope stability coefficient computational formula under earthquake con⁃dition and carried out numerical study.The result has shown that along with fissure depth and Kh,Kvincrease,slope stability coeffi⁃cients are gradually decreasing.Vertically upward earthquake forces are conducive to the stability of the slope,while vertically down⁃ward earthquake forces not conducive to the stability.Larger fissure depth will decrease impact of earthquake force on slope stability, but not conducive to the stability of the slope.Along with Khincreasing,impact of Kvon slope safety factor gradually decreases;corre⁃spondingly,along with Kvincreasing,impact of Khon slope safety factor also gradually decreases.
slope stability;vertical fissure;earthquake;quasi-static analysis
P642.22
A
10.3969/j.issn.1674-1803.2016.11.12
1674-1803(2016)11-0062-05
刘博(1993—),男,山西运城人,硕士研究生,主要从事地质环境与地质灾害方面的研究。
2016-05-24
责任编辑:樊小舟
