探索新公式
2016-12-09徐永华
数学小灵通·3-4年级 2016年12期
□徐永华
探索新公式
□徐永华
小朋友,我们已经知道两个数的和与一个数相乘,可以用这两个数分别同这个数相乘,再把两个积相加,结果不变,这叫做乘法分配律,用字母表示就是:(a+b)×c=a×c+b×c。能不能扩大乘法分配律的使用范围呢?例如,两个数的差与一个数相乘,用这两个数分别与这个数相乘,再把两个积相减,结果会不会改变呢?也就是能不能用字母表示为“(a-b)×c=a×c-b×c”呢?
为了回答这个问题,你不妨先计算,再比较下面两组算式:
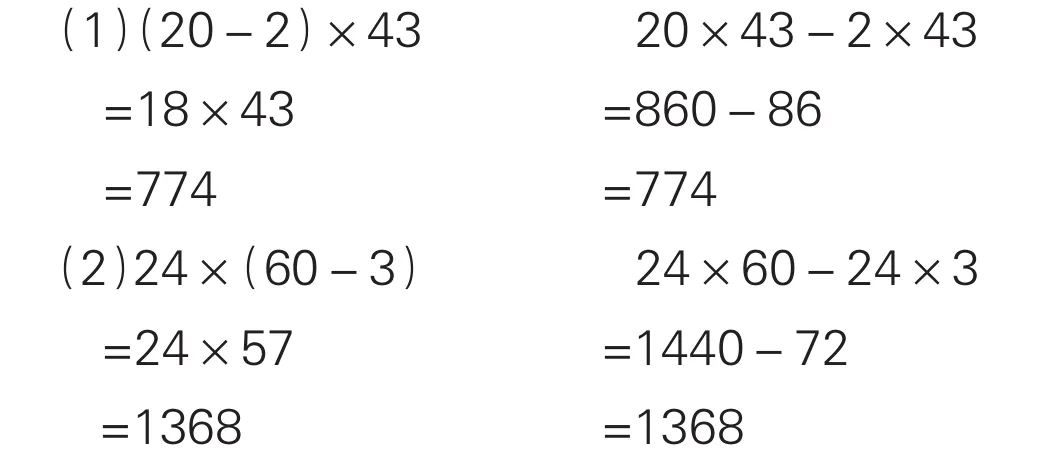
由此可见,(20-2)×43=20×43-2×43,24×(60-3)= 24×60-24×3。两个例子还不能说明问题,你不妨再多举几个类似的例子算一算,比一比。
通过计算比较,我们会发现,由乘法分配律推广出来的“(ab)×c=a×c-b×c”是正确的。利用这一结论,我们可以将一些计
算变得简便起来。
例如:36×18=36×(20-2)=36×20-36×2=720-72= 648。
再如:

小朋友,要是两个数的和除以一个不为0的数,是不是可以用这两个数分别除以这个数,再把两个商相加呢?即用字母表示为“(a+b)÷c=a÷c+b÷c(c≠0)”。两个数的差除以一个不为0的数呢?你还能想出哪些类似的问题?赶快开动脑筋探索一下吧!
(作者单位:江苏省兴化市沈伦中心小学)
