基于实地监测的常用隧道涌水量预测方法对比分析
2016-12-09张金平
张金平
(广东省交通规划设计研究院股份有限公司,广东广州 510507)
基于实地监测的常用隧道涌水量预测方法对比分析
张金平
(广东省交通规划设计研究院股份有限公司,广东广州 510507)
[目的] 揭示隧道发生涌水病害的内在原因,分析目前各种预测隧道涌水量计算方法的准确性和适用性,为相关工程及理论公式的进一步完善提供参考。[方法]采用工程地质调查测绘、钻探、物探、现场及室内实验等方法,将隧道长期涌水量记录数据与隧道涌水量计算公式所得结果进行对比。[结果]全面掌握了事故段工程地质及水文地质情况,不同公式所得涌水量预测结果相差较大。[结论]隧道发生涌水病害的内在原因主要是附近民用水塘长期蓄水;采用古得曼公式所得的预测结果与工程实测值最为接近。
隧道涌水;涌水量预测;勘察;地下水动力学法
长期以来,涌水问题一直是隧道工程中普遍存在且容易造成严重后果的工程灾害[1]。在长期水力作用下,隧道围岩与水产生物理和化学反应,使得围岩强度降低、膨胀、变形,甚至失稳破坏,给隧道长期安全服役性能带来严重挑战。针对此问题,众多工程师及科研学者进行了积极的探索,提出并拓展了多种预测隧道涌水量的理论及经验方法,主要包括:地下水动力学方法、水理统计法、水平衡法、比拟法、数值分析法、非线性理论方法等[2-7]。
其中,地下水动力学法又称解析法,是根据地下水动力学原理用数学解析的方法对给定边界条件和初值条件下的地下水运动建立解析式,从而达到预测隧道涌水量的目的。由于该方法综合考虑了隧道所处地质环境、水文地质条件、施工方式、当地气候等关键因素,在隧道涌水量计算中最为常用。主要包括:柯斯嘉科夫公式、大岛洋志公式、佐藤邦明公式、古得曼公式等[8-9]。
但总体而言,不同的公式和计算方法所得结果差别较大,迄今尚无能被一致认可的隧道涌水量预测算法。而要准确地预测隧道涌水量,选取合适的涌水量预测方法是关键。因此,笔者结合具体工程实例,在全面掌握隧道所处工程地质及水文地质情况的基础上,对目前常用的隧道涌水量预测方法进行适用性和准确性检验,积累隧道涌水量预测工程经验,为涌水量预测方法的进一步完善提供借鉴和参考。
1 隧址区地质概况
1.1 地形地貌特征 隧道穿过丘陵地貌区,地面标高158.7~236.0 m,相对高差约77.3 m。岩体节理裂隙发育,为地下水的赋存、渗流提供了物质条件。区内断裂及节理以北东走向为主,其次为北西走向。地表水体主要以距隧道右侧约127.0 m的山塘1及88.0 m的山塘2为主;山塘1水位施工前后无变化,水位0.6~1.5 m,水面标高约158.9 m,山塘2现在无水,山塘2拦水坝坝顶高程为161.0 m。山体植被茂密,并建有旅游区盘山公路。
1.2 地质构造 该项目区域地质构造主要为梅县—蕉岭山字型构造、莲花山断裂构造带及大埔—饶平北西向构造带、盆地构造。与圣人山隧道相关的主要为龙坑断裂、蛇子龙断裂、梅子坝断裂。
龙坑断裂:龙坑断裂分布于北东部西阳龙坑一带,总体走向N 80°,两端为第四系覆盖,区内延伸10.0 km,与线路在RK5+780处约45°斜交。
蛇子龙断裂:为近东西向断裂,走向约80°,区内延伸8.0 km,位于线路北侧,距RK6+000约1.0 km,属逆冲挤压型断裂,发育于震旦系老虎塘组地层中。具体特征为发育硅化构造角砾岩,角砾呈不规则棱角状,大小0.5~3.0 cm,胶结物为粉碎状岩粉,具强烈硅化。
梅子坝断裂:走向约60°,产状145°∠65°,区内延伸6.0 km,位于线路北侧,距RK6+000约1.5 km,断裂带宽10.0~20.0 m,发育于震旦系老虎塘组地层中。断层带由断层角砾及断层泥组成。
1.3 地层岩性 素填土(Qml):灰色,0~0.15 m为砼路面,0.15~0.30 m由碎石、风化土等组成。局部分布,厚度0.30~1.50 m,属强透水。
强风化变质砂岩(Z):灰白混土黄、褐红色,岩心呈碎块状,岩质软,节理裂隙发育密集,隙面锈染,变余砂质结构,层状构造,构造影响基岩破碎,岩心未见明显构造带形迹。大部分布,厚度47.70~80.60 m,中等透水。
强风化变质砂岩(Z):黄褐色,岩石风化剧烈,岩心呈半岩半土状,遇水软化,质软。零星分布,厚度为8.10 m,弱透水。
中风化变质砂岩(Z):青灰色,岩心碎块呈短柱状,节理裂隙发育,隙面锈染,岩质较硬,敲击响脆,变余砂质结构,层状构造,构造影响基岩破碎,但岩心未见明显构造带形迹。大部分布,厚度1.00~47.50 m,中等透水。
其中,对具有代表性的强风化变质砂岩层开展了常规土力学室内实验,每一测点取样不少于6个,所得土体基本物理力学参数为:含水率21.0%,密度1.9 g/cm3,土粒比重2.7,孔隙比0.7,液限28.4%,塑限18.7%,黏聚力17.0 kPa,内摩擦角33.6°,压缩系数0.27 MPa-1、压缩膜量6.2 MPa。
2 水文地质特征分析
该区地处亚热带,雨量充沛,地下水补给来源充足。丘陵范围,构造裂隙和风化裂隙发育,大部分地方植被茂盛,裂隙水广泛分布。根据梅县幅区域水文地质图(1∶20万),地下水为松散层孔隙水、基岩类裂隙水和断层破碎带水三大类水。
松散层孔隙水:广泛分布于第四系中,其中砂、砂砾为主要含水层,主要为潜水,水量贫乏。单井涌水量76.73~653.57 t/d,个别孔2 380.41 t/d,水位埋深0.21~3.85 m,水质以HCO3-Ca型为主,矿化度0.02~0.36 g/L。
基岩类裂隙水:分布于基底碎屑岩、变质岩中,如砂岩、粉砂岩、变质砂岩、千枚岩的风化裂隙和构造裂隙中,地下水的补给和排泄途径不通畅,水量较贫乏。泉常见流量0.039~0.325 L/s,地下水径流模数1.210~5.537 L/(s·km2)。水质以HCO3-Ca及HCO3-Ca.Mg型为主,矿化度0.02~0.10 g/L。
断层破碎带水:项目区内断裂构造发育,以北东走向为主,其次为北西走向。属中等—强透水层,为山塘向隧道渗水的主要通道。
3 隧道涌水量预测及分析
3.1 隧道涌水量预测常用方法 目前,预测隧道涌水量的方法多种多样,在我国常用的主要是地下水动力学方法和经验公式法,并已纳入国家行业标准及规范。
柯斯嘉科夫计算涌水量理论公式:
(1)
式中,Qs为隧道通过含水体段正常涌水量(m3/d);H为静止水位至隧道洞底距离(m);L为隧道通过含水体的长度(m);K为含水体的渗透系数(m/d);R为隧道涌水量影响宽度(m);r为隧道横断面宽度的一半(m)。
大岛洋志最大涌水量计算公式:
(2)
式中,q0为洞身通过含水体单位长度最大涌水量(m3/d);d为隧道洞身横断面等价圆直径(m);r0为洞身横断面等价圆半径(m);λ为转换系数,一般取值0.86,其他符号意义同上。
佐藤邦明非稳定流理论公式:
(3)
qs=q0-0.584εKr0
(4)
式中,q0为洞身单位长度最大涌水量(m3/d);qs为单位长度正常涌水量(m3/d);h为静止水位至洞身横断面等价圆中心的距离(m);hc为含水体有效厚度(m);λ为转换系数;ε为平均实验系数,一般取12.8,其他符号意义同上。
古得曼经验公式:
(5)
式中,Q0为隧道通过段落可能最大涌水量(m3/d),其他符号意义同上。
铁路勘测规范经验公式为
正常涌水量计算公式为
Qs=LHK(0.676-0.06K)
(6)
最大涌水量计算公式为
Q0=L(0.025 5+1.922 4HK)
(7)
3.2 隧道洞身涌水量预测 结合前期现场勘察结果并考虑到附近水塘的影响,计算图式如图1所示。
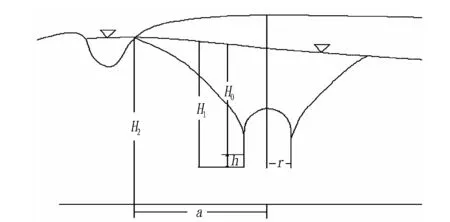
图1 隧道涌水量计算图式Fig. 1 The calculating model of tunnel water inflow
为获得隧道围岩渗透系数,在地质勘探的基础上,选取代表性的区域进行多个钻孔并开展了常水头注水实验,实验关键参数及所得成果平均值分别如下:水平、垂直方向渗透率比10,渗水段长度20 m,钻孔半径0.055 m,形状系数15.32,注入流量1 240 m3,水头高度40 m,渗透系数2.02 m/d。
利用上述公式,分别计算隧道正常涌水量与最大涌水量,结果如表1所示。
可以看出,不同的公式所得隧道涌水量相差较大,预测涌水量计算结果从小到大依次是:柯斯嘉科夫公式、佐藤邦明公式、大岛洋志公式、经验公式、古得曼公式。其中柯斯嘉科夫公式计算结果约为古得曼公式所得涌水量的一半。
3.3 隧道洞身涌水量实际检测 对该隧道涌水段分别在2011和2012年进行了隧道涌水量实地检测,得到隧道实际涌水量曲线如图2所示。
根据实地检测结果可以看出,枯水期隧道涌水量QK约为1 200 m3/d,雨期涌水量QB约2 800 m3/d,水塘蓄水后最大涌水量QX约10 540 m3/d。从而可知由于降雨增加的涌水量(QB-QK)为1 600 m3/d,由于水库蓄水增加涌水量(QX-QK)为9 340 m3/d。
梅州年降雨量1 400~1 800 mm,平均降雨量1 500 mm,降雨系数取1.2(1 800/1 500),测量精度系数取1.3,则实际总涌水量约为
Q=1.3×[QK+1.2×(QB-QK)+(QX-QK)]
=16 198
(8)
与表1所得计算结果相比较可知,常用的各预测隧道涌水量的方法均偏于保守,其中古得曼公式预测结果真实涌水量最为接近,也仅为实测值的55.69%,仍存在较大偏差。

表1 涌水量计算结果对比
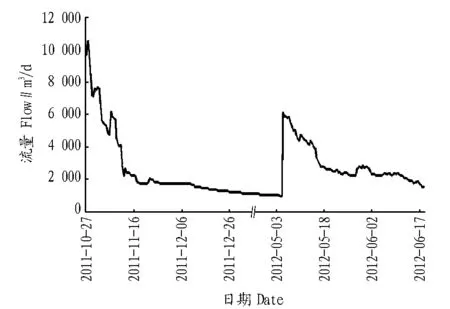
图2 涌水量曲线Fig.2 Water gushing quantity curve
4 结论
该研究结合实际工程长期涌水量监测结果,对比分析了目前常用隧道涌水量计算公式,得到以下结论:
(1)即使对于同一工况,采用不同的隧道涌水量预测方法所得到的预测结果相差也大。其中柯斯嘉科夫公式预测结果最为保守,而古得曼公式所得涌水量最大。
(2)常用的隧道涌水量预测方法与实测值相比较普遍偏
小,其中古得曼公式预测值与真实值最为接近,但也仅为实测值的55.69%。
(3)值得注意的是,对于特定的工程情况,工程地质及水文地质条件具有特殊性和复杂性,且涌水量是多种因素综合作用的结果,而目前尚无为大家所公认的计算方法,有必要总结以往工程经验进一步完善涌水量预测方法。
[1] 吕燕,邓林.大相岭隧道涌水预测数值模拟分析[J].路基工程,2010(6):90-92.
[2] 林传年,李利平,韩行瑞.复杂岩溶地区隧道涌水预测方法研究[J].岩石力学与工程学报,2008,27(7):1469-1476.
[3] 张夏临,冯涛,王晓伟.代家坳隧道涌水量计算[J].路基工程,2008(5):121-123.
[4] 职常应,李永生,罗占夫.关角隧道二郎洞断层束破碎带涌水分析[J].路基工程,2010(5):59-61.
[5] 李树忱,冯现大,李术才,等.新型固流耦合相似材料的研制及其应用[J].岩石力学与工程学报,2010,29(2):281-288.
[6] 方振华,王鹰,冯涛.贵广高速铁路坪山隧道涌水量预测及涌水防治[J].路基工程,2010(1):197-199.
[7] 潘海泽,黄涛,孙殿国.隧道涌水灾害的防治对策及工程措施量化研究[J].路基工程,2008(5):42-44.
[8] 田海涛,董益华,王延辉.隧道涌水量预测的研究[J].水利与建筑工程学报,2007,5(3):75-77.
[9] 徐国锋,杨建锋,陈侃福.台缙高速公路苍岭隧道水文地质勘察与涌水量预测[J].岩石力学与工程学报,2005(A02):5531-5542.
Comparative Analysis of Forecasting Method to Water Inflow in Tunnel Based on Field Monitoring
ZHANG Jin-ping
(Guangdong Province Communications Planning & Design Institute Co. Ltd., Guangzhou, Guangdong 510507)
[Objective] To reveal the inner causes of tunnel water gushing, analyze accuracy and applicability of the method of calculating the water inflow in the tunnel, to provide reference for further perfecting relevant project and theoretical formula. [Method] By carrying out engineering geological survey, drilling, geophysical prospecting, field and laboratory tests and combined with the long tunnel inflow water record data, the comparison and analysis were made on the method of calculating the water inflow in the tunnel. [Result] Engineering geological and hydrogeological investigation of the tunnel was made clear and it showed that the results between different formulas differ greatly. [Conclusion] The inner cause of tunnel water gushing is mainly due to long-term storage of water nearby and the prediction results from Goodman formula is more accurate than those from other formulas.
Tunnel gushing; Prediction of water inflow; Survey; Groundwater dynamics
广东省交通运输厅科技项目(201402009)。
张金平(1983- ),男,江西赣州人,高级工程师,硕士,从事岩土方向的勘察、设计及施工研究。
2016-09-07
TU 416.1
A
0517-6611(2016)31-0235-03
