一种新的组合桩轴压承载力计算

尹航, 傅睿, 罗媚, 江建林, 杨立军



一种新的组合桩轴压承载力计算

尹航, 傅睿, 罗媚, 江建林, 杨立军

(湖南文理学院土木建筑工程学院, 湖南常德, 415000)

为了解决桩径过大问题, 提出了一种新型组合桩形式, 即在普通钢筋混凝土桩内部设置沿桩身纵向连续的圆钢管。分析了新型组合桩在轴心压力作用下的受力机理, 将钢管和箍筋对混凝土的约束作用等效为有效侧向应力, 推导出了临界状态时外围混凝土的配箍率。提出了随着外围混凝土配箍率的不同, 这种桩在轴压下有2种破坏形式。分别推导出了不同破坏形式时轴心压力作用下新型组合桩承载力计算方法。采用该方法计算的组合桩轴压承载力与文献试验结果之比的平均值为1.015, 标准差为0.037, 二者吻合良好。

约束混凝土; 组合桩; 轴压承载力; 临界配箍率

桩基础通过桩把建筑上部荷载传给地基, 是一种可靠、结构形式简单的深基础形式, 在基础工程中应用广泛, 是目前研究热点之一。一些文献分别对桩的荷载传递机理[1–4]、桩的可靠性[5]、桩的相互作用因子[6]、桩的承载力计算[7–8]进行了研究。如果桩穿过并支撑在各种压缩土层, 并且主要依靠桩侧土的摩擦阻力支撑竖向荷载, 这样的桩称为摩擦桩; 如果桩顶荷载全部或主要由桩端阻力承受, 桩侧阻力相对桩端阻力而言较小, 或可忽略不计, 这样的桩称为端承桩。当采用先成孔再现场浇筑混凝土桩的施工方法时, 端承桩常常采用扩大桩底的措施增加地基承载面积, 这时如果持力层具有较大的承载力特征值, 则桩基础的承载力由端承桩桩身的轴压承载力控制。当单桩承载力设计值较高, 且采用普通钢筋混凝土桩时, 则需要较大的桩身直径。这样一方面需要较大的成孔直径, 另一方面桩身需要较多的材料。为了解决“胖桩”问题, 本文提出了一种新型的组合桩形式, 即在普通钢筋混凝土桩内部设置沿桩身纵截面连续的圆钢管。为了方便这种新型组合桩的推广应用, 本文分析了组合桩在轴心压力作用下的受力机理, 并给出了承载力计算公式。

1 临界状态下外围混凝土的配箍率

组合桩截面形式如图1所示。由于混凝土横向变形限制程度的不同, 桩内混凝土可分为核心混凝土和外围混凝土。其中, 核心混凝土是指钢管包裹的混凝土, 外围混凝土是指位于钢管和箍筋之间的混凝土。外围混凝土可以作为钢管的保护层, 保证钢管的耐久性。由于钢管是连续截面, 对混凝土的约束作用大于箍筋, 轴心压力作用下外围混凝土一般先于核心混凝土破坏。提高外围混凝土的配箍率, 加强外围混凝土的约束效应, 可以使外围混凝土和核心混凝土同时破坏, 此时的配箍率即为临界配箍率。当配箍率小于临界配箍率时, 组合桩破坏始于外围混凝土破坏, 此时核心混凝土并末达到极限状态。当配箍率不小于临界配箍率时, 组合桩破坏时核心混凝土和外围混凝土均达到极限状态。组合桩埋在地基土层中, 由于有可靠的侧向支撑, 其稳定性可以保证。组合桩轴压承载力计算时可以将其视为短柱进行计算, 不考虑桩长对组合桩轴压承载力的影响。

设组合桩和钢管的直径分别为1和2, 钢管厚度为, 螺旋箍筋、外围混凝土、钢管和核心混凝土交界面的径向应力分别为1、2和3(图2)。设螺旋箍筋抗拉强度为y1, 面积为s1, 钢管抗拉强度为y2, 则极限状态下单根螺旋箍筋承受的拉力1=y1s1, 单位长度钢管承受的环向力2=y2。

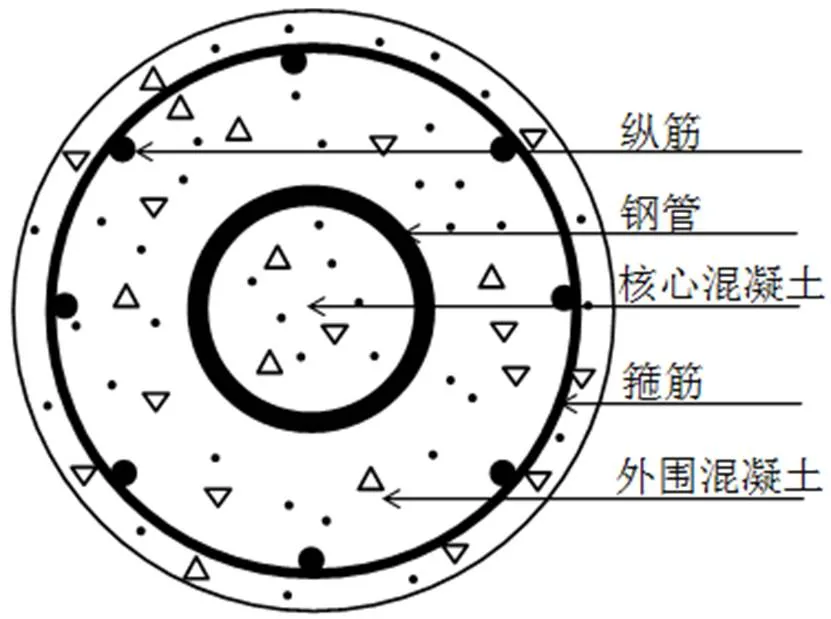
图1 组合桩截面形式

图2 组合桩计算简图

设螺旋箍筋间距为, 考虑螺旋箍筋平衡, 有

11= 21= 2y1s1。 (1)

设外围混凝土的配箍率和约束指标分别为1、1, 轴心抗压强度c1, 则有

由式(1)和式(2)可得

分别以外围混凝土和钢管为研究对象, 有静力平衡方程

利用弹性理论, 可以求得钢管外径处径向位移s和外围混凝土内径处径向位移c分别为

式(5)中:s、c分别为钢管和混凝土的弹性模量;为混凝土的泊松比。

由径向位移连续条件, 有s=c, 即

综合式(3)～(6), 并令=1/2, 可得组合桩临界状态下外围混凝土的配箍率

2 配箍率不小于临界配箍率时, 轴压承载力的计算

侧向约束力的存在提高了混凝土的轴向抗压强度, 也导致对核心混凝土和外围混凝土约束程度的不同。外围混凝土极限强度c1和核心混凝土极限强度c2分别为

式中:为侧压力系数, 一般取= 4;c2为核心混凝土轴心抗压强度。

设1、2和3分别为钢管单元的轴向应力、环向应力和径向应力。径向应力相对另外2个应力很小, 可以忽略, 即3= 0。假定钢管为理想弹塑性材料, 由第四强度理论有

考虑钢管截面平衡, 有

将式(10)代入式(9)可得

设c1、c2分别为外围混凝土和核心混凝土的截面积, 可得组合桩的轴压承载力

将式(8)、(11)代入式(12), 可得

可见, 轴压承载力是侧压力3的函数。为了求得轴压承载力的极值u, 令式(13)对侧压力3的导数等于0, 有

式(14)中,3′为对应于轴压极限承载力u的侧压力。

将式(14)代入式(13)中, 并取= 4, 令钢管混凝土的套箍指标, 经整理可得到轴心压力作用下组合桩配箍率不小于临界配箍率时的承载力计算公式为

3 配箍率小于临界配箍率时, 轴压承载力的计算

在配箍率小于临界配箍率时, 桩破坏时核心混凝土还没有达到极限状态, 钢管对混凝土的约束作用不能充分发挥。这时将组合桩视为由混凝土、钢管和纵向受力钢筋3种元件组成的结构体系, 忽略其相互作用, 得到其轴压承载力计算公式为

u=c1c1+c2c2+s2y2+s3y3。 (16)

式(16)中,s3、y3分别表示组合桩的纵向钢筋面积和屈服强度。

4 实例验证

文献[9]和文献[10]进行了钢管混凝土核心短柱轴压承载力的试验研究。由于组合桩可不考虑桩长对轴压承载力的影响, 其试验数据可以用来校核本文公式的正确性。组合桩分别采用文献[9]和文献[10]的参数, 利用本文方法计算的组合桩轴压承载力与文献[9]和文献[10]的实验结果进行比较, 结果如表1所示。本文计算结果和文献的实验结果比值的最大值为1.04, 最小值为0.95, 平均值为1.015, 标准差为0.037, 因此, 本文结果与文献结果吻合良好。

表1 本文方法计算结果与已有文献实验结果的比较 试件编号实际配箍率/%临界配箍率/%本文结果Nu/kN文献结果N/kN结果比值N/Nu 式(15)式(16) CDCFT1-1112 6552 663[9]1.00 CDCFT1-2112 7232 653[9]0.97 CDCFT1-3112 6262 633[9]1.00 CDCFT2-10.841.103 3183 451[9]1.04 CDCFT2-20.841.103 4283 515[9]1.03 CDCFT2-30.841.103 3043 615[9]1.09 YZ10.540.916 4576 597[10]1.02 YZ20.540.916 6256 845[10]1.03 YZ30.540.916 7426 954[10]1.03 YZ40.540.686 4386 096[10]0.95 YZ50.540.806 6646 751[10]1.01

5 结论

为了解决基础工程中的“胖桩”问题, 提出了一种新型的组合桩形式。在普通钢筋混凝土桩内部设置沿桩身纵向连续的圆钢管, 由于桩身内部圆钢管限制了核心混凝土的横向变形, 形成了所谓约束混凝土, 圆钢管在改善混凝土变形性能的同时, 提高了混凝土受压承载力, 因此桩身轴压承载力大于钢管和混凝土二者承载力的总和。这种新型的组合桩形式充分发挥了钢管和混凝土2种材料的性能, 是一种经济效益好, 技术先进的结构形式。

根据组合桩配箍率和临界配箍率的相对大小, 组合桩有2种破坏形式: 当配箍率小于临界配箍率时, 组合桩破坏始于外围混凝土破坏, 此时核心混凝土并末达到极限状态; 当配箍率不小于临界配箍率时, 组合桩破坏时核心混凝土和外围混凝土均达到极限状态。计算组合桩轴压承载力时, 要根据不同的破坏形式采用不同的计算方法。本文根据组合桩不同的破坏形式, 推导了组合桩在轴心压力作用下的承载力计算方法。实例验证结果表明, 本文计算结果与文献的实验结果吻合良好。本文计算方法形式简单, 物理意义明确, 便于实际工程应用。

[1] Zhang Dongdong, Lv Yaru, Liu Hanlong, et al. An analytical solution for load transfer mechanism of XCC pile foundations [J]. Computers and Geotechnics, 2015, 67: 223–228.

[2] Tourlonias Michel, Bueno Marie-Ange, Bocquet Romain, et al. Study of the friction mechanisms of pile surfaces: Measurement conditions and pile surface properties [J]. Wear, 2015, 328: 100–109.

[3] Hong Y, Soomro M A, Ng C W W. Settlement and load transfer mechanism of pile group due to side-by-side twin tunneling [J]. Computers and Geotechnics, 2015, 64: 105–119.

[4] Soomro M A, Hong Y, Ng C W W, et al. Load transfer mechanism in pile group due to single tunnel advancement in stiff clay [J]. Tunnelling and Underground Space Technology, 2015, 45: 63–72.

[5] Fan Haijian, Liang Robert. Importance sampling based algorithm for efficient reliability analysis of axially loaded piles [J]. Computers and Geotechnics, 2015, 65: 278–284.

[6] Liang Fayun, Song Zhu. BEM analysis of the interaction factor for vertically loaded dissimilar piles in saturated poroelastic soil [J]. Computers and Geotechnics, 2014, 62: 223–231.

[7] Yang Lijun, Liu Shaobin, Sun Jin. Analysis of vertical bearing characteristic of single piles with load transfer method [J]. Electronic Journal of Geotechnical Engineering, 2015, 20(10): 4 197–4 206.

[8] Li Zheng, Kotronis Panagiotis, Escoffier Sandra. Numerical study of the 3D failure envelope of a single pile in sand [J]. Computers and Geotechnics, 2014, 62: 11–26.

[9] 聂建国, 赵洁, 柏宇, 等. 钢管混凝土核心柱轴压极限承载力[J]. 清华大学学报(自然科学版), 2005, 45(9): 1153– 1156.

[10] 蔡健, 谢晓锋, 杨春, 等. 核心高强钢管混凝土柱轴压性能的试验研究[J]. 华南理工大学学报(自然科学版), 2002, 30(6): 81–85.

(责任编校: 江河)

The axial bearing capacity of a new composite pile

Yin Hang, Fu Rui, Luo Mei, Jiang Jianlin, Yang Lijun

(College of Architecture and Civil Engineering, Hunan University of Arts and Science, Changde 415000, China)

In order to solve the problem of large diameter pile, a new type of composite pile is put forward. The composite pile used in this study is that the continuous circular steel tube along with the longitudinal pile section is arranged in reinforced concrete pile. The mechanical mechanisms of composite pile under axial compression are analyzed. By considering the restraint effect of the steel tube and stirrups, the critical state stirrup ratio of the outer concrete is derived. With the difference of the stirrup ratio, there are two kinds of failure modes as the pile is under axial compression. The calculation formula of the axial bearing capacity of composite pile is derived in the two failure modes. The average value of the calculated and experimental ratio value is found as 1.015, with the standard deviation of 0.037, which shows a good agreement between the calculated and the measured values.

confined concrete; composite pile; axial bearing capacity; critical stirrup ratio

10.3969/j.issn.1672–6146.2016.04.013

TU 473.1

1672–6146(2016)04–0054–04

杨立军, yanglj9601@163.com。

2016–06–22

国家自然科学基金(51268005); 湖南省普通高校教学改革研究课题([2014]247); 湖南省教育科学“十二五”规划课题([2014]005); 湖南省“十二五”重点建设学科(机械设计及理论) (2011[76])。