纵向数据下工具变量线性回归模型的经验似然推断

袁进义，杨宜平

（1.重庆大学经济与工商管理学院,重庆400030；2.重庆工商大学数学与统计学院,重庆400067）

纵向数据下工具变量线性回归模型的经验似然推断

袁进义1，杨宜平2

（1.重庆大学经济与工商管理学院,重庆400030；2.重庆工商大学数学与统计学院,重庆400067）

文章考虑纵向数据下工具变量线性回归模型，基于工具变量和二次推断函数方法，提出了回归参数的经验对数似然比统计量。在一些正则条件下，证明了所提出的经验对数似然比统计量渐近于标准卡方分布，由此构造兴趣参数的置信域。

纵向数据；工具变量；二次推断函数；经验似然；工作相关阵

0　引言

经典线性回归模型在研究响应变量与解释变量之间的关系时，往往假定解释变量是外生变量。基于该假定，采用最小二乘法可以获得回归系数无偏的和相合的估计。但是在大多实际问题的研究中，尤其在社会、经济等许多领域解释变量往往是内生的。如Angrist和Krueger[1]在研究教育对收入的影响时，教育是一个内生变量；Frankel和Romer[2]在考虑国际贸易对经济增长的影响时，国际贸易是一个内生变量。工具变量的引入有效地解决了内生解释变量所带来的问题。Angrist和Krueger[1]选择“出生季节”作为教育年限的工具变量，对收入水平建立工具变量线性回归模型来分析教育对收入的影响；Frankel和Romer[2]使用“地理因素”作为工具变量来解决国际贸易对经济增长的促进作用所面临的内生解释变量的问题。关于工具变量回归模型的相关研究已有大量文献。Basmann[3]提出了两阶段最小二乘法估计工具变量线性回归模型中的回归系数；Buse[4]研究了工具变量估计的偏差问题；Chamberlain和Imbens[5]讨论了工具变量随机效应模型的估计问题；张卫东[6]讨论了线性模型中的测量误差问题与工具变量方法；胡毅和王美今[7]提出了工具变量估计的最优工具变量选取方法。

上述文献都是在独立数据下讨论工具变量线性回归模型的估计问题。在分析实际问题时，往往会遇到纵向数据。当前，关于纵向数据下工具变量回归模型的研究很少。因此，本文考虑如下纵向数据工具变量线性回归模型：

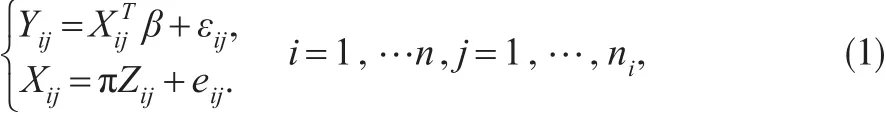
其中Yij是响应变量,Xij是p×1内生变量，即E(Xijεij)≠0，β是p×1未知参数，Π为p×k维未知参数矩阵，εij为模型误差，Zij是k×1工具变量，与解释变量Xij相关，且与模型误差εij不相关，即满足

E(Zijεij)=0且E(Zijeij)=0，i=1，…n，j=1，…，ni

本文的目的是利用0wen[8]提出的经验似然方法研究模型(1)中回归参数β的置信域的估计问题。关于该方法的相关研究参见文献[9-10]。为了处理模型中纵向数据的组内相关性，我们提出了基于工具变量和二次推断函数法的经验对数似然比函数，并证明了所提出的经验对数似然比函数渐近于标准卡方分布，进而构造回归参数β的置信区间。本文方法的优点在于：(1)利用二次推断函数法处理纵向数据的组内相关性，无需估计工作相关阵；(2)与传统的正态逼近方法构造置信区间相比，经验似然方法具有其独特的优势——不需要任何渐近方差的估计且区间估计的形状完全由数据决定。

1　回归参数的经验似然推断

由于模型(2)中Xi是内生变量，Zi是工具变量，则可以利用工具变量将内生变量进行分解。

由条件E(Zijeij)=0，结合模型(2)可得E(X|Z)=πZ。采用最小二乘法可得π的估计

因此，

采用Liang和Zerger[11]提出的广义估计方程方法，可以构造参数β的广义估计方程：

其中Vi是工作相关阵。在实际应用中Vi通常是未知的，且依赖有限维的讨厌参数，即将Vi进行分解成Vi=，其中Ai=diag(var(Yi1)，…，var(Yini))，R(ρ)是含讨厌参数ρ的工作相关阵。为了避免错误估计讨厌参数ρ对估计效的影响，利用Qu等[12]的思想，可将工作相关阵的逆R-1(ρ)表示为一些基矩阵的线性组合，即

其中ai(i=1，…，m)是未知的常数，Mi(i=1，…，m)是已知的基矩阵。一些常见的工作相关阵都可以由式(4)很好地逼近，具体参见文献[11]。将式(4)代入式(3)，得到如下估计方程：

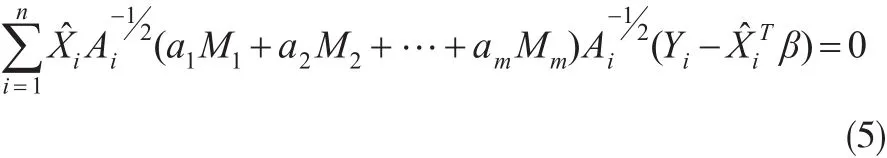
注意到估计方程(5)是辅助随机向量式(6)中元素的线性组合。如果β是参数真值，经简单计算可得利用该信息，可以构造回归参数β的经验对数似然比函数

由Lagrange乘子法，l(β)可表示为

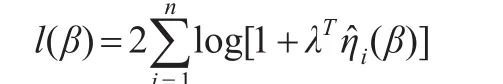
其中λ是ps×1向量，且满足

3　渐近性质

我们讨论经验对数似然比函数l(β)的渐近性质。为了得到定理1,需给出一些正则条件。

C1：参数β定义域是Rp上的一个紧集，真值β0是其一个内点。

C2:{} ni是有界的正整数列。

定理1：假定条件C1—C3成立，如果β是参数真值，则

基于定理1，可以构造β的1-α(0＜α＜1)的置信域：

Rα(β)

为了证明定理1，需要下面引理。

引理1：假定条件C1—C3成立，如果β是参数真值，则

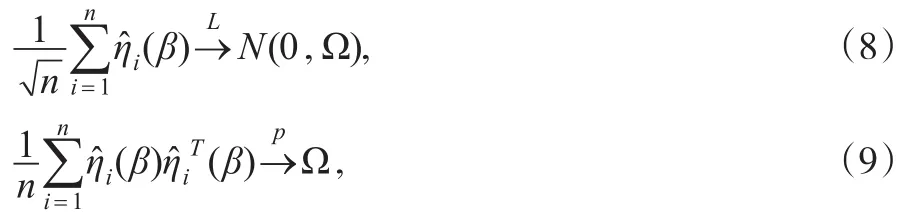
其中

其中Q2，s表示Q2的第s个分量。这就证得用Q3，s表示Q3的第s个分量，那么

定理1的证明：对l(β)进行Taylor展开，可得

上式结合引理1可得定理1。

4　结束语

本文针对解释变量是内生变量的线性回归模型，提出了基于工具变量的经验似然推断。在构造辅助随机向量时，为了消除纵向数据的组内相关性，对工作相关阵采用一些已知的基矩阵来逼近，避免了工作相关阵中讨厌参数的估计。进一步，为了避免内生变量对区间估计的影响，借鉴工具变量线性回归模型中两阶段最小二乘估计的思想，引入工具变量，利用工具变量将解释变量进行分解。在一些正则条件下，证明了所提出的经验对数似然比函数渐近于标准卡方分布。

[1]Angrist JD,Krueger A B.DoesCompulsory School Attendance Affect Schooling and Earning?[J].Quarterly Journal of Economics,1991, (106).

[2]Frankel J,Romer D.Does Trade Cause Growth?[J].American Eco⁃nomic Review,1999,89(3).

[3]Basmann R L.A Generalized Classical Method of Linear Estimation ofCoefficients in a Structural Equation[J].Econometrica,1957,(25).

[4]Buse A.The Biasof Instrumental Variable Estimators[J].Econometri⁃ca,1992,(60).

[5]Chamberlain G,Imbens G.Random Effect Estimator With Many In⁃strumentalVariables[J].Econometrica,2004,72.

[6]张卫东.线性模型中的测量误差问题与工具变量方法[J].统计与决策,2008,(8)

[7]胡毅，王美今.IV估计的最优工具变量选取方法[J].数量经济技术经济研究，2011,(7)

[8]Owen A B.Empirical Likelihood Ratio Confidence Intervals for a Sin⁃gle Function[J].Biometrika,1988,75(2).

[9]Xue L G.Empirical Likelihood for Linear ModelsWith Missing Es⁃ponses[J].JournalofMultivariate Analysis,2009(100).

[10]Zhao P X,Xue L G.Empirical Likelihood Inferences for Semipara⁃metric Instrumental Variable Models[J].Journal of Applied Mathe⁃maticsand Computing,2013,(32).

[11]Liang K Y,Zeger SL.Longitudinal Data Analysis Using Generalized LinerModels[J].Biometrika,1986,(32).

[12]Qu A,Lindsay B G,Li B.Improving Generalized Estimating Equa⁃tionsUsingQuadratic Inference Functions[J].Biometrika,2000,(87).

（责任编辑/易永生）

0212.7

A

1002-6487（2016）19-0073-03

国家自然科学基金资助项目(11301569)；国家社会科学基金资助项目（11CTJ004）；重庆市基础与前沿研究计划项目（cstc2015jcyjA00023）；重庆市教委科研项目(KJ1500614)

袁进义(1982—),男，湖北咸宁人，博士研究生，研究方向：知识管理。杨宜平(1981—),女，湖北荆州人，副教授,研究方向：非参数统计。