CVaR准则下基于损失厌恶的零售商订货决策问题
2016-12-09王利华
王利华
(西华师范大学商学院,四川南充637002)
CVaR准则下基于损失厌恶的零售商订货决策问题
王利华
(西华师范大学商学院,四川南充637002)
目前,多数学者在研究报童的利润最大化问题时,他们通常忽略了报童的风险偏好问题,或者是认为报童对于风险的偏好是中性的。然而,一些研究指出实践中的管理者在做订货决策时,其签订的订单会偏离于使利润最大化的最优订货量。一些学者通过引入行为偏好来解释这种决策偏见。文章在观察实际情形的基础下,引入报童的风险偏好和损失偏好。寻求的最优订货量需要满足两个目标:(1)零售商的剩余产品损失和缺货的机会成本之和最小;(2)零售商预期损失的条件风险最小。在一个给定的置信水平下,找到一个满足上述两个目标的最优订货量,帮助零售商优化订货决策。
报童模型;损失厌恶;风险厌恶;CVaR
0 引言
在供应链管理中,人们研究报童问题通常是研究一次性的业务决策,是指报童在面临不确定的市场需求下向供应商做出的订货决策。标准的报童问题已经得到广泛的研究,但是报童模型作为一个简单化的通用模型仍然在许多领域适用,并逐渐的扩展到更复杂的模型。本文中的报童模型是由一个供应商和一个零售商组成的一级供应链。
在传统的报童模型中,报童是风险中性的,报童通过预测市场需求,决策出一周期内的最优订货量,使自己的利润最大化。然而市场需求是不确定的,如果最优订货量高于实际的市场需求,那么报童就面临着遗留损失,即有多余的产品销售不出去。相反,如果最优订货量小于实际的市场需求,那么报童就会有缺货的损失,我们一般称之为缺货惩罚。因此,报童作出的订货决策要尽可能的与实际需求保持一致,避免以上的两种损失,使自己的预期收益最大化。
然而,最近的一些研究表明,零售商在实际决策中作出的订货量并不总是与预期的最优订货量保持一致,即偏离于利润最大化下的订货量。一些学者做过类似的实验,对于高利润和低利润的产品,零售商为使自己的收益最大化,出售低利润产品的零售商往往会作出高于最优订货量的订货决策,而出售高利润产品的零售商一般会作出低于最优订货量的订货决策。这种现象在报童模型中被成为决策偏见,于是许多学者便寻求可以解释这种决策偏见的原因,并得到了一些有趣的结论。
显而易见,在不确定的市场需求下,零售商面临着来自市场内部和外部的风险。例如,由于经济危机导致消费者需求的急剧下降,或者是供应产品成本的突然上升,都会使报童面临着重大的损失风险。于是,学者们观察到报童一个很明显的心理特征,相对于利润最大化的目标,报童对使自己的损失最小化更加敏感。事实上,报童偏离于最优订货量的订货决策,正是由于其更加关注损失的规避。查尔斯和韦伯斯特(2009)将损失厌恶引入报童模型的问题中,表明如果对缺货的惩罚是持续存在的,一个风险厌恶的报童将比风险中性的报童订货更多或更少,这刚好证明了在报童模型中决策偏见的存在。Shapira在1986年对50个美国的高层管理者作过采访,MacCrimmon和Wehrung在1996年对509个美国和加拿大的高层管理者进行问卷调查,分别得出了报童模型中的决策偏见是与损失厌恶密切相关的。在目前的文献中,已开始有部分的学者将认知心理学的偏好理论引入报童模型中,并取得了很好的效果。对于关注报童模型的损失厌恶问题相对较少,本文正是想通过损失厌恶这一视角,来研究报童模型的扩展型问题。
区别于传统报童模型中追求利润最大化的动机,本文中的报童由于个人的有限理性和心理偏好,更多的是关注损失最小化。在随机的市场需求下,报童对损失的厌恶,会做出使预期损失最小化的最优订货量。报童的预期包括剩余产品损失和缺货的机会成本,剩余产品的损失与回购价格相关,缺货的机会成本与批发价格和零售价相关,同时这两者直接受市场需求变化的影响。由于需求的随机性,零售商在预期损失最小化下做出的最优订货量有可能使自己的实际损失更大。
在考虑零售商的损失厌恶时,由于其实际损失与市场需求是息息相关的,所以不能忽视零售商面临的市场风险。在本文中,我们假定零售商的风险偏好时风险厌恶的,实际情况下大多数都是如此。CVaR是一种常用的风险度量工具,因此我们用CVaR来研究零售商面临损失的风险值。给定一个置信水平α,可以得到一个使预期损失风险值最小的最优订货量。
综上所述,在预期损失最小化和预期损失风险值最小化的条件下分别可以得到一个最优订货量。但是,只有将两者结合起来,才能得到一个更优的订货量。本文引入一个损失厌恶系数λ,表示零售商对预期损失的重视程度,相当于分配给预期损失的权重系数,1-λ则表示零售商分配给预期损失条件风险值的权重系数。通过损失厌恶系数调整后的预期损失可表示为:

在不同的损失厌恶系数下,说明零售商对预期损失不同的重视程度,并可得到一个最优的订货量。通过λ的调整,可以更好的参照零售商的心理偏好,帮忙零售商做出更优化的订货决策。
1 模型假设
本文研究的报童问题是单一的供应商和单一的零售商在单一周期里的订货决策问题。在传统报童问题中,一般是不考虑缺货惩罚的,因此零售商关于损失厌恶的心理容易被忽视。市场需求是随机的,零售商基于市场需求的预测向供应商订货,供应商做出回应与零售商签订合同。
1.1研究假设
在零售商和供应商的订货契约中,零售商拥有主动权。本文更是从零售商的心理偏好出发,以零售商的个体利益为度量标准,对零售商的订货量进行优化决策。为剔除相关因素的干扰,直接研究零售商在损失厌恶和风险厌恶心理下的决策行为,本文作出如下四点假设。
假设1:市场需求是不确定的,为一随机变量,且其密度函数和分布函数均存在。
假设2:供应商的生产能力是充足的,零售商根据需求预测与供应商签订订单,供应商能够满足所有的订货量。即在考虑零售商的风险来源时,不用考虑供应商供货不足的问题,零售商唯一需要考虑的风险是来自市场的需求变动。
假设3:供应商的批发价不随订货量的变动而变动,零售商的零售价格也不受市场需求量的影响,假设供应商的批发价和零售商的零售价均为常量。
假设4:零售商不仅关注市场风险,更关注回购多余产品和缺货惩罚下的机会成本,在平衡二者之间制定最优订货量。
1.2建立模型
本文研究的报童问题可以描述为:在一个单周期的销售季度内,一个零售商以批发价c从供应商处订购所销售的产品,然后以单位零售价r销售给顾客,零售商对于风险是态度是厌恶的,同时零售商的目标是追求预期损失的最小化。假设实际的市场需求x为随机变量,零售商卖剩的产品可以以回收价格s回购,且当零售商缺货时会面临缺货惩罚,单位产品的机会成本为p。
本文需要用到的符号为:
x—零售商面临的市场需求,为随机变量,其密度函数和累积分布函数分布为f(·)和F(·);
q—零售商的订货量;
r—产品的零售价格;
w—供应商的批发价格;
s—剩余存货的回购价格;
p—缺货惩罚的机会成本;
P(q)—零售商的销售利润;
L(q)—零售商的销售损失;
α—条件风险的置信水平;
λ—损失厌恶系数,λ和1-λ分别是分配给预期损失和条件风险值的权重;
E(l)—零售商调整损失系数后的销售损失。
零售商做出订货决策,在订单q下的销售利润为:

在订单q下的预期损失为:

(1)和(2)均为零售商在风险中性下的销售利润和预期损失,而本文要考虑零售商的风险偏好,引入CVaR条件风险值,调整后的最小化预期损失为:
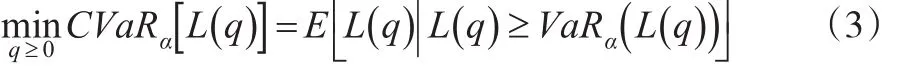
2 模型分析
在单一供应商和单一零售商组成的报童模型中,市场需求是一个随机变量,其密度函数和累积分布函数分布为f(·)和F(·)。在本文中,可以设定r≥w≥s,且F(0)=0,F(+∞)=1。F(·)是单调递增函数,其反函数是存在的。聪明的零售商会对顾客市场进行准确预测,并尽可能满足市场需求以获得最大化的利润。整个销售市场中只有一个零售商,不存在零售商之间的相互竞争行为,同时供应商的批发价和零售商的零售价都是固定不变的。零售商最大的动机是追求预期损失的最小化,其实际损失可表示为:

2.1损失厌恶下的最优订货量
在随机的市场需求下,零售商是不能准确计算出自己的实际收益或实际损失,所以零售商是基于需求预测和自己的心理偏好做出的订货决策。在存在剩余品回购和缺货惩罚的情况下,零售商使预期损失最小化的订货量需满足的条件为:

定理1因此,根据(2)和(4)可得到最优的订货量为


定理1表示为使零售商预期损失最小化的订货量,并且表明零售商的预期损失和缺货的机会成本p、批发价格w及回购价格s是相关联的。在本文中,我们可以假定缺货的机会成本p=r-w。那么最优订货量还可以表示为:

推论1由(5)可知,对于p≥0,s≥0,w≥0,最优订货量q*0随着缺货成本p和回购价格s单调递增,随着批发价格w单调递减。
通过推论1,最优订货量q*0随着缺货成本p和回购价格s单调递增,随着批发价格w单调递减。在实际的订货决策中,当缺货的机会成本较大的,零售商会更加倾向通过增加订货量来避免缺货惩罚。同时,如果零售商剩余产品的回购价格较高时,零售商的剩余产品损失就会降低,零售商就会增加订货量,在满足市场需求上更有保障。显而易见,如果批发价格较高,那么利润空间就会变小,零售商的剩余产品损失变大,所以零售商会降低订货量。
在上面,我们获得了使预期损失最小的最优订货量。然而,仅仅考虑零售商的损失厌恶偏好是不够的,零售商的预期损失不仅与缺货的机会成本p、批发价格w及回购价格s相关,也和市场需求相关。因此零售商在损失厌恶下做出的订货决策也是存在风险的,我们在接下里的研究模型中考虑零售商的风险厌恶偏好,帮助零售商做出更优的订货决策。
2.2风险厌恶下的最优订货量
由于市场需求的不确定,零售商在损失厌恶下做出的最优订货量有可能造成更大的损失,为了降低这种风险,零售商有必要调整自己的订货决策。在不同的市场环境下,零售商所面临的风险是不同的,这里只考虑零售商面临需求变化的风险。在不确定的报童模型中,CVaR是度量风险的一种有效工具。本文中,我们采用CVaR理论来控制零售商所面临的潜在风险,分析在α置信水平下风险最低的最优订货量。对于一个给定的置信水平α下,有关预期损失L(q)的风险值α-VaR为:

同时,在置信水平α下,对于零售商预期损失的条件风险值α-CVaR为:

对比(7)和(8),CVaR度量方法更加关注于预期损失的最小化。在置信水平α下,使用CVaR度量方法可以保障零售商在更大的可能下获得使预期损失最小的订货量。因此,接下来需要分析使CVaRα[L(q)]最小的订货量,即:

定理2零售商在风险厌恶偏好下的最优订货量为:

不难发现,推论2、推论3与推论1的结论是一致的。即当缺货的机会成本p和回购价格s增加时,零售商由于对风险的厌恶,会增加订货量。

2.3平衡预期损失和预期损失CVaR下的最优订货量
CVaR是很好的风险度量工具,然而使用CVaR仍然有些限制。相比于VaR,CVaR更加关注零售商所承受的风险,而忽略了零售商本身损失的大小。Gotoh和Takana在2007年在研究引入CVaR的扩展报童模型,通过平衡预期受益和条件风险值做出订货决策。由于本文中研究的零售商关注预期损失甚于预期受益,所以我们试图将预期收益和CVaR结合起来,通过平衡预期损失和条件风险值。为实现这一目标,我们假定

其中,λ∈(0,1)表示零售商对于损失厌恶的权重,即相比于预期损失的条件风险值CVaR,零售商认为对损失的规避更加重要。在算式(12)中,λ越大,表明零售商对损失更加关注。算式(12)很好的将零售商的损失厌恶和风险厌恶都考虑进来,接下来可得出在此模型下零售商的最优订货量。
定理3对于损失厌恶和风险厌恶的零售商,如果满足



事实上,定理1和定理2都可以看作是定理3的特殊情况,即当λ=1和λ=0时。
零售商在平衡预期损失和预期损失的条件风险值时,最优订货量均随着缺货成本p和回购价格s单调递增。定理3的这两个推论与定理1和定理2相似,但是对于α∈(0,1)和λ∈(0,1),最优订货量的变动情况未知。
2.4数值分析
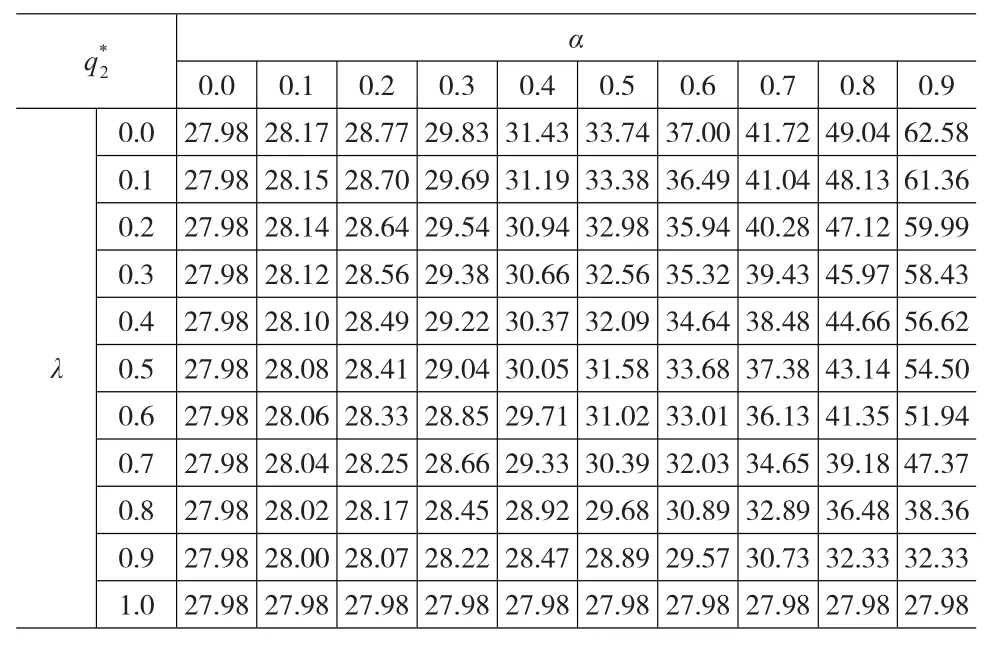
在上述的模型分析中,我们得到了一些定理和推论。于是,我们给出数值验证零售商在损失厌恶和风险厌恶下的最优订货量。我们假定市场需求x符合指数分布e(0.02),令w=5,p=3,s=1,然后我们计算在给定不同的置信水平α和损失厌恶系数λ下,零售商的最优订货量。得出的数值,如下表中所示。
q*2 α λ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 0.0 27.98 27.98 27.98 27.98 27.98 27.98 27.98 27.98 27.98 27.98 27.98 0.1 28.17 28.15 28.14 28.12 28.10 28.08 28.06 28.04 28.02 28.00 27.98 0.2 28.77 28.70 28.64 28.56 28.49 28.41 28.33 28.25 28.17 28.07 27.98 0.3 29.83 29.69 29.54 29.38 29.22 29.04 28.85 28.66 28.45 28.22 27.98 0.4 31.43 31.19 30.94 30.66 30.37 30.05 29.71 29.33 28.92 28.47 27.98 0.5 33.74 33.38 32.98 32.56 32.09 31.58 31.02 30.39 29.68 28.89 27.98 0.6 37.00 36.49 35.94 35.32 34.64 33.68 33.01 32.03 30.89 29.57 27.98 0.7 41.72 41.04 40.28 39.43 38.48 37.38 36.13 34.65 32.89 30.73 27.98 0.8 49.04 48.13 47.12 45.97 44.66 43.14 41.35 39.18 36.48 32.33 27.98 0.9 62.58 61.36 59.99 58.43 56.62 54.50 51.94 47.37 38.36 32.33 27.98
在表中,当α=0,即只考虑零售商的损失厌恶偏好时,有唯一的最优订货量=27.98。当λ=0时,在不同的置信水平下,零售商的最优订货量不同。可以看出,最优订货量随着置信水平α单调递增,随着损失厌恶系数λ单调递减。
3 结论
传统的报童模型中,研究对象主要是风险中性下的报童,一般是满足利润最大化下做出的最优订货量。然而,实际中的订货决策中,零售商的订货量往往会偏离于预期利润最大化下的最优订货量,学者一般称为决策偏见。目前,大多数有关报童问题的研究对象,都已经从简单的经典报童模型扩展为稍复杂的报童模型,以更加贴近实际的市场情况。在大量的文献中,学者们引入了行为学和认知心理学来解释零售商的决策偏见,从公平偏好、风险厌恶、损失厌恶、前景理论、锚定理论以及有限理性等行为因素研究对报童模型中运作决策从产生的影响。本文的创新点在于,通过引入CVaR,考虑了零售商的损失厌恶和风险厌恶两种心理偏好,来解释零售商在订货时产生的决策偏见问题。
本文假定的报童模型中,剩余产品损失和缺货惩罚是与市场需求相关的,即在随机的市场需求下,零售商会面临着需求风险。所以在文中,我们通过CVaR准则来度量零售商面临的损失风险。在本文的模型建立中,分别计算出了在预期损失最小化和损失的条件风险值最小化的最优订货量,且表明在一定条件下最优订货量随着回购价格和缺货的机会成本单调递增。最后,我们引入损失厌恶系数λ平衡了预期损失和CVaR,得到调整后的最优订货量。调整后的最优订货量不仅与批发价格和销售价有关,也和损失厌恶系数相关,通过调整损失厌恶系数,可以得到不同的最优订货量。
本文的结果是有参考价值的,在考虑了损失厌恶系数之后,可以更好的模拟零售商的心理偏好。同实际情况相参照,如果损失厌恶系数较大,那么该零售商具有更大的损失偏好,应该对实际的损失更加重视。那么该零售商在制定决策时,会使自己的实际损失在更大的可能性上最小。如果损失厌恶系数较小,那么该零售商具有更大的风险偏好,应该更多关注市场带来的损失风险,使自己面临的风险最低。在现实的供应链管理中,会有更多的因素影响报童的订货决策,本文为管理者在制定订货决策时,提供一个良好的决策参照模型。
[1]Artzner P,Delbaen F,Eber JM,et al.Coherent Measures of Risk [J].Mathematica Finance,1999,9(3).
[2]Eeckhoudt L,Gollier C,Schlesinger H.The Risk-averse(and prudent) Newsboy[J].ManagementScience,1995,41(5).
[3]SchweitzerM E,Cachon G P.Decision Bias in the Newsvendor Prob⁃lem With Aknowndem and Distribution:Experiment Alevidence[J]. Manag.Sci,2000,(46).
[4]褚宏睿,冉伦等.带有回购和缺货惩罚的损失厌恶报童问题[J].管理评论,2014,(11).
[5]侯阔林,洪志明.风险厌恶条件下竞争报童问题的二层规划模型[J].数学的实践与认识,2012,(2).
[6]刘俊山,基于风险测度理论的VaR与CVaR的比较研究[J].数量经济技术经济研究,2007,(3).
[7]徐志春,零售商风险厌恶情形下的契约协调,管理学报,2013,(12).
(责任编辑/易永生)
F724
A
1002-6487(2016)19-0045-04
国家社会科学基金一般项目(13BJL010)
王利华(1981—),女,四川江油人,博士,讲师,研究方向:电子商务、企业管理。
