多机动目标跟踪的BFG-GMPHD算法

赵斌，胡建旺，吉兵

（军械工程学院，石家庄050003）

多机动目标跟踪的BFG-GMPHD算法

赵斌，胡建旺，吉兵

（军械工程学院，石家庄050003）

针对高斯混合概率假设密度(GMPHD）滤波算法中的机动目标跟踪问题，提出BFG-GMPHD算法，扩展了GMPHD滤波算法的适用范围。算法利用最佳拟合高斯（BFG）分布来近似目标动态模型中的状态转移矩阵和过程噪声的协方差矩阵，实现了滤波器与不同动态模型的匹配；在对BFG分布进行递推时，引入了模型概率更新过程，解决了BFG仅依赖于先验信息的问题；并利用UKF算法对GMPHD的高斯分量进行递推，使得算法能处理量测方程为非线性的情况。仿真实验表明，BFG-GMPHD算法能快速匹配目标模型的变化，实现对多机动目标的有效跟踪，准确估计出目标的数目和状态。

概率假设密度，高斯混合，机动目标，最佳拟合高斯，模型概率更新

0 引言

在多目标跟踪中，一些传统数据关联算法，如联合概率数据关联（JPDA）和多假设跟踪（MHT）等，需要建立目标与量测值之间的对应关系［1］，随着杂波和目标数的增加，会导致计算量的指数增长［2］。针对这一问题，Mahler［3］提出基于随机集理论的概率假设密度（PHD）滤波算法，避开了复杂的数据关联问题，算法能够处理杂波、虚警环境下的目标跟踪问题。PHD的实现方式［4］主要有序列蒙特卡洛（SMC）和高斯混合（GM）两种形式，Vo等［5］提出的高斯混合实现方式能够提供解析解，并且具有计算量小、实现简单的优点，使得GMPHD滤波算法成为多目标跟踪领域研究的热点。然而，基于随机集的多目标跟踪算法针对的是整个多目标状态随机集，并不区分个体目标的运动特性，当目标发生机动时，不能有效识别出每个目标的机动情况。对于机动目标的跟踪问题，文献［6-9］提出利用BFG分布来近似目标的动态模型，但是在对动态模型近似时仅利用了先验信息，对新获得的有用量测信息缺乏有效利用，在BFG递推时可能会导致模型概率不能匹配目标的实际运动模型。

针对机动目标跟踪问题，本文将BFG算法和GMPHD滤波器相结合，提出了BFG-GMPHD滤波算法。算法用BFG分布来近似动态模型中的状态转移矩阵和过程噪声的协方差矩阵，使得目标在不同运动模式下具有相同的均值和协方差矩阵。同时，文章对BFG算法作出改进，借鉴交互多模型算法中的模型匹配滤波和模型概率更新过程，利用新获得的量测对BFG近似中的模型概率进行更新，解决了模型概率递推仅依赖于先验信息的问题；并用UKF对高斯分量进行递推，可用于处理量测方程非线性的情况。

1 PHD滤波器

基于随机有限集的PHD滤波算法［10］把目标的状态和量测看作是随机的单目标状态集合和单传感器量测集合，从而将多目标跟踪问题转化为集合意义上的单目标跟踪问题，避免了从量测到航迹的关联问题。PHD滤波器主要通过PHD的预测和更新来实现递推，其预测的PHD可表示为

2 BFG算法

最佳高斯拟合（BFG）算法［6］是一种针对跳变马尔可夫线性系统（JMLS）的性能估计方法，此处的线性系统仅指目标的动态模型需要为线性，而与量测方程无关。它用BFG分布来近似目标运动模型中的状态转移矩阵和过程噪声的协方差矩阵，使得近似前后目标在不同模型下具有相同的预测均值和协方差矩阵。假设系统模型如下：

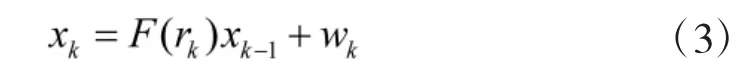
其中，xk∈Rn表示目标在k时刻的状态，F（rk）表示模型rk下的状态转移矩阵，记为Fr，wk为加性白噪声，满足零均值高斯分布，其协方差阵为Qk，模型转移矩阵为πij=Pr（rk=j|rk-1=i）。

BFG近似是将式（3）用一个BFG分布进行替换

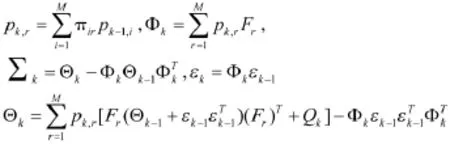
其中，pk，r表示在［k-1，k）期间模型r有效的概率。εk和Θk分别表示状态xk的均值与协方差。

该方法存在的问题在于对模型概率的处理仅依赖于先验信息，而忽略了量测信息对系统的影响，随着递推的进行，模型概率会出现收敛的情况，使得滤波器不能良好匹配目标的运动模型，致使滤波器发散。为了解决这一问题，本文借鉴交互多模型中的模型匹配滤波和模型概率更新过程［11-13］，在得到量测信息后，利用其对各模型进行匹配滤波，在当前量测作用下，求出对应于每个模型的似然函数，并利用似然函数对模型概率进行更新，从而保证了随着递推的进行，匹配度最高的模型具有最大的模型概率，使得滤波器能始终匹配目标的运动模型。各模型的似然函数表示如下：

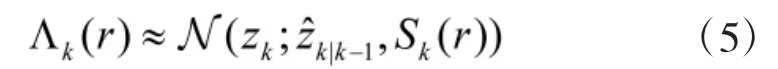
再对模型概率进行更新

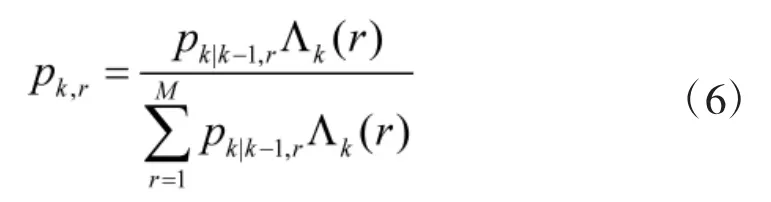
3 BFG-GMPHD算法

在利用GMPHD滤波算法时，除了要满足PHD滤波器常用的假设外，还需要满足以下假设：单目标的马尔可夫转移密度和似然函数都是线性高斯的，目标的存活概率ps为常数，检测概率pD为常数，目标新生和衍生过程的PHD都是高斯混合形式的。则在任意给定时刻k，GMPHD的形式为

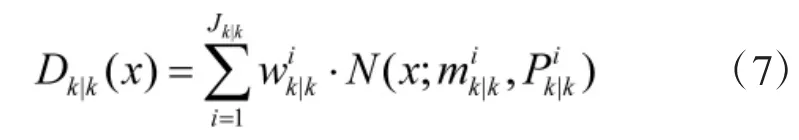
其中，Jk|k表示高斯分量数目，wik|k表示分量权值，μik|k表示分量均值，Pik|k表示分量协方差。通过BFG算法求得Φk和∑k后，用其替换GMPHD滤波器中的状态转移矩阵和过程噪声协方差矩阵，得到BFG-GMPHD滤波算法，并利用UKF对GMPHD的高斯分量（wik|k，mik|k，Pik|k）进行递推，使得算法具备处理非线性量测方程的能力，假设系统方程如下

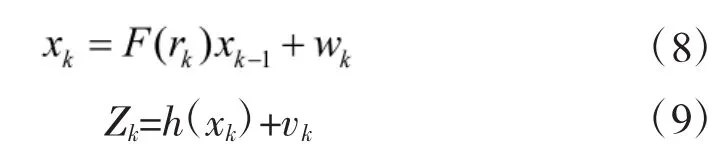
则算法的具体实现过程为：

①初始化。假设在0时刻，初始化为具有J0个分量的混合高斯分布，即

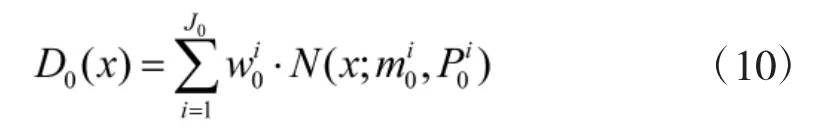
②预测。在预测阶段，新生目标密度和衍生目标可分别用高斯混合形式表示为：

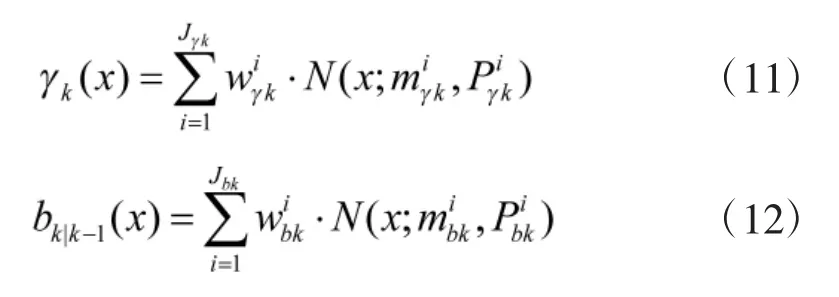
其中，Jγk和Jbk分别为目标新生和目标衍生密度的高斯分量总数。

由此可得预测PHD函数为：

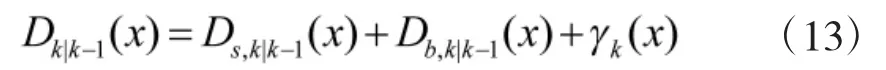
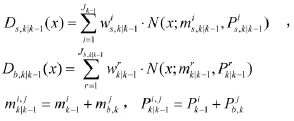
BFG的递推式为：

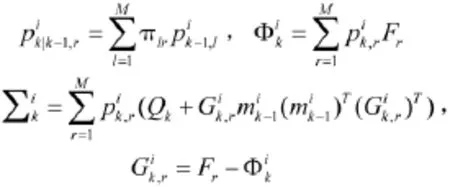
利用不敏变换产生2L+1个样点及其对应的权值

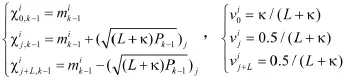
则预测参数的递推形式为：

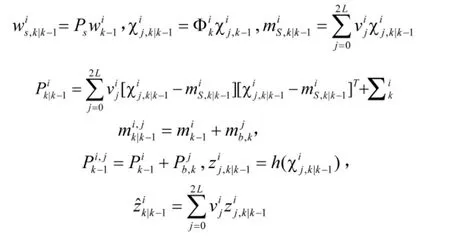
于是，预测PHD可写成：

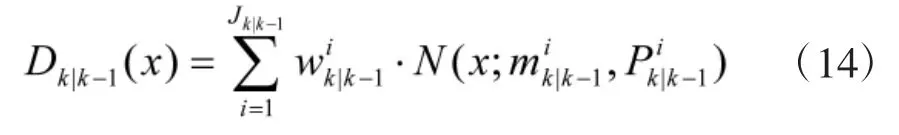
③更新。在更新阶段，其PHD可记为

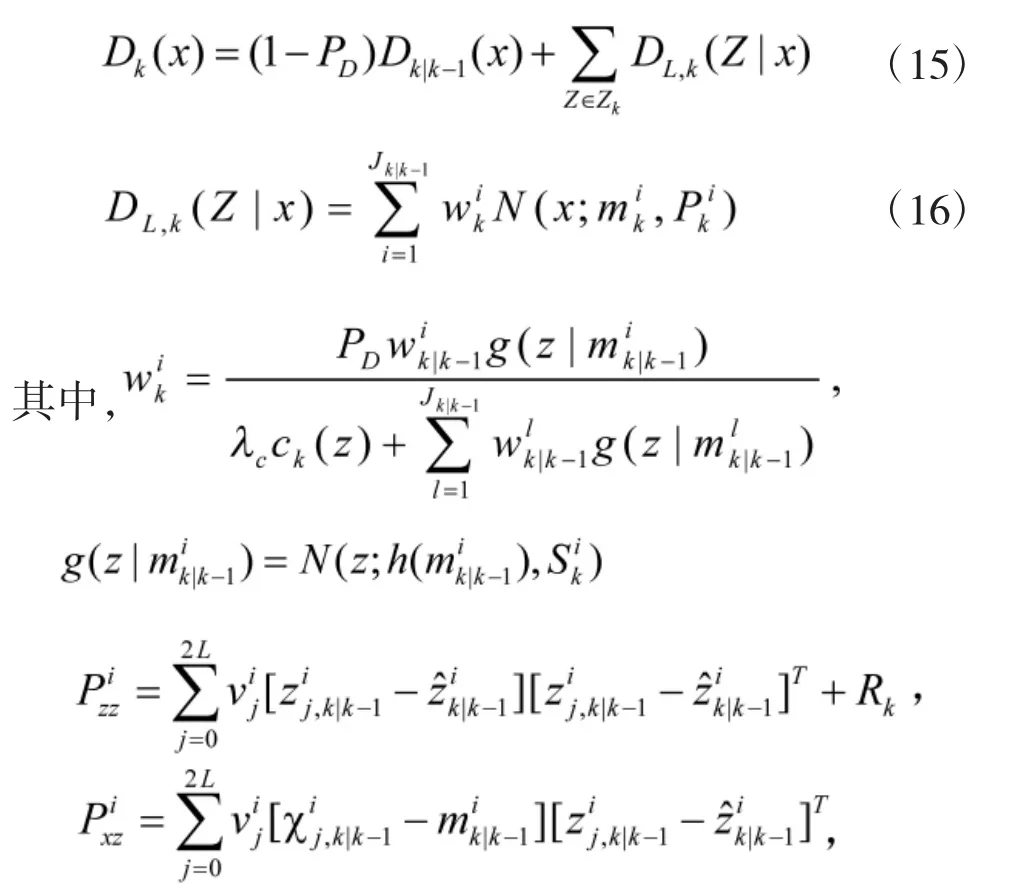
BFG中模型的似然函数为：

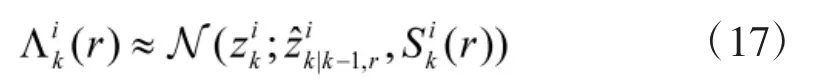
需要特别注意的是，该过程中的量测预测、残差协方差矩阵和协方差矩阵预测与前文GMPHD递推中的预测值和残差阵是有区别的。前文主要是在BFG近似的基础上对其进行递推，相当于在“单模型”形式下实现滤波，而在BFG的模型概率更新过程中，需要针对每个模型求出相应的似然函数，因此，在BFG模型概率的更新过程中，量测预测、残差协方差矩阵和协方差矩阵预测都要对应于相关模型，而不能直接利用GMPHD中的相应结果。

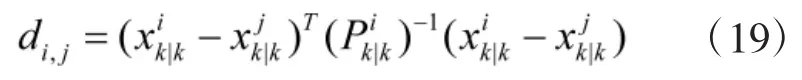
⑤数目与状态估计。在经过上述4个步骤后得到k时刻的高斯分量，将权值累加得到目标数目的估计值。再根据权值选择出相应的高斯分量对多目标的状态作出估计。

4 仿真验证

目标的监测区域为［-1 000 m，1 000 m］×［-1 000 m，1 000 m］，整个跟踪过程中设置了4个目标，待估计目标状态为其位置的二维坐标和相应的速度，表示为［xk，x˙k，yk，y˙k］T。假设杂波出现服从泊松分布，该过程中没有衍生目标出现。采样时间周期T=1 s，跟踪时长为50个采样周期。实验中利用CT模型作为目标的运动模型，通过改变模型中转弯速率w的值来实现目标运动模型的变化，目标分别在0 s～18 s时间段内以w=0.001做近似的直线运动，19 s～30 s以w=0.2做转弯运动，31 s～50 s以w= -0.15做转弯运动。状态转移矩阵，模型转移矩阵等参数设置如下

检测概率为PD=0.9，存活概率为Ps=0.9，杂波平均数为35，最大高斯数Jmax=100，修剪门限Up=10-5，合并门限m=5，模型概率初始值为p=［0.8 0.15 0.05］T。实验结果如图1～图5所示。

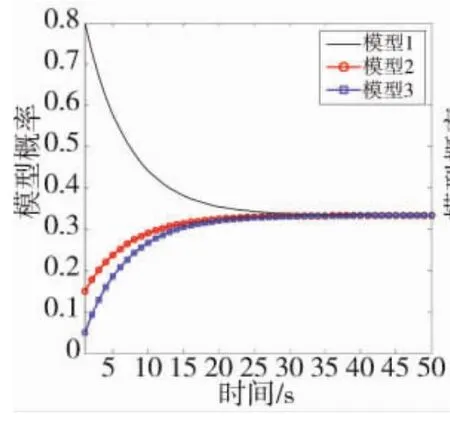
图1 未加更新过程的模型概率变化情况

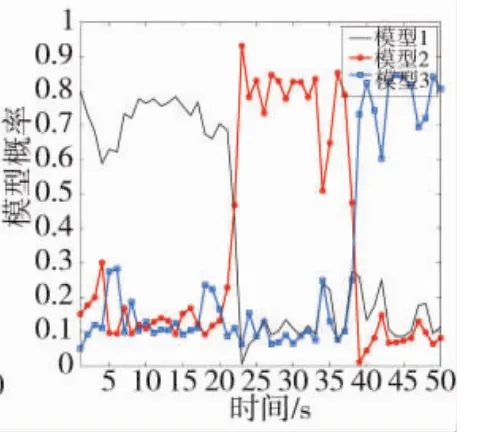
图2 加入更新过程后的模型概率变化情况

图3 多目标在x、y方向上的量测

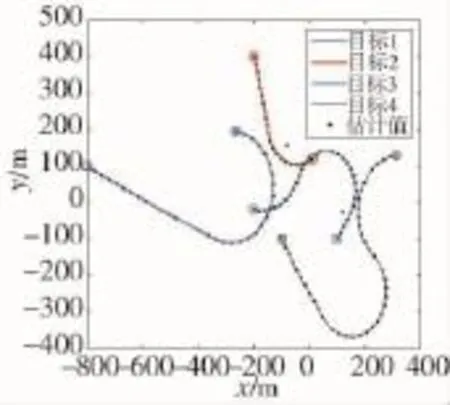
图4 多目标真实航迹及状态估计

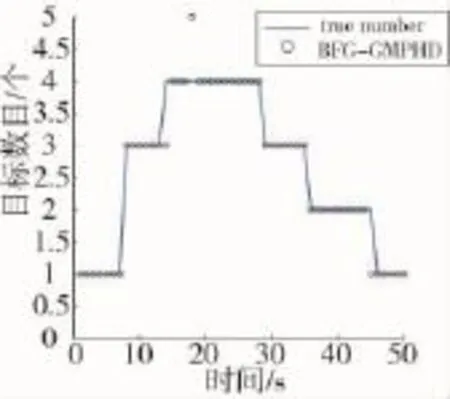
图5 目标数目估计

图1和图2分别给出了模型概率在有无更新过程的变化情况，由图1可以看出当不存在更多先验信息而对模型概率进行递推时，由于缺少更新过程，将会出现多个模型的概率收敛到同一值的情况，如果要实现对多目标的有效跟踪，需要提供机动时刻、机动水平等更多的先验信息。图2所示为加入模型概率更新过程后概率的变化情况，当目标发生机动时，通过更新后，模型概率能迅速跟踪目标动态模型的变化，从而将滤波器的参数调整为更加切合目标实际运动模型的状态，增强了滤波器的鲁棒性。

图3给出了目标在x和y方向上的量测值和源于真实目标的量测值随时间的变化情况，从图3中可以直观看出，目标所处的环境存在着大量的杂波干扰，源于真实目标的测量值与杂波的干扰值混叠在一起，难以区分，且目标数目随时间而变化。

多目标的真实航迹与状态估计结果可以从图4中得到，可以看出所提算法估计结果能准确反映出多目标位置，有效滤除杂波干扰，并且当目标实施机动时，也能实现稳定的跟踪。

图5是在不同时刻上多目标的真实数目以及经过BFG-GMPHD滤波器处理后的目标数目估计值。由图可知，BFG-GMPHD算法能准确估计出多目标数目。

5 结论

当目标发生机动时，GMPHD滤波器与目标实际动态模型的不匹配将导致滤波器的发散。本文针对跳变马尔可夫线性系统（JMLS），利用BFG方法来处理多模型的匹配问题，并将其与GMPHD结合，提出了BFG-GMPHD滤波算法，用以实现对机动目标的跟踪。在高斯混合框架下，采用BFG方法对目标的动态模型进行近似，通过模型概率的变化来体现目标模型的变化情况，并在模型概率的计算中引入交互多模型中的模型匹配滤波和模型概率更新过程，改善了BFG近似中模型概率仅依赖先验信息的问题。同时利用UKF对高斯分量进行递推，使得算法能处理非线性量测方程。

［1］韩崇昭，朱洪艳，段战胜，等.多源信息融合［M］.北京：清华大学出版社，2006.

［2］谭顺成，王国宏，王娜，等.基于PHD滤波和数据关联的多目标跟踪［J］.系统工程与电子技术，2011，33（4）：734-737.

［3］MAHLER R.Multitarget bayes filtering via first-order multitargetmoments［J］.IEEE Transaction on Aerospace and Electronic Systems，2003，39（4）：1152-1178.

［4］杨峰，王永齐，梁彦，等.基于概率假设密度滤波方法的多目标跟踪技术综述［J］.自动化学报，2013，39（11）：1944-1956.

［5］VO B N，MA W K.The gaussian mixture probability hypothesis density filter［J］.IEEE Transactions on Signal Processing，2006，54（11）：4091-4104.

［6］RISTIC B，HERNANDEZ M，FARINA A.A performance bound for maneuvering target tracking using best-fitting Gaussian distributions［C］//Proceeding of International Conference on Information Fusion，2005：1-8.

［7］BREHARD T，CADRE J P L.Closed-form posterior cramer-rao bound for a maneuvering target in the bearings-only tracking context using best-fitting gaussian distribution［C］//Information Fusion，2006 9th International Conference on.IEEE，2006：1-7.

［8］MORELANDE M，RISTIC B，HERNANDEZ M.A new best fitting gaussian performance measure for jump markov systems［C］//Information Fusion International Conference on，2008：1-6.

［9］LI W，JIA Y，DU J，et al.Gaussian mixture PHD filter for multiple maneuvering extended targets tracking［C］//2011 50th IEEE Conference on Decision and Control and European Control Conference（CDC-ECC），2011：2410-2415.

［10］蒋红旗，卢大威，刘本源，等.多源多目标统计信息融合［M］.北京：国防工业出版社，2013.

［11］占荣辉，张军.非线性滤波理论与目标跟踪应用［M］.北京：国防工业出版社，2013.

［12］王永生，范洪达.机动目标跟踪的IMM和IMMF-LS自适应滤波算法［J］.计算机仿真，2002，19（5）：48-52.

［13］郭志，董春云，蔡远利，等.时变转移概率IMM-SRCKF动目标跟踪算法［J］.系统工程与电子技术，2015，37（1）：24-30.

［14］DANIEL C，BA-NGU V.Convergence analysis of the gaussian mixture PHD filter［J］.IEEE Transactions on Singnal Processing，2007，55（4）：1204-1212.

［15］穆欣侃，徐德江，罗海波，等.基于新模板匹配的运动目标跟踪算法［J］.火力与指挥控制，2013，38（3）：22-26.

A BFG-GMPHD Algorithm for Multiple Maneuvering Targets

ZHAO Bin，HU Jian-wang，JI Bing
（Ordnance Engineering College，Shijiazhuang 050003，China）

In order to track maneuvering target with Gaussian mixture probability hypothesis density（GMPHD）filtering algorithm，the BFG-GMPHDalgorithm is proposed based on the best fitting Gaussian（BFG）algorithm which canrelax restrictions of the GMPHD filter algorithm.The proposed algorithm utilizes BFG distribution to approximate the state transition matrix and process noise covariance matrix oftarget kinematicmodel to match the filter with different kinematicmodel.The model probability update process is introduced into the recursion of BFG to solve the problem that therecursion of BFG is only determined by priori information；and the recursiveGMPHD Gaussian components is obtained by UKF algorithm which makes the algorithm have the ability to deal with nonlinear measurement equation.The simulation experiments show that the BFG-GMPHD algorithm can quickly match themodel probability and targetkinematic model，effectively track multiple maneuvering targets and accurately estimate targets number and state.

probability hypothesis density，Gaussian mixture，maneuvering targets，best fitting Gaussian，model probability update

TP212

A

1002-0640（2016）11-0192-05

2015-08-05

2015-10-10

赵斌（1990-），男，四川德阳人，硕士研究生。研究方向：信息融合。