基于集合交的欧式误差状态估计方法*

武宜川

（江苏自动化研究所，江苏连云港222061）

基于集合交的欧式误差状态估计方法*

武宜川

（江苏自动化研究所，江苏连云港222061）

基于集合交的欧式误差估计方法利用集合理论，根据已有的探测数据对目标的状态进行估计，在满足一定的条件下，计算目标状态估计集合。根据该集合确定状态的估计值以及估计的欧式误差范围。可以针对某一次具体的实验，计算目标的状态估计以及误差界。

目标状态，估计，欧式，集合

0 引言

对敌方运动目标位置的跟踪是军事装备情报指挥系统的重要工作之一，其核心是根据探测器获得的目标过去一段时间的空间位置的探测数据，对每个目标今后的空间位置进行估计。在状态估计领域中，卡尔曼滤波算法获得了较为广泛的应用，能够进行实时的递推计算，只需要获得当前的探测值和上一个周期的预测值就能进行状态估计。该理论应用的前提是需要获取相关的噪声特性和目标的运动模型，在统计意义下可以获得最优的状态估计值。但获得的状态估计值和对应的误差都是在统计意义下的。实际应用中往往是针对某一次具体的试验，给出明确的状态值以及误差估计。因此，提出了欧式误差估计方法，主要研究针对某一次具体试验，根据目标的运动模型，在欧式误差准则下的状态估计方法。所谓的欧式误差，是指估计值的绝对意义下的误差，而并非卡尔曼滤波统计意义的误差。该方法可以在某一次具体试验中，明确状态估计的误差值，为指挥员作出决策提供支撑。

1 问题描述

卡尔曼理论中认为每个探测数据都存在相应的探测噪声，欧式误差状态估计方法认为在每个探测数据附近都存在一个集合，使得被探测目标的真实位置是该集合中的一个元素，称该集合为该探测数据构成的探测集合，探测集合是一个包含目标真实位置的集合，一般是以探测数据为中心，边界是由若干倍的方差定义的直线或曲线构成的。由于目标的位置状态一定属于该集合，所以可以将探测集合视为目标在该时刻空间位置的限制条件。

卡尔曼理论认为目标状态在某一段时间内都是按照某种状态方程进行变化的。欧式误差状态估计方法看待目标运动的观点为：在一系列（建立在探测数据基础之上）的探测域的约束下，如果目标按某种运动模式运动，那么对于任何未来给定时刻t，都一定存在一个集合，使得目标在t时刻的空间位置一定在该集合内，称该集合为未来时刻t的预测集合。预测集合由目标的最大运动方程（即根据积累探测数据、探测误差界以及目标运动模型推算出目标在当前时刻最远运动到何处）和最小运动方程组成。结合目标的探测集合，可以最终确定目标的状态集合。通过这样的集合交集可以保证目标的真实位置必然位于该集合中。在该集合中选取中心点作为目标的状态估计值，并根据该点到集合边缘的距离确定该状态估计的欧式误差。

2 算法流程

2.1目标做匀速直线运动

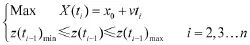
求解获得在ti时刻状态预测域的上界X（ti）max

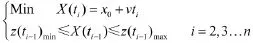
求解获得在ti时刻状态预测域的下界X（ti）min

根据状态预测集合［X（ti）min，X（ti）max］和探测域集合［z（ti）min，z（ti）max］的交集确定目标在tn+1时刻的状态集合，如果存在多个传感器探测，则可以根据各个传感器的状态集合交集进一步缩小集合范围，获得更为精确的状态估计结果。

其中，ti时刻的探测集合［z（ti）min，z（ti）max］是由前端探测传感器直接给出的，一般可由探测值以及传感器的标称值获得。根据获得的探测集合［z（ti）min，z（ti）max］以及目标的运动模型，如何计算目标的状态预测集合是比较关键的，这里首先给出目标运动最大方程和最小方程的解析表达式。

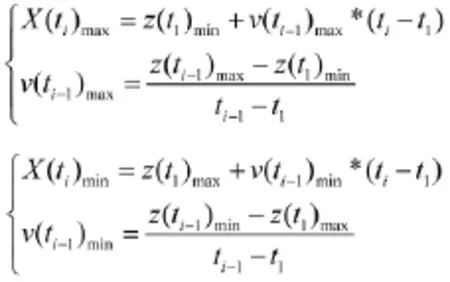
算法的迭代公式如下：

①t1时刻的探测域为［z（t1）min，z（t1）max］，其中t1时刻探测的最大值为，最小值为：。

②ti-1时刻的探测域为［z（ti-1）min，z（ti-1）max］，其中ti-1时刻探测的最大值为，最小值为。

③根据目标的运动模型选取t1和ti-1时刻的探测值确定ti时刻目标运动的最大方程，最大方程的表达式为：，其中：。

④根据目标的运动模型选取t1和ti-1时刻的探测值确定ti时刻目标运动的最小方程，最小方程的表达式为：，其中：。

⑤ti时刻的预测域为［X（ti）min，X（ti）max］。

⑥根据ti时刻的探测域和预测域确定状态集合为［S（ti）min，S（ti）max］，其中。

⑦根据状态集合为［S（ti）min，S（ti）max］确定状态值为，对应的欧式误差值为。

2.2目标做匀加速直线运动

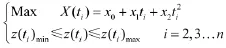
求解获得在ti时刻状态预测域的上界X（ti）max

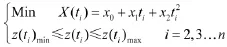
求解获得在ti时刻状态预测域的下界X（ti）minti时刻状态预测集合的计算公式如下：

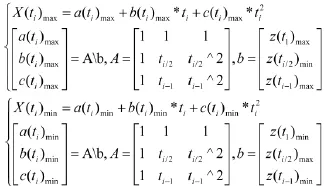
3 仿真结果与结论

3.1目标做匀速直线运动

仿真剧情：目标做匀速直线运动，目标初始位置坐标为（1 000，2 000），目标在X、Y方向上的速度分别为5 m/s、6 m/s，探测平台的位置为（0，0），探测平台在距离和方位上的探测随机误差分别为100 m、0.03 mrad。假设每个时刻获得的探测欧式误差为真实误差的1.2倍。采用基于集合的欧式误差估计算法得到的结果如图1、图2所示。

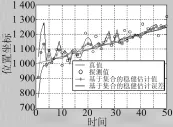
图1 匀速直线模型X方向上位置示意图

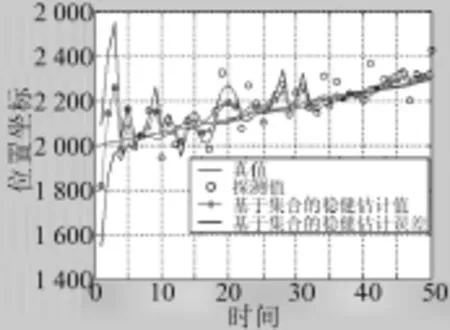
图2 匀速直线模型Y方向上位置示意图

3.2目标做匀加速直线运动

仿真剧情：目标做匀加速直线运动，目标在X、 Y方向上的运动模型为：，其中：X方向上的参数a=1 000，b=3，c=0.3，Y方向上的参数a=1 000，b=2，c=0.3。目标初始位置坐标为（1 000，2 000），探测平台的位置为（0，0），探测平台在距离和方位上的探测随机误差分别为100 m，0.03 mrad。假设每个时刻获得的探测欧式误差为真实误差的1.2倍。采用基于集合的欧式误差估计算法得到的结果如图3、图4所示。

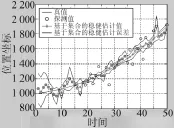
图3 匀加速直线模型X方向上位置示意图

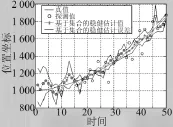
图4 匀加速直线模型Y方向上位置示意图

4 结论

通过上述仿真验证的结果可以看出，基于集合的欧式误差估计算法可以对目标的状态进行估计，并给出相应的误差结果。且给出的状态估计误差可以完全覆盖真值。

［1］SHEN X J，ZHU Y M，SONG E B，et al.Minimizing euclidian state estimation error for linear uncertain dynamic systems based on multisens or and multi-algorithm fusion［J］.IEEE TransactionsonInformationTheory，2011，57（10）：7131-7146，ISI：000295739000056.

［2］BAR-SHALOM Y，LI X R.Multitarget-multisensor tracking：principles and technique［M］.Storrs，CT：YBS Publishing，1995.

［3］SHEN X，ZHU Y，SONG L.Linear b-spline copulas with applications to nonparametric estimation of copulas［J］.Computational Statistics and Data Analysis，2008，52：3806-3819.

An Euclidian Error Estimation Algorithm for Setting Intersection

WU Yi-chuan
（Jiangsu Automation Research Institute，Lianyungang 222061，China）

The euclidian error estimation algorithm for setting intersection considers the problem of locating target by detected data，calculating the setting of target state estimation.Furthermore，computing the target state and the Euclidian state estimation error.The Algorithm can calculate the target state estimation and the Euclidian error for a certain experimentation.

target state，estimation，euclidian，setting

E911

A

1002-0640（2016）11-0045-03

2015-10-06

2015-11-19

国防“973”课题预研基金资助项目（61310102）

武宜川（1985-），男，江苏连云港人，工程师。研究方向：数据融合。