基于调频傅里叶变换的高速目标ISAR距离像算法*

罗文茂，崔应留

（1.南京信息职业技术学院通信学院，南京210023；2.南京审计学院工学院，南京211815）

基于调频傅里叶变换的高速目标ISAR距离像算法*

罗文茂1，崔应留2

（1.南京信息职业技术学院通信学院，南京210023；2.南京审计学院工学院，南京211815）

在大时宽带宽线性调频（LFM）体制高分辨逆合成孔径（ISAR）雷达中，目标高速运动将引起严重的回波多普勒色散，如果不消除该影响则不能正确成像。针对该问题，设计了一种通过调频傅里叶变换对目标脉内运动参数进行估计，补偿回波脉内走动得到目标距离像的方法。该方法首先估计脉内运动参数，初步补偿脉内走动，然后估计运动轨迹进一步精确补偿脉内走动，补偿脉内走动后通过包络对齐消除脉间走动，得到目标距离像。算法的主要过程在脉冲重复周期内进行，可以满足实时成像和参数估计的需求。

ISAR，调频傅里叶变换，线性调频，高速目标，脉内补偿

0 引言

逆合成孔径雷达（ISAR）常用线性调频信号（LFM）进行脉冲压缩，得到目标高分辨距离像。对于一些高速目标，如高超声速飞机、弹道导弹、航天飞行器等，速度在几公里到几十公里每秒之间，其距离走动在一个脉冲持续时间内将会跨越多个距离门，引起严重的距离色散。目标高速运动会引起脉间和脉内距离走动，对于脉间距离走动可以通过普通的包络对齐方法［1］处理。而对于脉内距离走动可以基于对运动参考点轨迹估计的方法实现［2］，也可以通过估计运动参数实现［3-5］。

调频傅里叶变换［6］是匹配傅里叶变换［7］的一种极坐标表示方法，对于线性调频信号的处理具有先天的优势。通过调频傅里叶变换可以得到线性调频信号的载波频率和调频率，而且是一种线性变换，和时频变换相比不存在交叉项。调频傅里叶变换和脉冲压缩一样，可以得到目标一维距离像，且两种方法的分辨力、抗噪能力一致。

本文提出一种基于调频傅里叶变换方法实现对高速目标脉内运动补偿算法。算法第1步利用调频傅里叶变换估计脉内运动参数，构造相位补偿函数初步补偿脉内走动；第2步通过调频傅里叶变换生成一维距离像，第3步根据距离像拟合运动轨迹，构造相位补偿函数精确补偿脉内走动；最后通过传统的脉冲压缩、包络对齐得到目标距离像。

本文由调频傅里叶变换构成的目标运动参数搜索算法和分数阶傅里叶变换算法［4-5］的运算量是基本相当的，并且由于调频傅里叶变换的计算量主要由参数搜索范围决定，所以在脉冲采样数N较大时比FRFT的计算量小。本文算法可以同时实现目标运动参数估计和成像，且算法的主体部分在脉冲持续时间内处理，可以保证成像的实时性。

1 算法原理

1.1调频傅里叶变换的定义

对于一个二次相位信号：

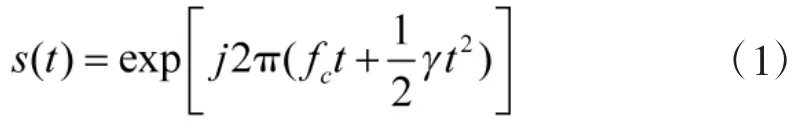
式中：载波频率fc和调频率γ是信号参数。

其调频傅里叶变换为［6］：

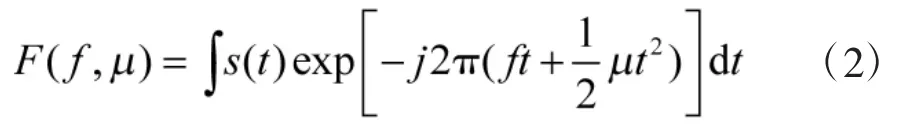
式中：f和μ是调频傅里叶变换的参数。

可以看出，在调频傅里叶变换生成的f-μ谱图中，当f=fc，μ=γ时，出现信号的相参积累峰值，即可以通过调频傅里叶变换得到二次相位信号的参数估计。

1.2基于调频傅里叶变换的脉内走动补偿

假设ISAR雷达发射脉冲重复周期Tp，带宽为B的线性调频（LFM）信号，第m个脉冲可以表示为：

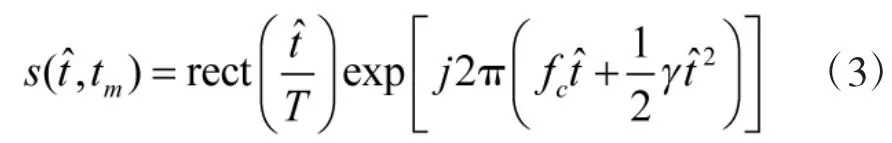
目标回波可以表示为：

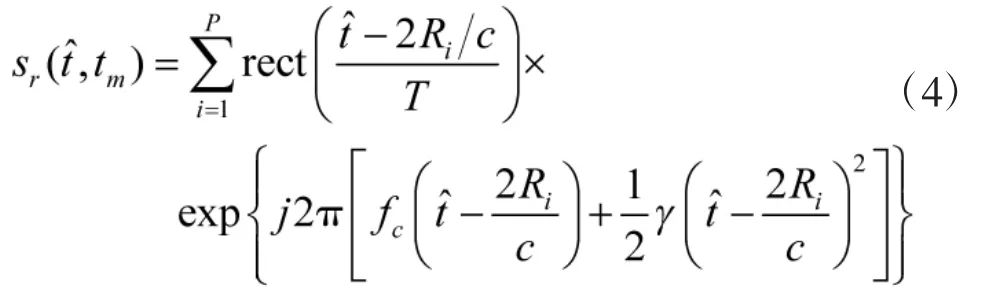
式中：P为目标散射点的个数。

目标第i个散射点到雷达的距离可以表示为：

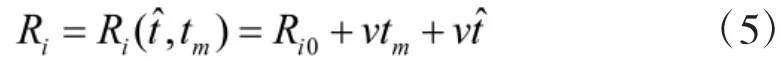
式中：Ri0是第i个散射点相对雷达的初始距离，v为目标距离向速度。

目标回波经过混频后得到信号：

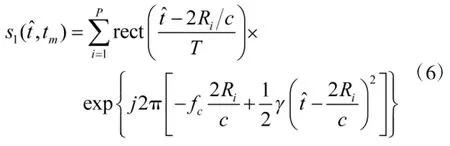
将式（5）代入式（6），同时注意到对于某次回波脉冲而言，脉间距离走动Rim=Ri0+vtm为常数，将式（6）展开得到：

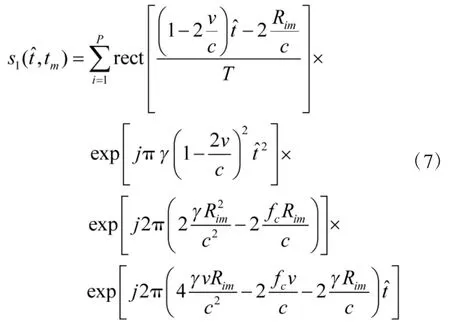
从式（7）可以看出，该信号是一个二次相位信号。其中的第2个相位项与Rim和v两个未知参数有关，第3个相位项只与参数v有关。该信号对于匀速目标而言，是具有固定调频率和多个载波频率的多分量线性调频信号。

将该信号进行调频傅里叶变换：

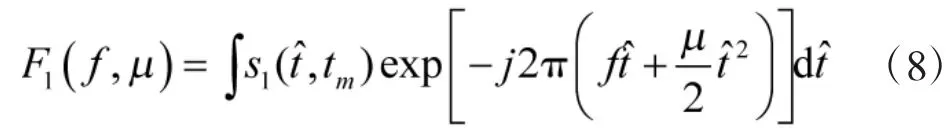
经过式（8）可以得到调频傅里叶变换谱图，搜索峰值可以得到v和Rim的估计值v~和R~im。注意到由于噪声的干扰，参数估计会产生误差。根据目标速度的相对稳定性，对于速度v的估计，可以利用相邻几个脉冲的估计值求平均来部分抵消噪声的干扰，提高估计的精度。在估计出速度v后，也可以根据速度、脉冲重复周期和距离Rim的关系，利用相邻几个脉冲求取距离Rim平均值的，部分抵消噪声对于距离参数的干扰。

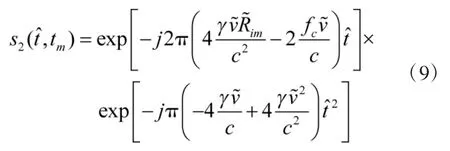
应用该相位补偿信号对式（7）进行逐次回波补偿，得到初步消除脉内走动后的信号：

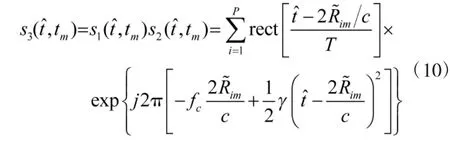
为了进一步消除脉内走动，可以对式（10）进行调频傅里叶变换，得到距离像，从距离像的走动轨迹中精确估计速度，再次回波补偿脉内走动。式（10）可以化为以下表达式：

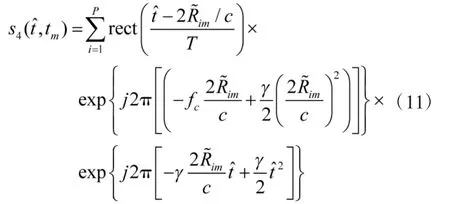
可以看出该信号为二次相位信号，且其调频率是已知的，载波频率项未知，且仅与距离相关。对于单次回波来说，不考虑脉内走动，则是常数，所以对式（11）进行逐次回波的调频傅里叶变换，得到的一维谱图仅与目标散射点的位置有关，即类似于脉冲压缩得到的一维距离像。

对式（11）进行一维调频傅里叶变换：

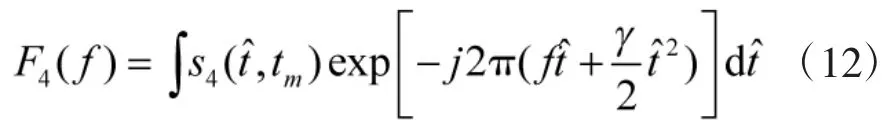
式中：调频傅里叶变换核的调频率为γ，载波频率为f。

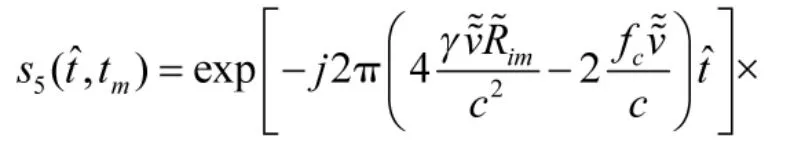
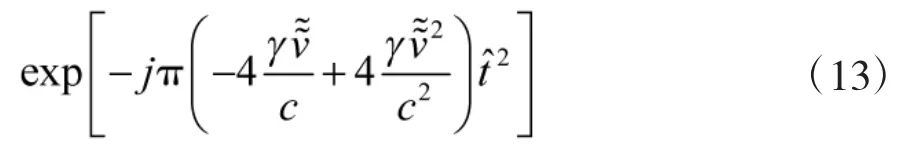
至此就完成了脉内速度精确补偿。脉内速度补偿后的信号只需考虑脉间距离走动，此时就可以应用传统的包络对齐来消除脉间距离走动，得到目标的距离像。

本算法的原理框图如图1所示。

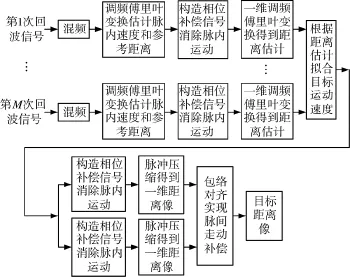
图1 算法原理框图

1.3算法复杂度及其对ISAR成像的影响

1.3.1算法复杂度分析

对于本算法的主体结构调频傅里叶变换，用到了二维调频傅里叶变换和一维调频傅里叶变换两种，即图1中的“调频傅里叶变换估计脉内速度和参考距离”、“一维调频傅里叶变换得到距离估计”两个步骤。根据式（8），如果信号采样点数为N点，那么对于一个P×Q维调频傅里叶变换的计算量近似为P×Q×N次复数乘法，所以必须尽可能减少参数搜索点数。

由式（7）可以看出，调频傅里叶变换的两个估计参数（f，μ）实际上对应（v，Rim），所以搜索区间根据速度和距离信息进行设置。为了减少参数二维搜索的计算量，可以充分利用速度和距离的先验知识设置合理的搜索区间，并采用由粗到精的搜索方法。

在信噪比不是很低的情况下，可采用如下的循环搜索方法：先固定距离值，以较大间隔搜索速度，然后固定速度值，以较大间隔搜索距离，以此循环，最终以精细的间隔搜索得到距离和速度值。例如：为了实现一个距离范围1000m、速度范围1000m/s区间，精度达到距离1 m、速度1 m/s的搜索，如果直接在整个搜索范围内搜索，则大致需要1 000×1 000×N次复数乘法。如果采用循环搜索方法，首先固定一个距离值，然后以100 m/s为间隔得到速度估计，然后固定速度值，以100 m为间隔得到距离的估计，以此类推，每次下降一个数量级，进行6×10×N次复数乘法就可以得到相同精度的搜索结果，计算量大大降低。可以看出，通过循环搜索方法，二维调频傅里叶变换的计算量实际和二维参数的搜索区间有关，搜索区间越小，计算量越小。所以对于ISAR雷达实际成像而言，初始脉冲需进行较大范围的搜索，一旦搜索出目标运动参数，后续的脉冲搜索范围将有很强的针对性，搜索量将会大大减少。

对于式（7）所示的多分量线性调频信号参数估计，分数阶傅里叶变换（FRFT）和本文的调频傅里叶变换一样是一种线性变换，不存在双线性时频分析方法的交叉项问题，且计算量也比双线性视频分析方法低。以下对比本文算法和FRFT算法的计算量。

对于FRFT，其参数搜索的运算量为O［AN log2N］［4-5］，其中N为信号向量采样点数，A取决于变换阶数的离散一维搜索量。如果N取1 024，A取100，则计算量约为10×100×1 024次复数乘法。这个运算量相当于一个10×100维的二维调频傅里叶变换的运算量，而比采用上述循环搜索的调频傅里叶变换运算量要大很多。所以，本文的算法计算量相对别的算法要低，具有明显的优势。

1.3.2算法对ISAR成像的影响

图1的算法原理框图可以分为3步，以下分别分析每个部分对ISAR整体成像时间的影响：

①算法第1步进行的脉内运动初步补偿，具体讲是由“混频”至“一维调频傅里叶变换得到距离估计”4个步骤实现的。该过程是在每个回波到来时进行的，运算的主体是在脉冲间隙内实现，所以不占用成像整体时间。

②算法第2步进行的是脉内运动精确补偿得到目标距离像，这个步骤是由“根据距离估计拟合目标运动速度”、“构造相位补偿信号消除脉内运动”、“脉冲压缩得到一维距离像”3个步骤实现，这3个步骤是在所有回波到来之后进行处理的，所以需占用整体成像时间。

③算法的第3个步骤是包络对齐得到目标距离像，和基础的ISAR成像算法一致。

根据以上分析，本文算法比基础的ISAR成像算法：脉冲压缩、包络对齐、相位聚焦、方位向FFT，在整体成像时间上增加了“根据距离估计拟合目标运动速度”、“构造相位补偿信号消除脉内运动”、“脉冲压缩得到一维距离像”3个步骤的处理时间。但由于这3个步骤计算很简单，所以对整体成像时间而言只产生很小的额外时间开销。

2 仿真试验

线性调频信号的仿真参数如下：载波频率F0= 5 GHz，带宽B=1 GHz，脉冲持续时间T1=100 μs，调频率γ=B/T1，脉冲周期Tp=10 ms。

实验1单点目标消除脉内走动

设定目标的参考点初始距离R0=50 km，散射点距离向坐标x=10 m，方位向坐标y=0，目标速度v=5 000 m/s，目标运动方向指向雷达。图2显示了未进行脉内速度补偿的单个脉冲距离压缩结果，图像幅度进行了归一化。可以看出该距离像的位置发生了移动，由10 m处移动到9.2 m处，而且sinc函数峰产生展宽与分裂。对式（7）进行调频傅里叶变换，可以观察到f-μ的参数估计情况。图3（a）显示了距离估计结果（该图已将参数f换算为距离），峰值R~im位于9.2 m处，可以看出该估计和脉冲压缩结果一致。图3（b）显示了调频率估计结果，其峰值μ~位于1.000 067×1013处，根据式（7）的对应关系，可以求得速度的估计值为5 025 m/s，可见速度估计精度较高。按照式（9）构造出相位补偿函数和式（7）相乘，可以初步抵消目标脉内运动。下页图4显示了初步抵消目标脉内运动后的脉冲压缩结果和理想脉冲压缩之间的比较，从图中可以看出消除脉内走动后的结果是很精确的。

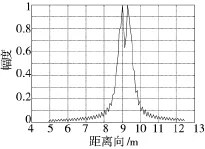
图2 未进行脉内速度补偿的脉冲压缩结果

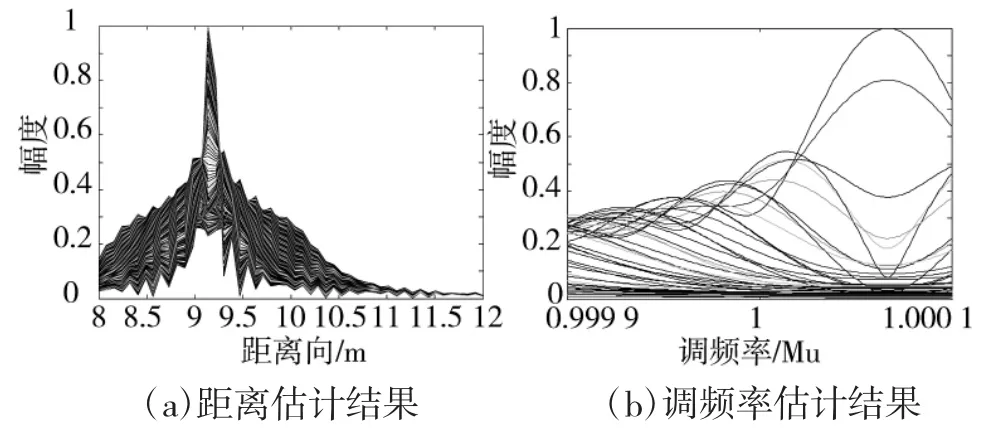
图3 调频傅里叶变换结果

实验2脉内速度补偿的目标距离像

9个散射点距离向坐标x=［8，8.5，9，9.5，10，10.5，11，11.5，12］，方位向坐标均为y=0，其他参数不变，通过100个回波脉冲进行仿真。

图5（a）显示了未经脉内速度补偿的脉冲压缩一维距离像，由于速度引起脉冲压缩sinc函数峰值分裂，该图无法分辨真实的散射点。图5（b）为通过总体相关法得到的包络对齐后的距离像，该距离像只显示了前10个脉冲。图6为混频后的回波信号经过调频傅里叶变换得到的目标距离估计，此时由于没有消除脉内走动，目标位置和实际位置存在偏离。对比图5（a）和图6可以看到脉冲压缩的散射点sinc函数图像分裂的情况得到了很大改善。图7（a）是通过速度估计构造相位补偿函数得到的消除脉内走动后的脉冲压缩一维距离像，从该图可以看出一维距离像已经很理想。图7（b）是前10个脉冲的距离像，比较图5和图7可以看出距离像得到了较理想的补偿。

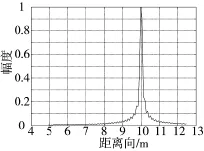
图4 脉内速度补偿后的脉冲压缩结果

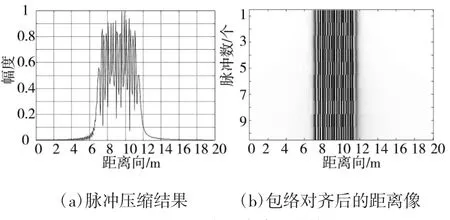
图5 未经补偿的脉冲压缩结果

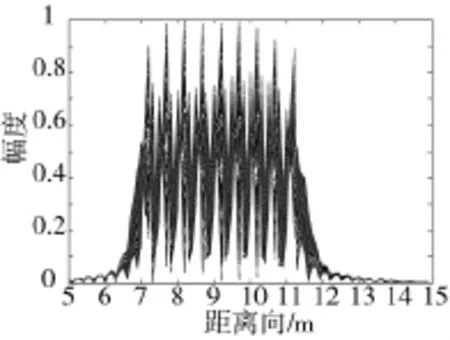
图6 调频傅里叶变换的距离估计

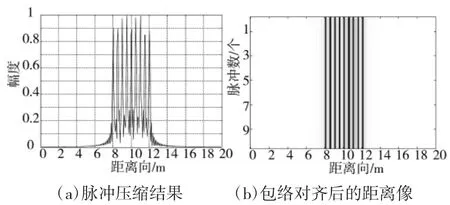
图7 速度补偿后的脉冲压缩结果

3 结论

调频傅里叶变换是一种线性变换，对线性调频信号的处理有先天的优势。本文采用调频傅里叶变换对线性调频体制雷达的回波信号进行参考距离、速度的估计，可以精确补偿高速目标引起的脉内走动，从而得到目标的距离像。本算法的主体算法在脉冲重复周期内进行，可以满足实时成像和参数估计的需求。

［1］邢孟道，保铮，郑义明.用整体最优准则实现ISAR成像的包络对齐［J］.电子学报，2001，29（12A）：1808-1811.

［2］杨小优，池龙，何劲，等.一种逆合成孔径激光雷达成像算法［J］.激光与红外，2010，40（8）：904-909.

［3］张焕颖，张守宏，李强.高速运动目标的ISAR成像方法［J］.电子与信息学报，2007，29（8）：1789-1793.

［4］战立晓，汤子跃，朱振波.基于分数阶傅里叶变换的加速微弱目标检测与估计［J］.电波科学学报，2013，28（2）：296-304.

［5］阮航，吴彦鸿，叶伟.基于FRFT-CLEAN的机动目标逆合成孔径激光雷达成像算法［J］.电子与信息学报，2013，35（7）：1540-1546.

［6］付耀文，胡杰民，黎湘.基于调频傅里叶变换的匀加速转动目标ISAR成像［J］.系统工程与电子技术，2011，33（12）：2608-2612.

［7］王盛利，李士国，倪晋麟，等.一种新的变换--匹配傅里叶变换［J］.电子学报，2001，29（3）：403-405.

ISAR Range Imaging Method of High-Speed Targets Based on Chirp-Fourier Transform

LUO Wen-mao1，CUI Ying-liu2
（1.Department of Telecommunication，Nanjing College of Information Technology，Nanjing 210023，China；2.School of Technology，Nanjing Audit University，Nanjing 211815，China）

In the high resolution radar system with large time-bandwidth LFM signal，the high speed of target will cause serious Doppler dispersion.In order to get correct imaging result，the Doppler dispersion must be eliminated.A novel range imaging method based on the chirp-Fourier transform is proposed，which can estimate the motion parameters of intra-pulse and compensate the intra-pulse motion to get the correct range profile.The method firstly estimates the intra-pulse motion parameters and preliminary compensate the motion，and then estimates the motion trajectory to further compensate the motion.After the intra-pulse compensation it can get the correct range profile by envelope alignment.The main parts of the algorithm are handled in the pulse repetition period，so it can meet the demand of real-time imaging and parameter estimation.

ISAR，chirp-Fouriertransform，LFM，high-speedmovingtarget，intra-pulsecompensation

TN97

A

1002-0640（2016）11-0036-05

2015-10-20

2015-11-17

国家自然科学基金（61170105）；江苏省高职院校高级访问学者资助项目；南京信息职业技术学院“青蓝工程”基金资助项目

罗文茂（1975-），男，四川乐山人，硕士，副教授。研究方向：雷达信号处理。