出动强度约束下多机种(型)保障资源优化配置

杨甫勤,夏军剑，路学成

(1.军事交通学院 军事物流系，天津 300161； 2.军事交通学院 基础部，天津 300161)



出动强度约束下多机种(型)保障资源优化配置

杨甫勤1,夏军剑2，路学成1

(1.军事交通学院 军事物流系，天津 300161； 2.军事交通学院 基础部，天津 300161)

在多机种协同作战中，场站保障资源配置对飞机的出动强度具有重要影响。在运用多类顾客多服务器的排队网络模型描述飞机多机种(型)出动回收过程的基础上，结合多类顾客平均值分析，建立场站保障资源边际优化模型并给出算法求解流程。通过解析计算，给出飞机多机种(型)出动强度和保障资源优化过程曲线以及出动强度与保障资源总费用间关系曲线，揭示出动强度随迭代次数及资源总费用的变化规律；最后将资源优化配置结果与经验配置进行比较。结果表明，与传统的经验配置相比，该模型在满足出动强度目标的前提下，能较好地降低资源总费用，有效提高保障资源配置水平。

系统工程；资源优化配置；边际分析；多机种；排队网络

场站保障资源优化配置问题属于离散事件动态系统的资源配置优化问题，目前，解决该问题的主要方法是仿真。Faas[1]采用离散事件仿真工具分别构建了两种保障系统的飞机出动架次过程模型，研究表明自治后勤系统可以缩短维修保障过程，提高飞机的出动能力。Mackenzie等[2]建立了基于智能体的飞机出动过程模型，重点研究了维修组织中各种维修资源效率对飞机出动强度的影响。Feng等[3]采用多智能体技术建立了飞行保障过程中面向任务的飞机维修资源调配优化模型，并采用CNP配置算法进行求解，讨论维修资源的最优配置及其相互关系对资源配置的影响。Norin等[4]建立了飞机在此出动过程中机场地面保障车辆优化仿真模型，结果表明优化保障资源可以减少延误和等待时间。夏国清等[5]针对单个机种保障过程，建立面向出动强度的飞机出动过程排队模型，综合考虑资源数量和资源费用的影响。

然而，上述文献均没有研究多个机种(型)同场次出动时保障资源优化配置问题。本文考虑综合保障场站实施多机种保障的实际情况，运用多类顾客多服务器的排队网络模型描述飞机多机种(型)出动回收过程，建立场站保障资源边际优化模型，结合边际分析法和平均值分析对优化模型进行求解。优化保障资源配置，综合考虑保障资源的数量和费用对出动能力的影响，在满足设定出动强度目标约束的前提下，得到多机种(型)出动过程保障资源的最优配置。

1 飞机多机种(型)出动保障过程排队网络模型

在空军综合场站的多机种保障任务中，由于飞机种类、执行任务类型等因素的不同，所需要的保障装备、保障时间、保障过程可能有所不同，但无论是歼击机、强击机，还是轰炸机等军用飞机，从降落到再次出动执行任务，地面保障人员通常要对其进行检测、维修或维护、加油、挂弹等一系列保障活动。根据排队理论，可以将多机种看作多个类型的顾客，各项保障活动看作多类顾客到达各服务中心接受相应服务，飞机无转场或损毁，多机种出动回收过程就形成一个含有R类顾客和M个服务中心的封闭系统，可以采用多类顾客多服务器闭排队网络对其进行建模和分析(如图1所示)。某机种(型)飞机在服务中心i接收保障服务后，以一定概率pij在各服务中心间转移，整个出动回收过程中的转移概率可用转移概率矩阵P=[pij]M×M表示。

由图1可知，可将飞机在机场降落看作飞机出动回收过程的起点，飞机飞行中如出现故障，就以概率p12转移到检测服务中心2进行故障检测，完成故障分析，确定维修方案后以概率p23转移到维修服务中心3进行故障维修后，以概率p34转移到维护服务中心4接受维护服务。如飞行中没有出现故障，则以概率p14直接转移到维护服务中心4进行例行维护。飞机完成维护保障活动后，以概率p45转移到管道加油服务中心5或者以概率p46转移到油车加油服务中心6进行加油。最后飞机以概率p67转移到挂弹服务中心7进行挂弹保障。完成各项保障活动后飞机升空执行任务，结束任务后飞机降落，开始下一次的循环。

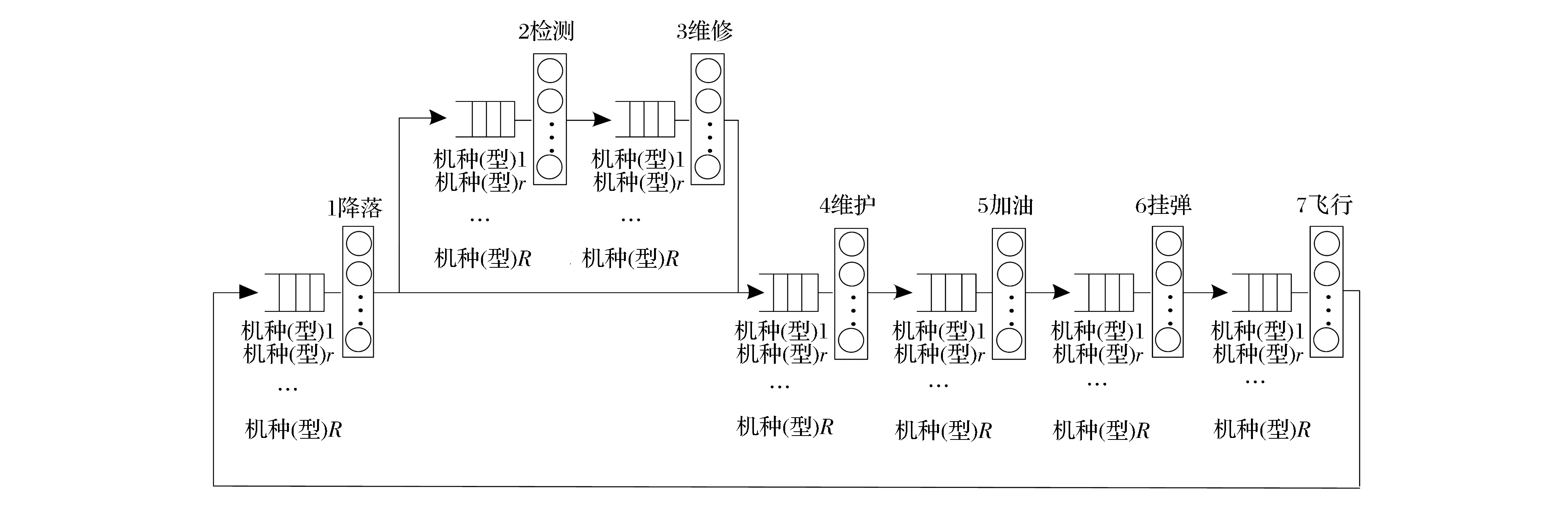
图1 多机种(型)飞机出动回收过程

2 飞机多机种(型)出动保障资源优化配置模型

2.1 飞机多机种(型)出动强度计算

飞机出动强度指单位时间内飞机能够连续出动的次数。在上述飞机多机种(型)出动回收过程中，飞机在飞行服务中心8的吞吐量就是该种(型)飞机的出动强度，可以采用平均值分析对其进行求解。为便于进行模型求解，对该模型假设如下。

假设1：多机种(型)排队网络中含有R种(型)飞机和M个服务节点，各类飞机数量用向量k=(k1，k2，…,kr)表示，其中kr为网络中第r种(型)飞机的数量。

假设2：同一服务中心的服务器对同一种飞机服务能力相同且服务时间服从均值为Sir的负指数分布。如果服务中心i的服务器数量为有限个mi，则各类飞机按照先到先服务的排队规则在任一服务器接受服务；如果服务中心i的服务器数量为无限个，则各类飞机无需排队，立刻在任一服务器接受服务。

假设3：各服务中心的飞机排队数量无限制。

根据平均值分析法，第r种飞机在有限个服务窗mi的服务中心i的平均逗留时间为

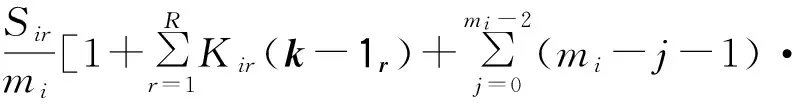
Pi(j|(k-1r))]

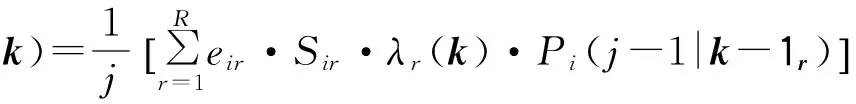
式中：eir为第r种(型)飞机对第i服务节点的访问率；λr(k)为第r种型飞机的吞吐量。

若j=0，则Pi(0|k)为

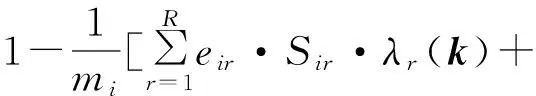
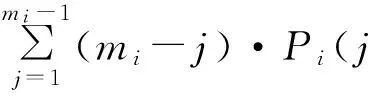
如果第r种飞机到达具有无限个服务器的服务中心i，则因飞机不需等待，其平均逗留时间Rir(k)简化为

Rir(k)=Sir

根据Little′s公式，第r种(型)飞机服务节点i的吞吐量为

同理，第r种(型)飞机在第i服务节点的平均队长Qir(k)为

Qir(k)=λir(k)·Rir(k)

根据上述方程组，设定排队网络初始状态Qir(0)=0，Pi(0|0)=1，Pi(j|0)=0，就可以逐步迭代出网络状态为k时，各种(型)飞机在各个服务节点的平均逗留时间Rir(k)、吞吐量λir(k)、平均队长Qir(k)等性能指标。即可以计算出一定资源配置下各类飞机的出动强度，以及找出约束飞机出动能力的瓶颈环节，但是，该方法不能根据出动强度的需要，给出各类保障资源的最优配置方案。本文在上述算法的基础上，建立资源配置边际优化模型，对多机种(型)保障资源配置进行优化。

2.2 保障资源配置边际优化模型

在飞机多机种(型)出动保障过程排队网络中，除飞机在空中执行任务外，各种(型)飞机所需要的场站保障资源包括跑道、检测、维修、维护、挂弹装备以及加油管道或加油车辆等。其中，除跑道数量m1在场站建设完成即确定，受到数量调配约束外，其他保障资源数量均可根据需要进行调配。因此，保障资源配置边际优化模型应为在满足各机种(型)出动强度目标和跑道数量约束等指标的前提下，多机种(型)出动过程中各类保障资源的总费用最低，即

式中：C为场站各类保障资源的总费用；cir为服务中心i保障第r种(型)飞机的单个保障资源的费用系数，是一个相对值；λtr为第r种(型)飞机的目标出动强度；m0为场站跑道数量。其中，各项保障资源的边际效益δ(mi)为

式中λ8r(mi+1)-λ8r(mi)为由于在服务中心i增加1个服务器而产生的第r种(型)飞机的吞吐量增量。

2.3 保障资源配置边际优化模型求解算法

边际优化模型求解方法是一种迭代算法，是在确定系统可变资源的前提下，在每次迭代中将可变资源数量依次增加1个单位，计算并比较由各资源增量所产生的目标增量，选取最大的目标增量对应的资源并将其数量增加一个单位，作为下次迭代的初始值，如此反复迭代直至达到所设定的目标值。

3 算例分析

以空军某场站同场次出动两种飞机为例，已知该场站有两条跑道，由演习计划得知，两种飞机各48架，组成混编机群出动，要求连续作战中两种飞机的出动强度分别达到15架/h和12架/h，假设各服务中心的保障设备(服务器)均为通用设备，飞行服务中心不占用场站保障资源。根据图1所示飞机出动回收过程，两种飞机分别在各服务中心的服务时间(服从负指数分布)、各服务中心配置服务器数量及其费用系数见表1。

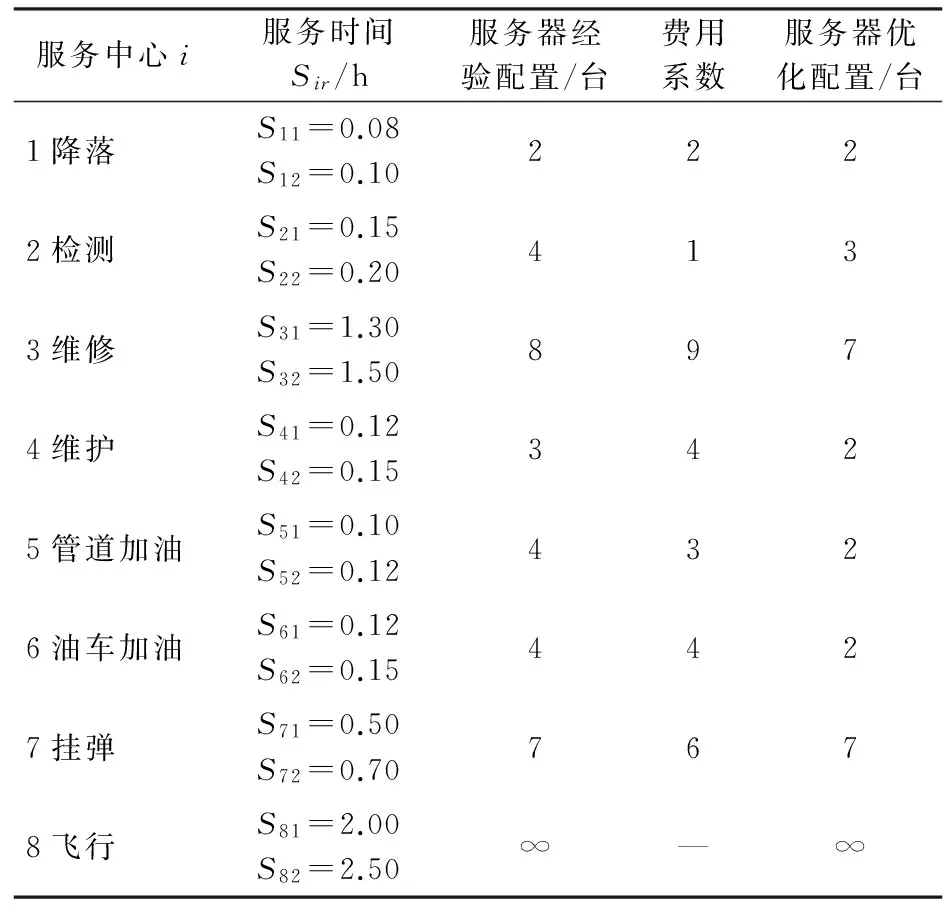
表1 多机种(型)飞机出动回收过程相关参数

假设各类飞机出动过程中路由转移矩阵相同，均为

根据表1中参数，使用2.3提出的边际优化模型及算法流程，运用Matlab进行编程，在第19次迭代过程中，在满足跑道数量约束条件的前提下，两种飞机的出动强度分别为15.05架/h和12.24架/h，均达到设定的目标值，得到各服务中心的服务器最优配置(见表1)。在迭代优化过程中，随着迭代次数的增加，各服务中心的服务器数量不断调整，两种飞机的出动强度不断接近并最终达到目标值，其变化曲线如图2、图3所示。

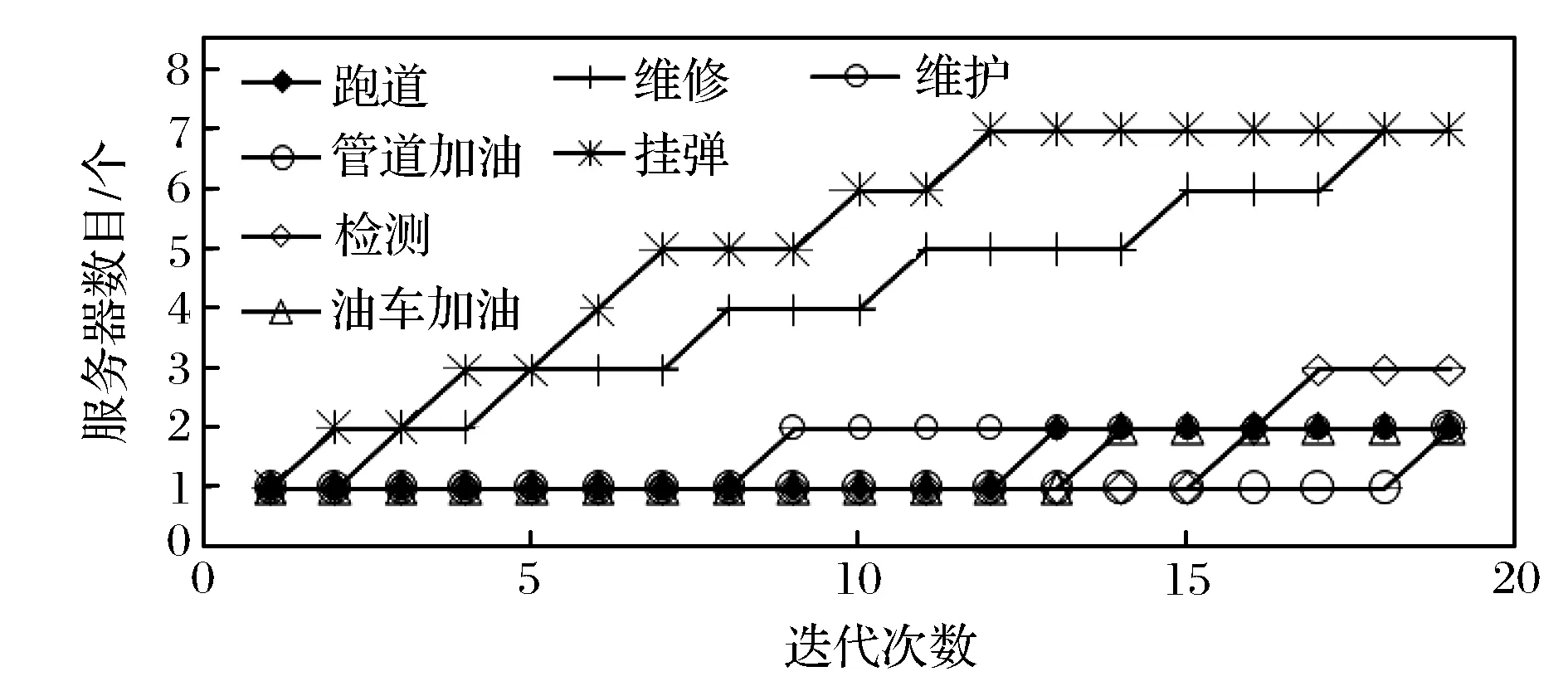
图2 各服务中心服务器数量迭代过程

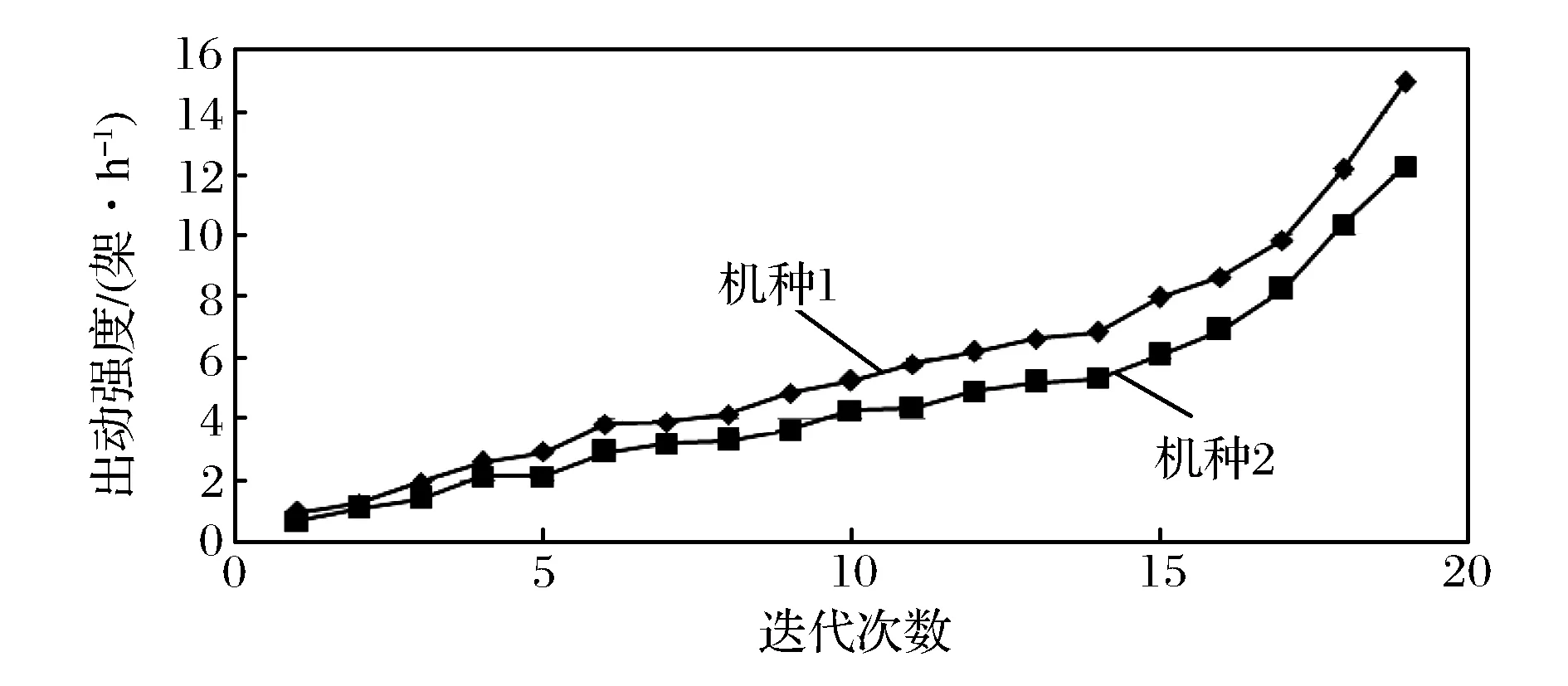
图3 各种(型)飞机出动强度迭代过程

由图2和图3可知:两种飞机的出动强度曲线随迭代次数的增加而增加，其增加幅度先缓后急，表明出动强度在迭代起始阶段增加缓慢，所受资源数量限制较多，主要是受到维修和挂弹保障资源的限制；在经过15次迭代后，出动强度均以较快速度增加，并达到目标值，表明各服务中心的服务器数量逐步趋于合理，资源配置得到优化。

图4显示了各种(型)飞机出动强度随各服务中心的资源总费用的增加而增加的关系曲线。

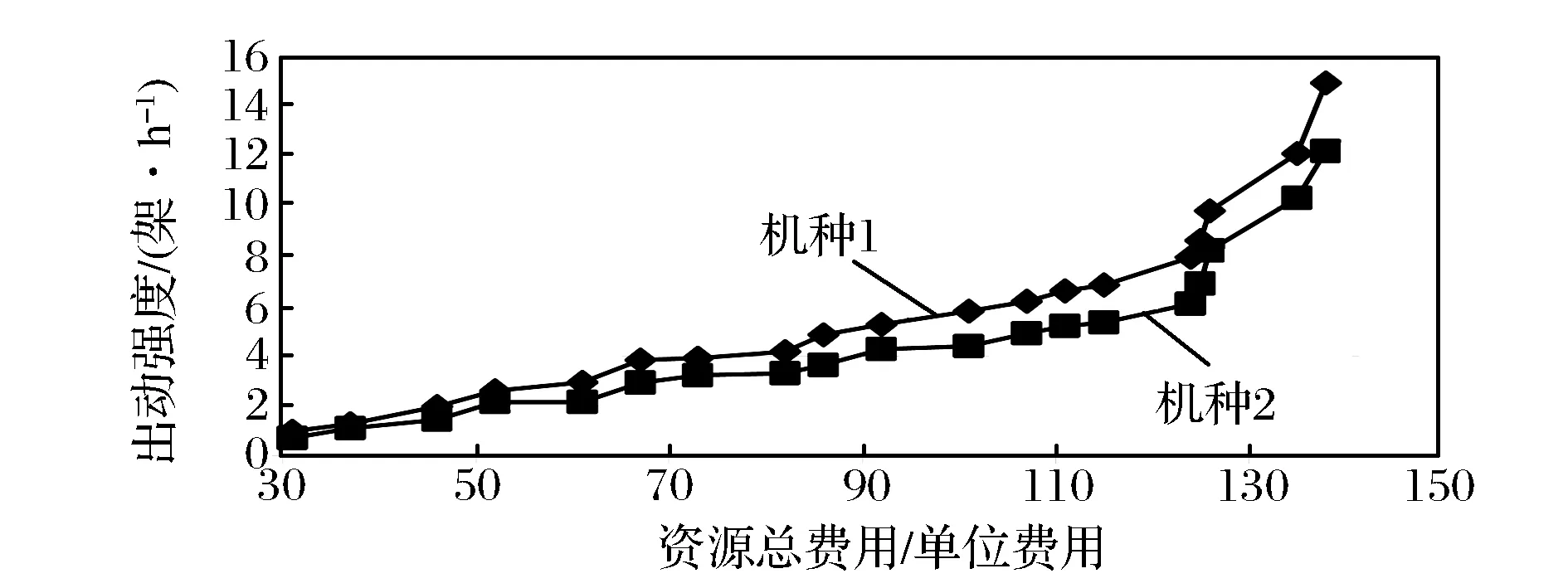
图4 各种(型)飞机出动强度与资源总费用间关系曲线

飞机出动强度的增加也是先缓后急，在起始阶段，出动强度随保障资源总费用的增加平缓增加，经历一定阶段后，在资源总费用平缓增长的情况下，出动强度快速增长，进一步表明该阶段各种资源匹配合理，资源配置趋于优化。在两种飞机分别达到出动强度目标的前提下，优化后的资源配置总费用为134，比以往的经验配置资源总费用(由表1计算可得 162)减少了17.28%，表明该方法具有较好的优化效果。

4 结 语

本文针对飞机多机种(型)同场次出动时保障资源优化配置问题，提出了一种基于多类顾客多服务器的排队网络模型，该模型运用边际分析法和平均值分析，对多机种(型)出动过程中的资源配置进行求解，分别讨论出动强度与保障资源数量和保障资源总费用之间的关系。可以看出，与传统的经验配置相比，该模型在满足出动强度目标的前提下，能较好地降低资源总费用。研究结果表明，采用科学的资源配置量化方法，能有效提高保障资源配置水平，从而提高保障系统的军事效益和保障经费的经济效益。

[1] FAAS D P.Simulation of autonomic logistics system sortie generation[M].New York:Biblioscholar,2012：61-99.

[2] MACKENZIE A,MILLER O J,HILL R R,et al.Application of agent based modelling to aircraft maintenance manning and sortie generation[J]. Simulation Modelling Practice & Theory，2012，20(1): 89-98.

[3] FENG Q, LI S J,SUN B.A multi-agent based intelligent configuration methodfor aircraft fleet maintenance personnel[J]. Chinese Journal of Aeronautics, 2014, 27(2):280-290.

[4] NORIN A,GRANBERG A T,YUAN D,et al.Airport logistic:a case study of the turn-around process[J]. Journal of Air Transport Management,2012，20(3):31-34.

[5] 夏国清，陈红召，米青超.面向架次率的机场资源配置优化模型[J]. 火力与指挥控制, 2013，38(6)：139-142.

(编辑：史海英)

Resources Optimal Allocation of Multi-aircraft Support Under Constraint of Sortie Rate

YANG Fuqin1, XIA Junjian2, LU Xuecheng1

(1.Military Logistics Department, Military Transportation University, Tianjin 300161, China；2.General Courses Department, Military Transportation University, Tianjin 300161, China)

Resources allocation has great significance for aircraft sortie rate in multi-aircraft cooperative combat. The paper establishes marginal optimization model and shows solving procedure combining with multi-customer average value on the base of applying multi-customer multi-server queuing network model in multi-aircraft sortie process. It shows the curve of multi-aircraft sortie rate and resources optimizing process and the relation curve between sortie rate and support resource expense after analyzing and calculating, and reveals the rule of sortie rate changing with iterations and sources expense. It also compares resources optimal allocation result with that of experienced allocation. The result shows that this model can better reduce resources expense and improve support resources allocation level on the premise of satisfying sortie rate.

systems engineering; resource optimal allocation; marginal analysis; multi-aircraft; queuing network

2016-01-02；

2016-04-19．

军事后勤科研项目(12KZ3G1-010KC)．

杨甫勤(1976—)，女，博士，讲师．

10．16807/j.cnki.12-1372/e.2016.11.014

TP301.6

A

1674-2192(2016)11- 0059- 04