基于Profili软件的风力机叶片表面雷诺数分析
2016-12-08曹利刚郭改琴
曹利刚,郭改琴
(杨凌职业技术学院 机电工程学院,陕西 杨凌 712100)
基于Profili软件的风力机叶片表面雷诺数分析
曹利刚,郭改琴
(杨凌职业技术学院 机电工程学院,陕西 杨凌 712100)
通过计算不同的风力机安装高度、叶片的弦长和平均风速时的雷诺数,分析研究得到雷诺数的变化规律,从而间接反应流体的流态,这为设计风机提供了重要的理论依据.
安装高度;弦长;风速;雷诺数
在流体运动中惯性力和黏性力的比值影响着雷诺数,根据雷诺数的大小可以将流体分为层流和湍流两种流场[1]61,[2] 11-12.不同的流场叶片的气动性能不相同,风力机的效率就不相同,所以在风力机设计时就要充分考虑到雷诺数.Profili是一款翼型的专业设计软件[3]40-41,可以计算出不同的高度、不同的弦长及不同风速时的雷诺数.所以找出风机的安装高度、叶片的弦长和风速对雷诺数的影响规律,就能为设计风机提供重要的理论参考依据.
1 影响雷诺数的因素分析
风力发电机的容量不同,叶片的长度也就不同,因此安装风力机叶片的塔架高度也就不同[4]14-15,[5]129,一般情况下高度有几米、几十米,有的甚至达到一百多米.风力机叶片的弦长是决定风机容量的重要因素之一,其长度一般在几十厘米到六七米之间.平均风速也是影响风机效率的重要因素,其数值一般在1 m/s至20 m/s之间.风机安装高度、叶片弦长和平均风速共同影响着雷诺数的大小,通过固定两个参数让第三个参数由小到大有规律的变化,就可以通过Profili软件计算出相应的雷诺数[6]29-30,[7]24-25,再通过对计算数值分析研究就可得到雷诺数的变化规律.
2 高度对雷诺数的影响
假设风速为15 m/s,弦长为300 cm这两个参数不发生变化,叶片的安装高度从5 m到100 m每隔5 m为一个高度,共计20个不同高度.计算的雷诺数及其增长率如表1所示.

表1 不同高度时的雷诺数及增长率
分析表1中高度、雷诺数和增长率的相关数据后可得如图1所示的结果,容易得到当风速和弦长不变时,随着高度的等量递增,相应的雷诺数连成了一条水平直线,可见其数值几乎没有发生变化;雷诺数的增长率也连成了一条水平直线,也没有发生变化,说明同一高度的流体状态基本相同.通过多次改变假设条件中的风速和弦长的数值,当高度递增变化时得到同样的结果,所以这充分说明当平均风速和叶片的弦长不变时,风机的安装高度不同,但雷诺数基本相同,也就是流体的流态基本相同.
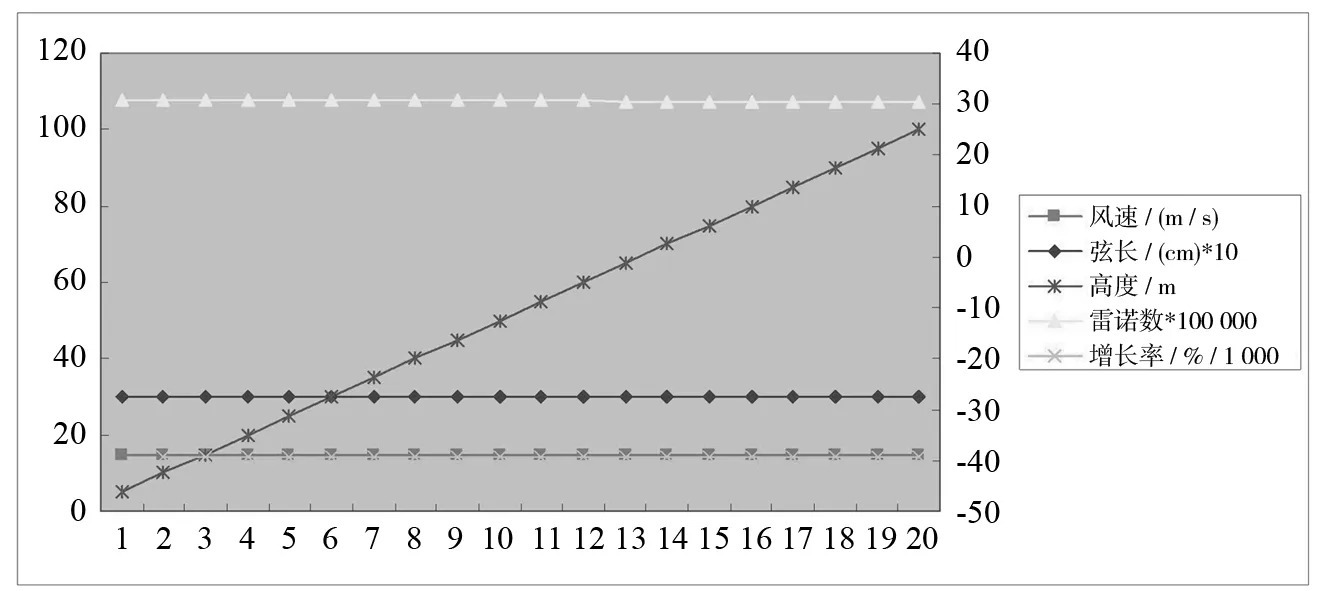
图1 不同高度时雷诺数及其增长率数据分析
3 风速对雷诺数的影响
假设叶片的安装高度为50 m不变,叶片的弦长为300 cm不变,平均风速从1 m/s到20 m/s每隔1 m/s变化1个风速,共计20个不同风速.计算的雷诺数及其增长率如表2所示.

表2 不同风速时的雷诺数及增长率
分析表2中风速、雷诺数和增长率的相关数据后可得如图2所示的结果,容易得到当高度50 m和弦长300 cm不变时,随着风速的等量递增其相应的雷诺数也呈现出等量递增的变化趋势,并与风速的变化曲线几乎重合;雷诺数的增长率呈现出一条曲线的变化趋势,由风速为3 m/s的50%迅速递减到风速为5 m/s的25%,随后递减速度迅速减弱,最后达到20 m/s的5%.通过多次改变假设条件中的安装高度和弦长的数值,当平均风速递增变化时得到同样的结果,所以这充分说明当风机安装高度和叶片的弦长不变时,随着平均风速的变化,其对应的雷诺数也在发生相同规律的变化,所以流体的流态也就发生了变化,但是随着风速的增加雷诺数的增长率在不断减小,说明随着风速的增加,当达到10 m/s时流态基本趋于稳定.

图2 不同风速时雷诺数及其增长率数据分析
4 弦长对雷诺数的影响
假设叶片的安装高度为50 m不变,平均风速15 m/s不变,叶片的弦长从30 cm到540 cm每个30 cm变化1个数值,共计18个不同的叶片弦长.计算的雷诺数及其增长率如表3所示.

表3 不同弦长时的雷诺数及增长率
分析表3中弦长、雷诺数和增长率的相关数据后可得如图3所示的结果,容易得到当高度50 m和平均风速为15 m/s不变时,随着弦长的等量递增其相应的雷诺数也呈现出等量递增的变化趋势,但变化曲线的斜率明显要小于弦长变化曲线的斜率;雷诺数的增长率呈现出一条曲线的变化趋势,由弦长为90 cm的50%迅速递减到弦长为180 cm的20%,随后递减速度迅速减弱,最后达到弦长为540 cm的6%.通过多次改变假设条件中的安装高度和平均风速的数值,当叶片弦长递增变化时得到同样的结果,所以这充分说明当风机安装高度和平均风速不变时,随着叶片的弦长不断增加,其对应的雷诺数也在增加,所以流体的流态也在不断地发生变化;但是随着弦长的增加雷诺数的增长率在不断减小,当弦长达到330 cm后,流态基本趋于稳定.
5 结语
当平均风速和叶片的弦长不变而高度变化时,对应的雷诺数基本相同,这就说明流体的流态基本趋于稳定;当风机的安装高度和叶片的弦长不变时,随着平均风速的变化,雷诺数也发生着与风速相同的变化规律,伴随着流体的流态也就发生了变化,当风速达到10 m/s时流态基本趋于稳定;当风机安装高度和平均风速不变时,随着叶片的弦长不断增加,其对应的雷诺数也在增加,伴随着流体的流态也在发生着变化,弦长达到330 cm后,流态基本趋于稳定.
[1] 闵新勇.风力机翼型的气动性能模拟与优化设计[D].上海:上海交通大学,2010.
[2] 李海峰.风力机专用翼型及其设计分析方法研究[D].重庆:重庆大学,2010.
[3] 尹耀安.大型风力机叶片设计与CFD分析[D].武汉:华中科技大学,2008.
[4] 赵丹平.风力发电机组叶片模型气动载荷研究[D].呼和浩特:内蒙古工业大学,2009.
[5] 冀润景.风力机叶片设计方法的发展[J].中国电力教育,2006(S1).
[6] 吴金明.水平轴马格努斯风力机叶片的气动性能研究[D].哈尔滨:哈尔滨工业大学,2012.
[7] 沈坤荣.大型水平轴风力发电机组叶片空气动力学设计[D].上海:上海交通大学,2012.
[责任编辑 梧桐雨]
2016-05-30
杨凌职业技术学院科学研究基金项目(项目编号:2014009A)
曹利刚(1980- ),男,陕西澄城人,杨凌职业技术学院讲师,主要从事水电站自动化及流体机械研究。
1671-8127(2016)05-0075-03
TK83
A
