匿名CLPKC-TPKI异构签密方案

张玉磊，张灵刚，张永洁，王 欢，王彩芬

(1.西北师范大学计算机科学与工程学院，甘肃兰州 730070； 2.甘肃卫生职业学院，甘肃兰州 730000)



匿名CLPKC-TPKI异构签密方案

张玉磊1，张灵刚1，张永洁2，王 欢1，王彩芬1

(1.西北师范大学计算机科学与工程学院，甘肃兰州 730070； 2.甘肃卫生职业学院，甘肃兰州 730000)

异构签密可以保证不同公钥密码系统之间数据传输的机密性和不可伪造性.本文定义了从无证书公钥密码环境到传统公钥密码环境(CLPKC→TPKI)异构签密方案的形式化模型，并利用双线性对提出了一个CLPKC→TPKI异构签密方案.在随机预言模型下，基于计算Diffie-Hellman和修改逆计算Diffie-Hellman困难假设，证明方案满足内部安全的机密性和不可伪造性.同时，方案满足密文匿名性，可以有效地保护收发双方的身份隐私.方案使用不同的密码系统参数，更接近于实际应用环境.与已有异构签密方案相比，方案的效率较高，适合于收发双方身份保密和带宽受限的应用需求.

异构签密；无证书公钥密码；密文匿名；计算Diffie-Hellman困难问题；修改逆计算Diffie-Hellman困难问题

1 引言

签密[1]能够同时保证机密性和认证性，提高“单独实现加密和签名”的计算效率，在车联网等环境中有一定的应用[2,3].现有的大多数签密方案都是基于同一种公钥密码，即发送者和接收者的公钥密码环境相同.随着大数据、云计算等应用的展开，跨平台应用及操作将越来越广泛.为了保证异构(不同)密码环境中消息传输的机密性和认证性，有必要研究异构签密[4～7]问题.

2010年，Sun等[4]首次提出异构签密问题并构造了从传统公钥密码到身份公钥密码(Identity-based Public Key Cryptography,IDPKC)[8]的异构签密方案(TPKI→ IDPKC型).2011年，Huang等[5]构造了IDPKC→TPKI型异构签密方案.2013年，Fu等[6]扩展Sun等人的研究工作，构造了一个IDPKC→TPKI多接收者异构签密方案.同年，Li等[7]提出了新的IDPKC→TPKI型和TPKI→IDPKC型异构签密方案.已有异构签密方案中，IDPKC环境和TPKI环境使用了相同的系统参数，即不同的公钥密码环境未使用不同的系统参数.

为了隐藏发送方和接收方的身份信息，签密方案需要满足密文匿名性.2004年，Libert等[9]基于短签名[10]思想提出了满足密文匿名性的签密方案.2005年Yang等[11]指出Libert方案不满足机密性和密文匿名性，并提出了改进方案，但是该改进方案也不满足密文匿名性.2010年，Li等[12]改进了Yang方案，提出了满足密文匿名性的签密方案.

本文定义了从无证书公钥密码(Certificateless Public Key Cryptography,CLPKC)[13]到传统公钥密码PKI(CLPKC→TPKI)异构签密方案的形式化定义和安全模型，并基于文献[12]提出了满足密文匿名性的CLPKC→TPKI异构签密方案.方案具有以下几个特点：

(1)在随机预言模型下，基于计算Diffie-Hellman(Computational Diffie-Hellman,CDH)困难问题和修改逆计算Diffie-Hellman(modification Inverse Computational Diffie-Hellman,mICDH)困难问题，证明该方案满足签密内部安全模型[14]下的机密性和不可伪造性：即使发送者的私钥泄露，攻击者也不能从密文中恢复明文；接收者的私钥泄露，攻击者也不能伪造密文.

(2)满足密文匿名性.攻击者无法从密文中获得发送方和接收方的身份信息，可以有效地保护收发双方的身份隐私.

(3)方案只需要2个双线性运算，减少了双线性对运算个数.

(4)方案设计了互不相同的密码系统参数，更接近于实际应用环境.

2 CLPKC→TPKI异构签密方案定义

CLPKC→TPKI异构签密需要同时考虑CLPKC和TPKI环境，因此，CLPKC→TPKI异构签密方案必须考虑两种密码环境的建立、密钥生成、CLPKC环境的签密和TPKI环境的解签密等过程.CLPKC→TPKI异构签密方案一般包括以下算法.

(1)CLPKC系统建立算法.该算法由CLPKC系统的KGC运行.输入安全参数l，输出系统主密钥s(KGC的私钥)、系统密钥Ppub(KGC的公钥)和系统参数Params1.KGC公开Ppub和Params1，保密s.

(2)TPKI系统建立及密钥生成算法.PKI系统中的CA生成并发布系统参数Params2.用户产生公/私钥对pki/ski，CA对用户的公钥进行签名并输出用户的证书.

(3)CLPKC部分私钥生成算法.该算法由KGC运行.输入用户身份IDi、系统参数Params1和主密钥s，输出用户的部分私钥Di.

(4)CLPKC密钥生成算法.用户选择秘密值xi，输入身份IDi和系统参数Params1，输出用户的完整私钥Si=(Di,xi)和公钥Pi.

(5)签密算法：输入接收者的公钥pkr，消息m、发送者私钥Ss、系统参数Params1及Params2，输出密文σ.

(6)解签密算法：输入密文σ、接收者私钥skr、系统参数Params1及Params2，输出消息m或者符号“⊥”.其中，符号“⊥”表示密文不合法.

以上算法必须满足一致性约束条件：如果σ= Signcrypt(m,Ss,pkr)，则m=Unsigncrypt(σ,Ps,skr)成立.

3 CLPKC→TPKI异构签密方案安全模型

3.1 不可伪造性 CLPKC→TPKI

异构签密方案的不可伪造性主要考虑无证书密码环境中的两类攻击者AI和AII[13,15].AI表现为一般用户，它利用选定的公钥替换用户原有的公钥实现公钥替换攻击；AII表现为密钥生成中心KGC，它可以计算用户的部分私钥实现KGC攻击.

游戏1 假定F为挑战者，CLPKC→TPKI异构签密方案针对攻击者AI的适应性选择消息和身份的攻击游戏由以下三个阶段组成.

初始阶段：F运行“CLPKC系统建立算法”产生系统参数Params1；F运行“TPKI系统建立及密钥生成算法”获得系统参数Params2和接收者公/私钥对(pkr,skr)，发送Params1、Params2和(pkr,skr)给AI.

攻击阶段：F与AI模拟过程中，能够对以下预言机进行多项式有界次适应性询问.

(1)部分私钥询问：AI提交用户身份IDi，F运行“CLPKC部分私钥生成算法”，获得对应的部分私钥Di并返回给AI.

(2)秘密值询问：AI提交用户身份IDi，F运行“CLPKC密钥生成算法”获得IDi对应的秘密值xi并返回给AI.如果用户IDi的公钥已经被替换，那么让F回答这样的询问是不合理的.

CCOS技术发展过程中最具代表性的事件是其在哈勃空间望远镜(图2)修复过程中的应用。当哈勃空间望远镜进入太空使用时，发现其非球面主镜有2 μm的面形误差，这一瑕疵就造成了原先设计为140亿光年的观测距离直接缩短为40亿光年。在1994年，由Tinsley公司和Itek、Easterm-Kodak等公司通力合作，应用CCOS技术加工出了哈勃望远镜主镜的误差校正镜，对太空中哈勃望远镜进行了修复工作[22-23]。经过修复的哈勃望远镜观测距离达到了120亿光年，至今该误差校正镜的制造仍能代表该领域顶尖水平。

(3)公钥询问：AI输入身份IDi，F运行“CLPKC密钥生成算法”，获得IDi对应的公钥Pi并返回给AI.

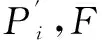
(5)签密询问：AI提交发送者身份IDi、公钥Pi、接收者公钥pkr和消息mi，F调用“CLPKC密钥生成算法”获得IDi的私钥Si，运行“签密算法”并返回密文σ=Signcrypt(mi,Si,pkr)给AI.该询问中，本文采用的是弱无证书签密询问[15]，即如果攻击者替换了用户的公钥，那么要求攻击者提供公钥对应的秘密值.

伪造阶段：AI提交消息m*、发送者身份IDA及公钥PA、接收者公钥pkr及密文σ*，如果以下三个条件成立，则AI赢得该游戏：①σ*对于PA和pkr是一个合法的密文，“解签密算法”执行后不会输出符号“⊥”.②AI没有提交过对IDA的“部分私钥询问”.③AI没有执行对(IDA,m*,pkr)的“签密询问”.

定义1 如果没有任何多项式有界攻击者AI在t时间内，经过以上询问以不可忽略的优势赢得游戏1，那么称该CLPKC→TPKI异构签密方案在适应性选择消息和身份攻击下对于AI攻击安全.

游戏2 假定F为挑战者，CLPKC→TPKI异构签密方案针对攻击者AII的适应性选择消息和身份的攻击游戏由以下三个阶段组成.

初始阶段：F运行“CLPKC系统建立算法”产生系统参数Params1和主秘钥s；运行“TPKI系统建立及密钥生成算法”获得系统参数Params2和接收者公/私钥对(pkr,skr)，发送Params1、Params2、s和(pkr,skr)给AII.

攻击阶段：F与AII模拟过程中，能够对以下预言机进行多项式有界次地适应性询问.

(1)秘密值询问和公钥询问与游戏2相同.由于AII持有系统主密钥，因此，不考虑部分私钥询问，同时不允许AII进行公钥替换询问.

(2)签密询问：AII提交发送者身份IDi及公钥Pi、接收者公钥pkr和消息mi，F调用“CLPKC密钥生成算法”获得IDi的私钥Si，运行“签密算法”并返回密文σ给AII.

伪造阶段：AII提交消息m*、发送者身份IDA及公钥PA、接收者公钥pkr及对应的密文σ*，如果以下三个条件成立，则AII赢得上述游戏：①σ*对于PA和pkB是一个合法的密文，即“解签密算法”执行后不会输出符号“⊥”.②AII没有提交过对IDA的“秘密值询问”.③AII没有执行对(IDA,m*,pkr)的“签密询问”.

定义2 如果没有任何多项式有界攻击者AII在t时间内，经过以上询问以不可忽略的优势赢得游戏2，那么称该CLPKC→TPKI异构签密方案在适应性选择消息和身份攻击下对于AII攻击安全.

注意：游戏1和游戏2允许攻击者可以获得接收者的私钥，这样可以确保方案满足不可伪造性的内部安全性，即使接收者的私钥泄漏，攻击者也不能伪造一个有效的密文.

定义3 如果存在敌手AI和AII以不可忽略的概率在游戏1和游戏2中获胜，则该方案在适应性选择消息和身份攻击下具有存在不可伪造性.

3.2 机密性CLPKC→TPKI

异构签密方案的机密性主要考虑普通攻击者，包括CLPKC和TPKI环境中的任意攻击者.

游戏3 CLPKC→TPKI异构签密方案的适应性选择密文攻击游戏由以下五个阶段组成，该游戏在攻击者A和挑战者F之间进行.

初始阶段：F运行“CLPKC系统建立算法”，产生系统参数Params1和主密钥s；F运行“TPKI建立及密钥生成算法”产生系统参数Params2和接收者的公/私钥对pkr/skr.F发送参数Params1、Params2、主密钥s和接收者的公钥pkr给A.

阶段1：F与A模拟过程中，A能够对签密预言机和解签密预言机进行多项式有界次适应性询问.

签密询问：A提交消息m、发送者私钥Si及接收者公钥pkr，调用“签密算法”生成并返回密文σ=(C,V)给A.

解签密询问：A提交发送者公钥Pi和密文σ给F，F输入接收者私钥skr，运行“解签密算法”并将结果返回给A.

挑战阶段：A决定何时结束“阶段1”并进入“挑战阶段”.A选择两个长度相同的消息m0和m1、发送者身份IDi、接收者公钥pkr作为挑战信息并发送给F.F首先调用“CLPKC密钥生成算法”获得发送者的私钥Ss，然后随机选择b∈{0,1}，对mb执行“签密算法”获得密文σ*=Signcrypt(mb,Ss,pkr)，最后发送σ*给A作为挑战密文.

阶段2：A可以像“阶段1”对以上预言机进行多项式有界次适应性询问，F同样按照“阶段1”那样给出反馈.但是，A不能提交关于σ*的解签密询问.

注意：游戏3允许攻击者能够获得CLPKC环境中用户的完整私钥，这样，可以确保方案满足机密性的内部安全性，即使发送者私钥泄漏，攻击者也不能从密文中恢复出原始消息.

定义4 如果没有任何多项式有界攻击者在t时间内，经过以上询问以不可忽略的优势赢得游戏3，那么称这个CLPKC→TPKI异构签密方案在适应性选择密文攻击下具有密文不可区分性.

3.3 密文匿名性

游戏4 CLPKC→TPKI异构签密方案的密文匿名性游戏由以下五个阶段组成，攻击者A和挑战者F之间进行以下游戏.

初始阶段：F运行“TPKI系统建立及密钥生成算法”生成两个公/私钥对(pkr,0,skr,0)和(pkr,1,skr,1)作为密文接收者，并将公钥pkr,0和pkr,1发送给A.F运行“CLPKC部分私钥生成算法”和“CLPKC密钥生成算法”生成两个公/私钥对(Ps,0,Ss,0)和(Ps,1,Ss,1)作为密文发送者，并将私钥Ss,0和Ss,1发送给A.注意：A可以是任意攻击者.

阶段1：F与A模拟过程中，A能够执行多项式有界次的签密和解签密询问.签密询问时，A提交一个接收者的公钥pkw和消息m给F.如果pkw≠pkr,c，则F运行“签密算法”返回密文σ=Signcrypt(m,Ss,c′,pkw)，其中c∈{0,1}，c′∈{0,1}；如果pkw=pkr,c，返回错误符号“⊥”.解签密询问时，攻击者A提交一个密文σ给挑战者F获得Unsigncrypt(σ,Ps,c′,skr,c)的结果.

挑战阶段：A决定何时结束“阶段1”并进入“挑战阶段”.A选择消息m及发送者的私钥Ss,0和Ss,1.F选择c,c′∈{0,1}并计算σ*=Signcrypt(m,Ss,c′,pkr,c)，发送σ*给A作为挑战密文.

阶段2：A可以像“阶段1”一样进行多项式有界次适应性询问.但是，不能提交对σ*的解签密询问.

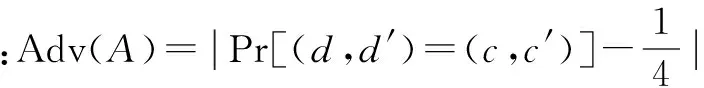
定义5 如果没有任何多项式有界攻击者以不可忽略的优势赢得游戏4，则该CLPKC→TPKI异构签密方案在适应性选择密文攻击下具有密文匿名性.

限于篇幅，本文略去方案中用到的数学基础知识内容，例如CDH困难问题和mICDH困难问题等.

4 具体CLPKC→TPKI异构签密方案

CLPKC→TPKI异构签密方案的算法如下.

(1)TPKI系统建立及密钥生成算法.设k2为TPKI系统安全参数，q2为k2比特的大素数，定义阶均为q2的群GT1和乘法群GT2,生成元P2∈GT1，l2表示GT1元素长度，定义双线性映射e′:GT1×GT1→GT2.发布系统参数Params2={GT1,GT2,q2,P2,e′}.用户产生公/私钥对pki/ski，其中，pki=xiP2.CA生成并发布用户公钥证书.

(2)CLPKC系统建立算法.设k1为CLPKC系统安全参数，q1为k1比特的大素数，定义阶均为q1的加法群G1和乘法群G2，生成元P1∈G1，l1表示G1元素长度，双线性映射e:G1×G1→G2.KGC定义哈希函数

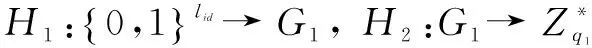
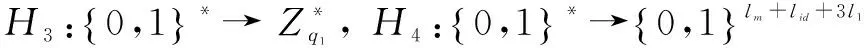
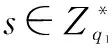
(3)CLPKC部分私钥生成算法.用户提交身份IDi，KGC计算Qi=H1(IDi)和Di=sQi，发送Di给用户.

(5)签密算法.发送者获得接收者的公钥证书(包含公钥pkB=xBPz)后，执行以下过程.

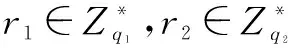
②计算T=r2pkB，h=H3(m,U,PA,V,pkB,T)和W=(r1+h)SA.

③计算C=(m‖IDA‖PA‖W‖U)⊕H4(V,pkB,T)，得到消息m的密文σ=(C,V).

(6)解签密算法：接收者收到密文σ=(C,V)后，执行以下过程.

①计算T′=xBV，恢复包含消息m的比特串(m‖IDA‖PA‖W‖U)=C⊕H4(V,pkB,T′).

②计算yA=H2(PA)，h=H3(m,U,PA,V,pkB,T′)和QA=H1(IDA).

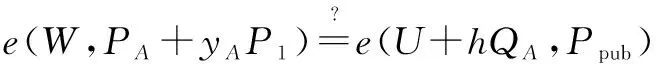
5 安全性分析及效率对比

5.1 不可伪造性

定理1 随机预言模型下，假设CDH问题和mICDH问题困难，则CLPKC→TPKI异构签密方案在适应性选择消息和身份攻击下存在性不可伪造，即适应性选择消息和身份攻击对于AI和AII安全.

引理1 随机预言模型下，如果存在一个攻击者AI能够以ε优势攻破CLPKC→TPKI异构签密方案的AI类安全性，那么存在一个算法F能够以

的优势解决CDH困难问题，其中qpr、qs、qH1和qH3分别表示部分私钥询问、签密询问、H1询问和H3询问的最大次数.

证明AI是攻击者，F是CDH问题挑战者.F给定一个CDH问题实例(P1,aP1,bP1)，F的目标是使用AI解决CDH问题，即计算abP1.

初始阶段：F运行“CLPKC系统建立”算法，产生系统参数Params1，设Ppub=aP1.F运行“TPKI系统建立及密钥生成算法”获得系统参数Params2和接收者公钥/私钥对(pkr,skr).F发送Params1、Params2、挑战身份ID*和接收者公钥/私钥对(pkr,skr)给AI.

攻击阶段：F与AI模拟过程中，F维护列表L1～L4、L=(IDi,xi,Pi,c)和L′=(IDi,Di)保存H1～H4预言机询问、公钥询问、秘密值询问和部分私钥询问过程中产生的数据，所有列表初始为空.AI能够对以下预言机进行多项式有界次地适应性询问.

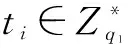
H4询问：F保持列表L4=(Vi,pkr,Ti,ωi)，AI询问H4预言机，首先检查L4中是否存在元组(Vi,pkr,xrVi).若存在相应项，则直接返回结果ωi；否则随机选择ωi∈{0,1}lm+lid+3l1，返回ωi给AI，并且将(Vi,pkr,xrVi,ωi)增加到表L4.

秘密值询问：F保持列表L=(IDi,xi,Pi,c)，AI输入身份IDi，若列表L中存在元组(IDi,xi,Pi,c)并且c=1，则直接返回xi；若列表L中存在元组但c=0，则用户的公钥已被替换，终止该询问并返回.若列表L中不存在元组，F执行“公钥询问”获得并返回xi.

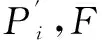
部分私钥询问：F保持列表L′=(IDi,Di)，AI输入身份IDi，然后执行以下过程：①若IDi=ID*，则F失败并终止.②若IDi≠ID*，并且若列表L′中存在对应部分私钥信息，则直接返回；否则，F检查表L1获得ti值，计算Di=tiaP1，返回Di给AI并将(IDi,Di)增加到表L′.

签密询问：AI提交发送者身份IDs、接收者公钥pkr和消息m，执行以下过程：

(II)若IDs=ID*，F调用“TPKI系统建立及密钥生成”算法获得接收者的公/私钥对(pkr=xrP2,xr).F从L1和L2中获得(IDi,Qi,ti)和(IDi,xi,Pi,c)，然后执行以下过程：

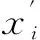
伪造阶段：AI输出消息m、发送者身份IDs及公钥Ps、接收者公钥/私钥(pkr,skr=xr)和密文σ*=(C*,V*)：

①若IDs≠ID*则F失败终止，F不能解决CDH困难问题.②若IDs=ID*，根据分叉引理[16]，F选择不同的哈希函数H3获得h′，并再次利用AI获得另一个有效的密文σ′=(C′,V′)，其中h′≠h，则有以下等式成立：

(m‖IDs‖Ps‖W‖U)=C*⊕H3(V*,pkr,xrV*)

和

e(W,Ps+ysP1)=e(U+hQs,Ppub)

及

(m‖IDs‖Ps‖W′‖U)=C′⊕H3(V′,pkr,xrV′)

和

e(W′,Ps+ysP1)=e(U+h′Qs,Ppub)

并且，

h=H3(m,U,Ps,V*,pkr,xrV*)，

h′=H3(m,U,Ps,V′,pkr,xrV′).

则有以下等式成立：

e(W-W′,Ps+ysP1)=e(hQs-h′Qs,Ppub)，

e((xs+ys)(W-W′),P1)=e((h-h′)abP1,P1).

获得CDH问题的一个解：

定义E1为“部分私钥询问过程未终止”事件，E2为“签密询问过程未终止”事件，E3为“成功伪造一个合法密文”事件，E4为“E3发生的条件下，存在IDs=ID*，分叉引理使用成功，得到CDH困难问题的一个解”事件.如果以上事件都发生，则F成功解决CDH问题，其优势可定义为：

Pr[E1∧E2∧E3∧E4]=Pr[E1]Pr[E2|E1]Pr[E3|E2∧E1]

对于部分私钥询问，若IDi=ID*则终止，容易计算部分私钥询问未终止的概率为(1-1/qH1)，则Pr[E1]≥(1-1/qH1)qpr.

对于签密询问，若H3(m,U,Pi,V,pkr,xrV,h)的值已经存在，那么F将终止，则H3值不存在的概率为(1-qs/2poly(k1))，则Pr[E2|E1]≥(1-qs/2poly(k1))qH3.

又因为Pr[E3|E2∧E1]=ε，则

Pr[E1∧E2∧E3∧E4]

其中qpr、qs、qH1和qH3分别表示部分私钥询问、签密询问、H1哈希询问和H3哈希询问的最大次数.

引理2 随机预言模型下，如果存在一个攻击者AII能够以ε的优势攻破CLPKC→TPKI异构签密方案的AII类安全性，那么存在一个算法F能够以

的优势解决mICDH困难问题，其中qsv、qs和qH3分别表示秘密值询问、签密询问和H3询问的最大次数.

证明AII是攻击者，F是mICDH问题挑战者.F给定一个mICDH问题实例(P1,aP1,b)，F的目标是使用AII解决mICDH问题，即计算(a+b)-1P1.

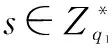
攻击阶段：F与AII模拟过程中，F维护列表L1～L4、L=(IDi,xi,Pi)和L′=(IDi,Di)，保存H1～H4询问、公钥询问、秘密值询问过程中产生的数据，所有列表初始为空.AII能够对以下预言机进行多项式有界次地适应性询问.

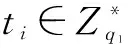
H3询问、H4询问：与引理1证明过程中H3询问和H4询问过程相同.

秘密值询问：AII输入身份IDi，F检查表L是否存在身份IDi.若存在则F返回xi，否则执行过程：①若IDi=ID*，则β≠⊥′且xi=⊥，F失败并终止.②若IDi≠ID*，则β=⊥′且xi≠⊥，F返回xi.

签密询问：AII提交发送者的身份IDs、接收者公钥pkr和消息m，执行以下过程：

伪造阶段：AII输出消息m、发送者的身份IDs、发送者公钥Ps、接收者公钥/私钥对(pkr,skr)和密文σ*=(C*,V*)：①若IDs≠ID*则F失败终止，不能解决mICDH困难问题.②若IDs=ID*，根据分叉引理[16]，F选择不同的哈希函数H3获得h′，并再次利用AII的能力，获得另一个有效的密文σ′=(C′,V′)，其中，h′≠h.与引理1相似，有以下等式成立：

e(W-W′,Ps+ysP1)=e(hQs-h′Qs,Ppub)

e(W-W′,βaP1+βbP1)=e((h-h′)stsP1,P1)

因此，可以获得mICDH问题的一个解：

与引理1相似，F成功解决mICDH问题的优势为

其中qsv、qs和qH3分别表示秘密值询问、签密询问和H3询问的最大询问次数.

5.2 机密性

定理2 随机预言模型下，如果存在一个攻击者A能够以ε的优势攻破CLPKC→TPKI异构签密方案，那么存在算法F能够以2ε(1-qu/2poly (k2))的优势解决CDH困难问题，其中qu表示解签密最大询问次数，k2为TPKI系统安全参数.

5.3 密文匿名性

由于定理2和定理3的证明过程与文献[12]相似，限于文献篇幅，略去它们的证明过程.

5.4 效率分析

公开文献显示当前没有CLPKC-TPKI异构签密方案，因此，无法与同类CLPKC→TPKI异构签密方案进行效率比较.文献[7]的IDPKC→TPKI异构签密方案是当前效率最高的异构签密方案，本节对比两个方案的效率.用e表示幂运算个数，P表示双线性对运算个数.由表1可知，本文方案的计算效率优于文献[7]方案.

表1 效率对比

6 小结

一般而言，签密方案默认发送方和接收方具有相同的密码环境.但是，在许多应用中，发送方和接收方可能处于不同的密码环境，即异构密码环境.本文定义了CLPKC→TPKI异构签密的形式化定义和安全模型，设计了一个CLPKC→TPKI异构签密方案.在随机预言模型下，证明方案能够满足签密的内部安全性.方案中CLPKC和TPKI密码环境具有互不相同的参数.同时，方案满足匿名性，任何人都不能获得密文收发双方的身份信息，该特性可以满足无线移动匿名接入的要求.

[1]Zheng Y L.Digital signcryption or how to achieve cost (signature & encryption)<

[2]Ma Z,Li F H,Ma J F,et al.CL-TAP:An efficient certificateless based trusted access protocol for WLAN[J].Chinese Journal of Electronics,2014,23(1):142-146.

[3]张宇,陈晶,杜瑞颖,等.适于车载网安全通信的高效签密方案[J].电子学报,2015,43(3):512-517.

Zhang Yu,Chen Jing,Du Rui-ying,et al.An efficient signcryption scheme for secure communication of VANET[J].Acta Electronica Sinica,2015,43(3):512-517.(in Chinese)

[4]Sun Y X,Li H.Efficient signcryption between TPKI and IDPKC and its multi-receiver construction[J].Science China Information Sciences,2010,53(3):557-566.

[5]Huang Q,Wong D S,Yang G M.Heterogeneous signcryption with key privacy[J].The Computer Journal,2011,54(4):525-536.

[6]Fu X T,Li X W,Liu W.IDPKC-to-TPKI construction of multi-receiver signcryption[A].Proceedings of the INCoS(5)[C].Xian:IEEE,2013.335-339.

[7]Li F G,Zhang H,Takagi T.Efficient signcryption for heterogeneous systems[J].IEEE Systems Journal,2013,7(3):420-429.

[8]Shamir A.Identity-based cryptosystems and signature schemes[A].Advances in Cryptology[C].Heidelberg:Springer,1985.47-53.

[9]Libert B,Quisquater J.Efficient signcryption with key privacy from gap Diffie-Hellman groups[A].Advances in Public Key Cryptography-PKC[C].Berlin,Springer,2004.187-200.

[10]Boneh D,Lynn B,Shacham H.Short signatures from the Weil pairing[A].Advances in Cryptology-Asiacrypt[C].Berlin:Springer,2001.514-532.

[11]Yang G M,Wong D S,Deng X T.Analysis and improvement of a signcryption scheme with key privacy[A].Advances in Public Key Cryptography-PKC[C].Berlin,Springer,2005.218-232.

[12]Li C K,Yang G M,Wong D S,et al.An efficient signcryption scheme with key privacy and its extension to ring signcryption[J].Journal of Computer Security,2010,18(3):451-473.

[13]Al-Riyami S,Paterson K.Certificateless public key cryptography[A].Advances in the Cryptology-Asiacrypt[C].Berlin:Springer,2003.452-474.

[14]An J H,Dodis Y,Rabin T.On the security of joint signature and encryption[A].Advance in Cryptography-EUROCRYPT[C].Berlin,Springer,2002.83-107.

[15]Barbosa M,Farshim P.Certificateless signcryption[A] Proceedings of the ACM Symposium on Information,Computer and Communications Security (ASIACCS)[C].Tokyo:ACM,2008.69-372.

[16]Pointcheval D,Jacques S.Security proofs for signature schemes[A].Advances in Cryptology-Eurocrypt[C].Berlin:Springer,1996.387-398.

张玉磊 男，1979年出生于甘肃靖远，博士，西北师范大学计算机科学与工程学院副教授，硕士生导师.研究方向为网络与信息安全、密码学、安全协议分析与设计.

E-mail:zhangyl@nwnu.edu.cn

张灵刚 男，1990年出生于甘肃省灵台县，西北师范大学计算机科学与工程学院硕士生.研究方向为网络与信息安全.

E-mail:linggang01@126.com

张永洁(通信作者) 女，1978年出生于甘肃武都，硕士，甘肃卫生职业学院副教授.研究方向为网络与信息安全.

E-mail:zyjie78@163.com

王 欢 女，1991年出生于河北省枣强县，西北师范大学计算机科学与工程学院硕士生研究生.研究方向为网络与信息安全.

E-mail:1530749678@qq.com

CLPKC-to-TPKI Heterogeneous Signcryption Scheme with Anonymity

ZHANG Yu-lei1,ZHANG Ling-gang1,ZHANG Yong-jie2,WANG Huan1,Wang Cai-fen1

(1.CollegeofComputerScienceandEngineering,NorthwestNormalUniversity,Lanzhou,Gansu730070,China;2.GansuHealthVocationalCollege,Lanzhou,Gansu730000,China)

Heterogeneous signcryption,a cryptographic primitive,can simultaneously provide the confidentiality and unforgeability of data transmission between different public key cryptography.The paper gives the definition and security models of CLPKC-to-TPKI heterogeneous signcryption scheme between CLPKC (Certificateless Public Key Cryptography) and TPKI (Traditional Public Key Infrastructure),and presents a construction by using the bilinear pairing.In the random oracle model,based on the assumptions of Computational Diffie-Hellman and modifying Inverse Computational Diffie-Hellman,the scheme is proved to satisfy the confidentiality and unforgeability of the insider security.Moreover,it satisfies the properties of ciphertext anonymity which can efficiently protect the privacies of sender and receiver.Owing to the independence and difference of the system parameters in CLPKC and TPKI,the scheme is more suitable in the practical environments.Furthermore,the analysis of efficiency shows that,comparing to the existing heterogeneous signcryption schemes,the scheme is more efficient,so it is suitable for the requirements of identity hiding and constrained bandwidth.

heterogeneous signcryption;certificateless public key cryptography;ciphertext anonymity;computational Diffie-Hellman problem (CDH);modification inverse computational Diffie-Hellman problem(mICDH)

2015-06-17；

2015-12-23；责任编辑：孙瑶

国家自然科学基金(No.61163038，No.61262056，No.61262057)；甘肃省高等学校科研项目(No.2015B-220，No.2013A-014)；西北师范大学青年教师科研能力提升计划项目(No.NWNU-LKQN-12-32)

TP309

A

0372-2112 (2016)10-2432-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.022