基于多元统计分析的浙江省水资源承载力综合评价
2016-12-08周丽
周 丽
(温州大学数学与信息学院,浙江 温州 325035)
基于多元统计分析的浙江省水资源承载力综合评价
周 丽
(温州大学数学与信息学院,浙江 温州 325035)
建立浙江省水资源承载力评价指标体系,运用主成分分析法和聚类分析法,对浙江省2000—2013年水资源承载力的演变趋势展开纵向演变分析。结果表明:社会经济环境综合承载因子和水资源承载因子是影响浙江省水资源承载力的关键因子;浙江省水资源承载力整体表现为逐年波动上升的趋向,2000—2002年水资源承载力低水平阶段,2003—2009年为平稳发展阶段,2010—2013年为振荡阶段。最后提出提高浙江省水资源承载力的措施与建议。
主成分分析;聚类分析;综合评价;水资源承载力;浙江省
1 问题的提出
水资源承载力是一项衡量社会经济可持续发展的重要指标。“承载力”一词原为物理学概念,物体在不产生任何破坏时的最大极限负荷,水资源承载力是各类资源承载力研究中最活跃的一支[1-2]。目前水资源承载力没有统一定义,典型代表如夏军等认为水资源承载力是指在一定的水资源开发利用阶段,满足生态需求的可利用水量能够维系有限发展目标的最大的社会经济规模[3-4]。水资源承载力的研究主要有2个层面[5]:一是承载状态评价;二是承载规模预测。水资源承载力研究方法还处于不断尝试与探索阶段,主要有常规趋势法、模糊评价分析法、系统动力学方法、多目标决策分析法、主成分分析法等[6-11]。水资源承载力研究已成为当前水资源科学研究中的热点问题。
浙江省一直走在我国经济和社会发展的前沿,是经济强省、科技强省。经济快速增长的同时,对于水资源的需求程度也相应增加。为寻求社会经济的可持续发展,必须对水资源承载力进行研究。目前以浙江省作为研究对象的水资源承载力研究的文献数量极少[11-13]。针对浙江省的水资源承载力进行实证研究还是非常有现实意义的。
本文以浙江省为例,利用主成分分析、聚类分析等多元统计方法,从时间角度对浙江省水资源的承载状态进行评价;根据分析结果提出提高浙江省水资源承载力水平的对策与建议,对促进浙江地区水资源、社会、经济、环境的可持续协调发展具有长远意义,为政府部门进行浙江省区域发展规划、水资源规划与管理及“五水共治”行动等的科学决策提供参考依据。
2 材料与方法
2.1 指标选取原则
水资源承载力的研究起步较早,多方原因使得目前有关概念和内涵尚未达成较为一致的共识,因此一个核心的焦点问题是指标体系构建的合理性。考虑到区域水资源承载力综合评价是对区域水资源、社会、生态与经济协调持续发展状况进行综合评价研究,因此水资源承载力指标体系是一个复杂的大系统,指标选取时应以可持续发展为指导思想,从“水资源—社会经济—生态环境"复合系统的视角,遵循如下原则:
(1)科学性原则:即按照科学理论,特别是可持续发展理论定义指标的概念和内涵。
(2)代表性原则:即从水资源自身系统及其相关的社会、经济、生态、环境等各个子系统的基础指标中,根据指标具体定义和量化计算,最终选择出能从本质上全面反映研究对象的关键性指标。
(3)可行性原则:即指标内容应简单明了,具有可比性,并充分考虑资料收集时的可行性。
2.2 指标体系
水资源承载力受到多种因素的影响,其中最主要的因素涉及经济、社会、环境等。在各影响因素中选取最科学全面的、最有代表性的和可行性的指标。参照全国水资源供需平衡分析中的指标体系以及前人研究的基础上,选取以下11个指标构成评价体系(见表1)。
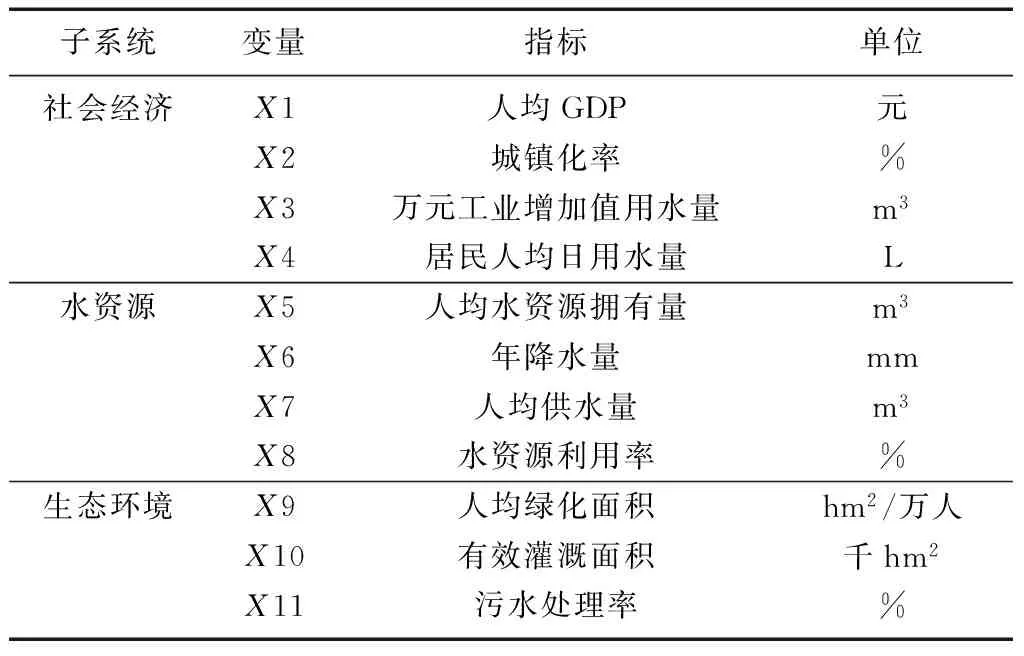
表1 浙江省水资源承载力评价指标体系表
2.3 研究方法
主成分分析方法是多元统计中目前理论和应用都较为成熟完善的描述性方法,本文主要探讨主成分分析方法、聚类分析等多元统计分析技术在水资源承载力综合评价中的应用。
2.3.1 主成分分析法简介
主成分分析[14-15](principal component analysis,简记为PCA)是将多指标化为少数指标的一种多元统计分析方法。基本思想是 通过降维技术将原来众多具有相关性的多个指标,重新组合成一组较少个数且互不相关的综合指标来代替原有指标。这些综合指标就是主成分,它们保留了原始变量绝大部分信息,通常表示为原始变量的线性组合。通过主成分分析,可以实现将高维空间的问题转化为低维空间来处理。
假设有n个样品的p个指标变量X1,X2,X3,…,Xp,记X=(X1,X2,X3,…,Xp)′,对X进行线性变换,可以生成新的综合指标f1,f2,f3,…,fp,即为p个主成分。其数学模型为:
(1)
式中:iji是第i个主成分fi在第j个变量xj上的载荷,体现两者之间线性相关程度。
主成分分析法的计算步骤为:

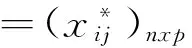
(3)求R阵的特征值λ1>λ2>…>λp及正则化单位特征向量e1,e2,…,ep其中每一特征向量为对应主成分的线性表达式中原始数据的组合系数,即第i个主成分表达式为:
fi=e1ix1*+…+epixp*
(2)
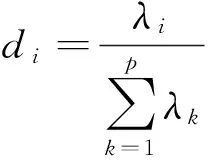
(5)将各待评样品的标准化数据分别代入各主成分的表达式中,计算出样品的各主成分得分fi,以方差贡献率为权数求和得综合得分:
f=d1f1+d2·f2+…+dm·fm
(3)
2.3.2 聚类分析法简介
聚类分析法[14-15]是研究“物以类聚”的一种现代统计分析方法,聚类分析的目的是把分类对象按一定规则分成若干类,按照具体方法不同划分为系统聚类法、快速聚类法、模型聚类法。
系统聚类法是众多聚类分析方法中用得最多的一种方法,其基本思想是:开始将n个样品各自作为一类,并规定样品之间的距离和类与类之间的距离,然后将距离最近的2类合并成1个新类,计算新类与其它类的距离,重复进行2个最近类的合并,每次减少1类,直到所有的样品合并为1类。系统聚类法中类与类之间距离的计算方法具体有多种:最短距离法、最长距离法、中间距离法、类平均法、可变法、可变类平均法、重心法、离差平方和法(Ward方法)等。
系统聚类法的基本步骤:
(1)计算n个样品两两间的距离{dij},记作D;
(2)构造n个类,每个类只包含1个样品;
(3)合并距离最近的2类为1个新类;
(4)计算新类与当前各类的距离,若类个数为1,转到步骤(5),否则回到步骤(3)。
(5)画聚类谱系图,决定类的个数和类。
3 结果与分析
3.1 指标数据及来源说明
根据2.2节选取的11个指标,收集了2000—2013年的浙江省数据(见表2)。数据资料来自于《浙江统计年鉴》(2001—2014)、《浙江省水资源公报》(2000—2013),部分数据经过计算整理获得。
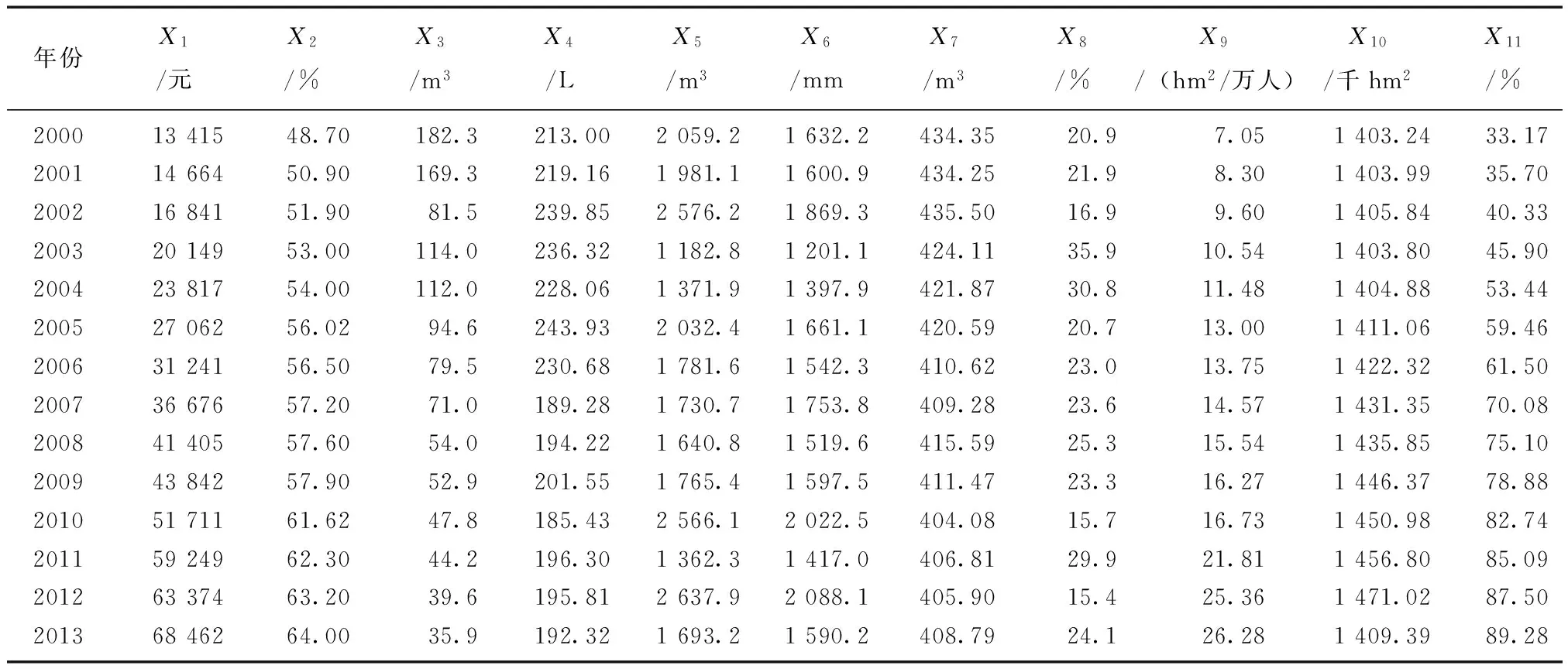
表2 浙江省水资源承载力纵向综合评价的原始数据(2000—2013年)表
3.2 主成分分析法在浙江省水资源承载力纵向综合评价中的应用
3.2.1 计算过程
(1)标准化处理。对表2中的原始数据利用统计软件R的scale()函数[15],可实现标准化处理。
(2)计算相关系数矩阵。对标准化后的数据利用统计软件R的Princomp函数,可实现主成分分析计算,输出相关系数矩阵、特征值与特征向量.
从相关系数矩阵可知,评价指标彼此间存在高度的相关性,如X1*和X2*、X9*、X11*相关系数分别为0.980、0.978和0.965,X2*和X7*、X11*间相关系数分别为-0.915,0.974。指标之间只有存在较高的相关性才能够应用主成分方法展开分析,故可以验证主成分分析的必要性。

表3 载荷矩阵表
由特征值看出,前2个主成分累计贡献率为88.18%,故只需提取2个主成分代表原始数据进行分析。表3中载荷矩阵(相关系数)是由提取的每个主成分的特征向量乘以对应的特征值的平方根得到的,表示每个主成分与指标变量间的线性相关程度。从表3看出:
(1)第一主成分和X1*、X2*、X9*、X10*、X11*之间有较强的正相关关系,和X3*、X4*、X7*之间有较强的负相关关系。第一个主成分包含62.98%的信息量,主要涵盖了社会经济、生态环境的主要指标,因此可称为“社会经济环境综合性承载因子”。从社会经济子系统来看,随着浙江省经济水平快速进步,水资源承载力也会随着人均GDP以及城镇化率的不断提高而提高。从生态环境子系统来说,社会经济和科技水平快速发展,居民环保意识不断增强,城市绿化覆盖面积逐年增加以及有效灌溉面积总体上升,反映了生态环境的改善和水资源利用率的提高,推动其承载力发展空间的提升。
(2)第二主成分和X5*、X6*之间有较强的正相关关系,和X8*有较强的负相关关系。第二个主成分的贡献率为23.237%,基本涵盖了水资源条件因素,故称为“水资源承载因子”。地区自身水资源条件如年降水量、人均占有量等是影响水资源承载力的关键因素,更为浙江省水资源起到了补给和保障作用。根据前2个主成分对应的特征向量,直接得到前2个主成分f1和f2的表达式,并以方差贡献率为权数对其求和得综合得分f的表达式,分别见公式(4)和(5)。将各年标准化处理后数据分别代入各主成分的表达式中,便计算得各主成分得分,进而可得综合得分和排名,最终结果见表4和图1。
(4)
f=0.714 3f1+0.285 7f2
(5)
表4 浙江省水资源承载力评价的综合得分及排名表
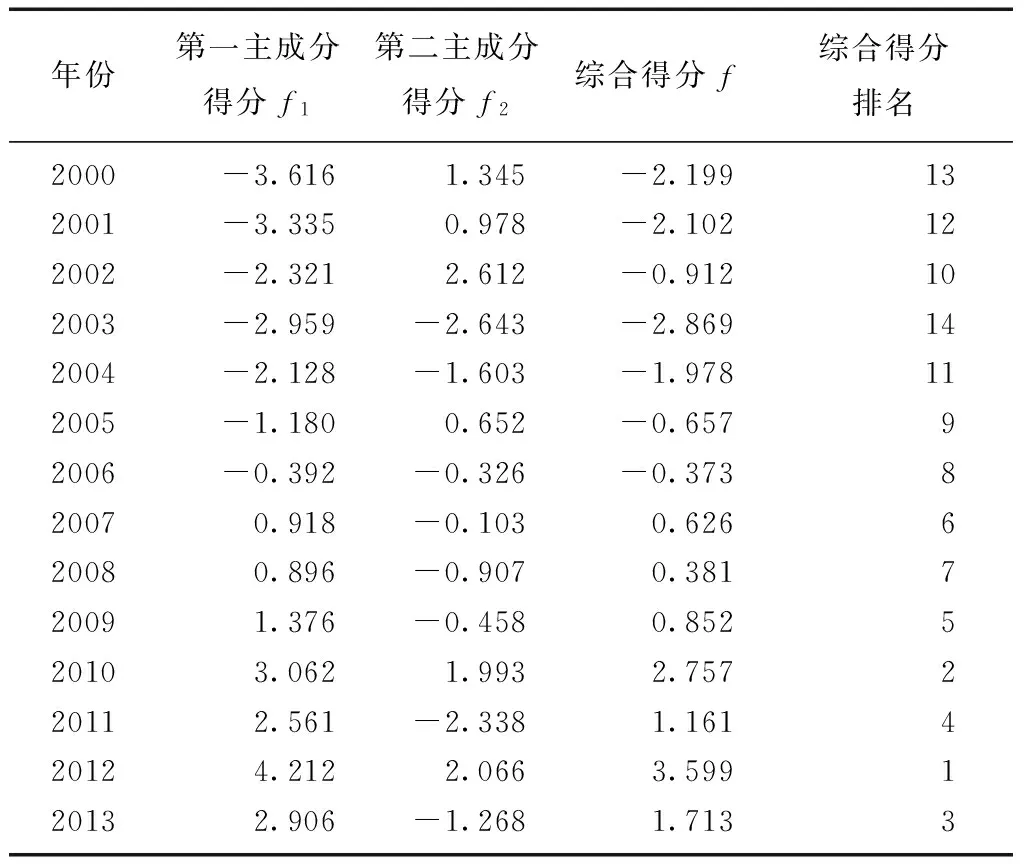
年份第一主成分得分f1第二主成分得分f2综合得分f综合得分排名2000-3.6161.345-2.199132001-3.3350.978-2.102122002-2.3212.612-0.912102003-2.959-2.643-2.869142004-2.128-1.603-1.978112005-1.1800.652-0.65792006-0.392-0.326-0.373820070.918-0.1030.626620080.896-0.9070.381720091.376-0.4580.852520103.0621.9932.757220112.561-2.3381.161420124.2122.0663.599120132.906-1.2681.7133

图1 浙江省水资源承载力各个主成分及综合得分走势图
3.2.2 结果分析
表4中各主成分得分和综合得分有正有负,正负表示历年相对值,取正表示在平均水平之上,取负表示低于平均水平,得分值越大,表示水资源承载能力越大。由图1可直观看到:①第一主成分得分f1表现为逐年波动升高的走势,表明浙江省这10多年来社会经济环境承载能力总体上是稳中逐步上升;②第二主成分得分f2基本上围绕平均水平线上下摆动,说明浙江省的水资源状况随着时间变化基本持平,最近这4 a水资源条件变化很大,忽高忽低,是由于这几年的降雨量和人均供水量特别高或特别低造成的;③从综合得分f上看,浙江省水资源承载力情况总体表现也是逐年波动升高的走势,图1中第一主成分得分f1和综合得分f这2条曲线的走势无太大差别,主要原因在于第一个主成分的贡献率高达62.98%,基本与总体趋势相一致,成为浙江省水资源承载力在时间维度上最重要因子。随着浙江省经济社会的持续快速发展,以及政府相关部门对水问题越来越重视,并且加大财政资金以及技术的投入,使得浙江省生态环境的大大改善,水资源的利用效率和污水处理率逐年上升,政府加大宣传力度使得人们增强节水意识,种种举措将有效提升承载力。
3.3 聚类分析法在浙江省水资源承载力纵向综合评价中的应用
3.3.1 计算过程
聚类分析前也一样要对原始数据进行标准化处理,所以可以直接对标准化处理后的数据,利用R软件R3.1.1的dist()函数计算“ Euclid”距离,然后用hclust()函数进行系统聚类[15]。本文选择最长距离法,以分3类较合适,聚类结果谱系见图2。
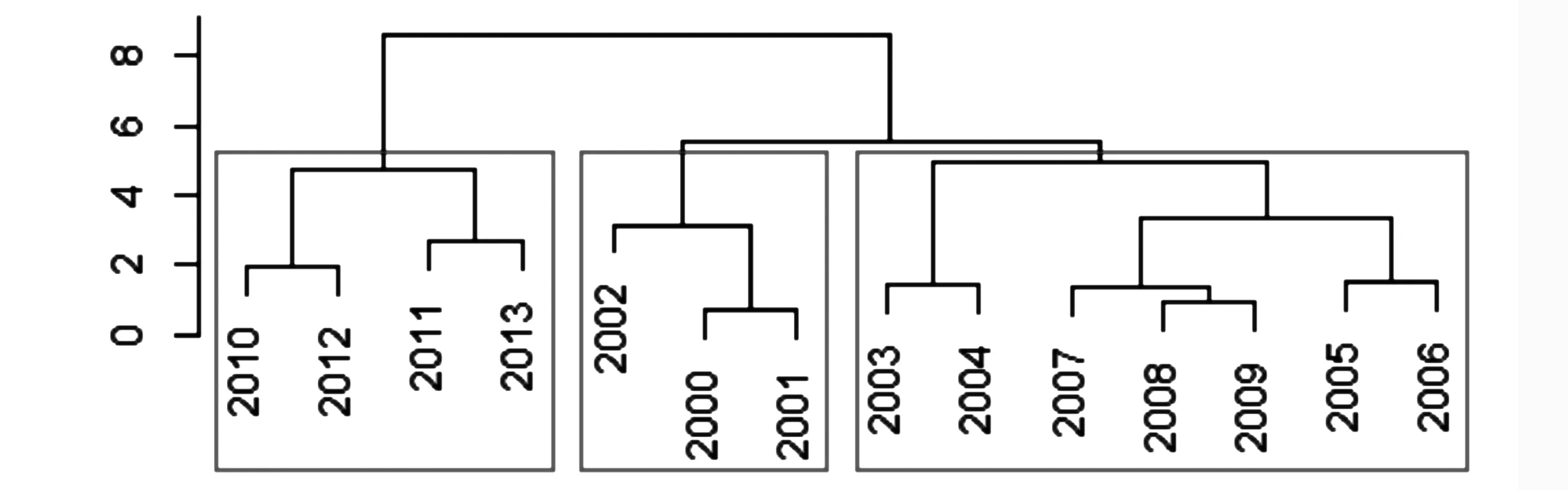
图2 2000—2013年浙江省水资源承载力的系统聚类最长距离法结果谱系图
3.3.2 结果分析
从图2中可知浙江省水资源承载力评价,2000—2002年是第Ⅰ类,2003—2009年为第Ⅱ类,2010年开始的后4 a为第Ⅲ类。主成分分析得出的综合得分是连续性值,无法判定承载力等级,而聚类分析只能得出各个类别,而不能指明各个类别之间的区别,因此可将聚类分析结果与主成分分析结果综合起来分析。将上节主成分分析结果中各年份的第一主成分得分和第二主成分得分(表4的第二列与第三列)分别作为横、纵坐标作散点图,并结合各年份的聚类结果加以标记绘出图3。
由图3可知,从横轴(f1)上看,3个类别对应的第一个主成分相差很大,第一类最小,第二类在平均水平0附近(除2003年外),第三类的值最大,有依类别增大的趋势;从纵轴(f2)上看,第一类的值高于平均水平,第二类基本分布在水平线附近(除2003年外),第三类的值波动很大,要么特别大要么特别小。也就是说,2000—2002年的社会经济环境综合性因子承载能力低,但水资源因子承载能力强,2003—2009年的社会经济环境综合性因子和水资源因子基本都处平均水平,2010年开始的后4 a间的社会经济环境综合发展明显高于2010年前,但水资源因子承载能力剧烈振荡,这些结论与图1中对应一致。可见聚类结果中3个类别的区别主要在于它们的社会经济环境综合承载能力(即第一主成分f1)的值高低不同,这是因为第一主成分从权重上占了0.714 3。再结合图1和表4中的主成分得分,可见聚类结果中的第Ⅲ类的主成分得分最高,第Ⅰ类最低,第Ⅱ类居中,所以把浙江省水资源承载力在时间维度上的变化趋势划分为3个阶段:低水平阶段(2000—2002年)、平稳发展阶段(2003—2009年)、振荡阶段(2010—2013年)。
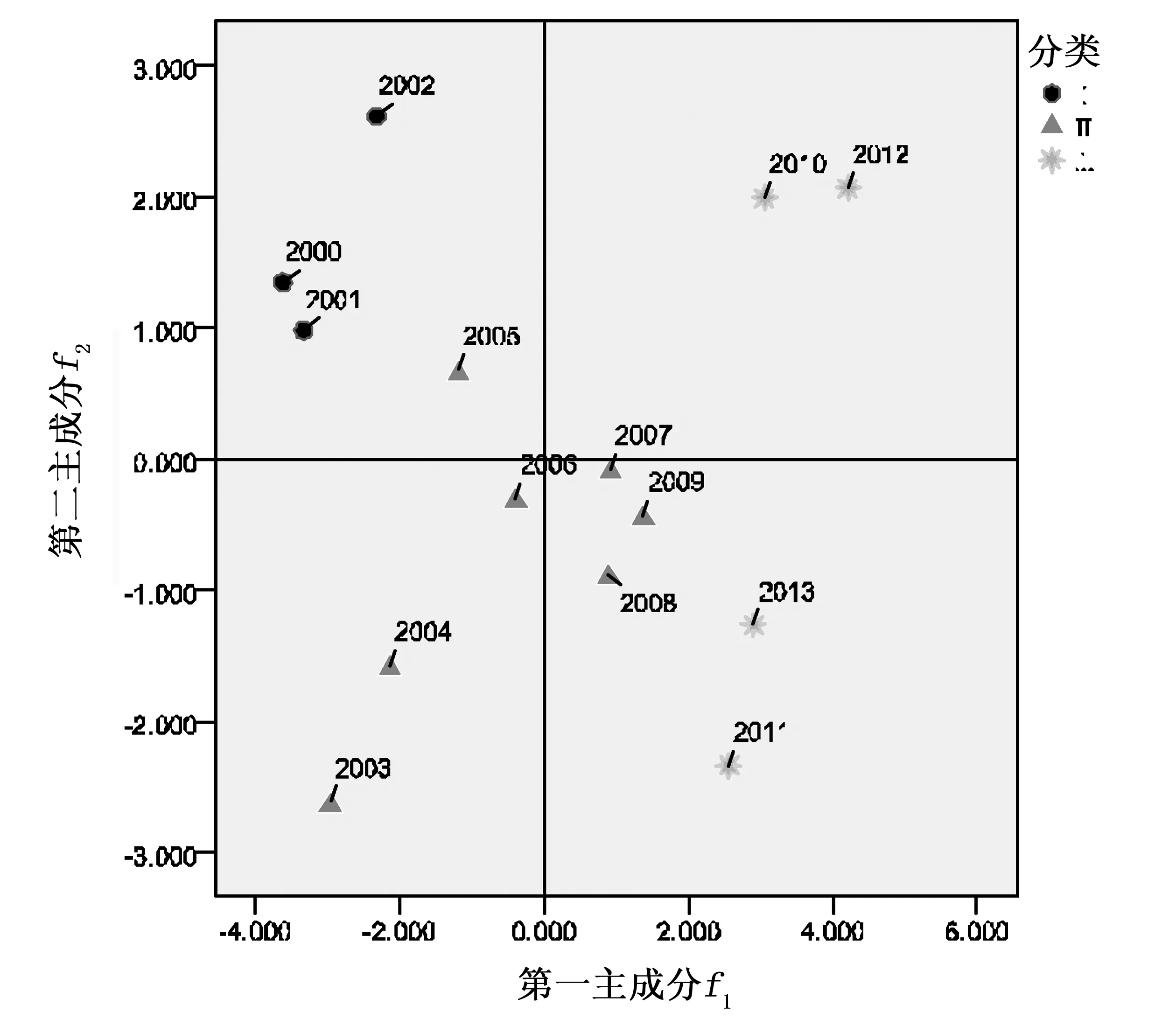
图3 聚类分析的3个类别对应的前2个成分散点图
4 结论与建议
(1)应用多元统计中的主成分分析和聚类分析,分别对浙江省水资源承载力进行综合评价,较客观的表明了浙江省水资源承载力在时间角度的变化趋向。分析结果表明,水资源承载力主要影响因子为社会经济环境综合因子和水资源自然条件因子,其中社会经济环境综合因子影响程度最大。
(2)主成分分析表明,浙江省水资源承载力在时间维度上总体呈现上升趋势,结合聚类分析划分2000—2002年为水资源承载能力低水平阶段,2003—2009年为水资源承载力平稳发展阶段,2010—2013年为水资源承载力振荡阶段。2010年开始的4 a来由于自然条件(降雨量)呈现具现忽高忽变化,引起水资源承载力也随之起伏变化。
(3)浙江省应把人口和经济发展规模控制在社会和资源所能承载的范围内,在制定政策时应更多地考虑各方面的承载力,才能使出台的政策更为合理可行,因此水资源承载能力预测是水资源承载力评价的后续课题。
[1]郭秀锐,毛显强.中国土地承载力计算方法研究综述[J].地球科学进展,2000,15(6):705-711.
[2]龙腾锐,姜文超,何强.水资源承载力内涵的新认识[J].水利学报,2004(1):38-45.
[3]新疆水资源软科学课题研究组.新疆水资源及其承载力的开发战略对策[J].水利水电技术,1989(6):2-6.
[4]夏军,朱一中.水资源安全的度量:水资源承载力的研究与挑战[J].自然资源学报,2002,17(3):262-269.
[5]王占永.城市水资源承载力评价预测模型及软件开发[D].上海:华东师范大学,2010.
[6]施雅风,曲耀光.乌鲁木齐河流域水资源承载力及其合理利用[M]北京:科学出版社,1992.
[7]郭旋,冯利华.义乌市水资源承载力模糊综合评价[J].安徽农业科学,2008,36( 8):3348-3349.
[8]惠泱河,蒋晓辉,黄强,等.二元模式下水资源承载力系统动态仿真模型研究[J].地理研究,2001,20(2):191-198.
[9]方国华,胡玉贵.区域水资源承载能力多目标分析评价模型及应用[J].水资源保护,2006,22(6):9-13.
[10]许朗,黄莺,刘爱军.基于主成分分析的江苏省水资源承载力研究[J].长江流域资源与环境,2011,20(12):1468-1473.
[11]陈腊娇,冯利华,毛小军.主成分分析法在水资源承载力影响因子评价的应用[J].水利科技与经济,2006,12(6):362-364.
[12]卜楠楠,唐德善,尹笋.基于AHP法的浙江省水资源承载力模糊综合评价[J].水电能源科学,2012,30(3):42-46.
[13]汤冠华,刘永.基于生态足迹模型的浙江省水资源生态承载力评价研究[J].浙江水利科技,2013,185(1):45-48.
[14]王晓鹏,曹广超.基于多元统计和GIS的环境质量评价研究[M].北京:科学出版社,2013.
[15]王斌会.多元统计分析与R语言建模[M].广州:暨南大学出版社,2010.
(责任编辑 姚小槐)
Comprehensive Evaluation on the Water Resources Bearing Capacity of Zhejiang Province Based on Multivariate Statistical Analysis
Zhou Li
(Mathematics and Information Institute of Wenzhou University, Wenzhou 325035, Zhejiang, China)
In this paper, an evaluation index system of water resources bearing capacity in Zhejiang Province was established. The principal component analysis and cluster analysis methods were used to analyze the longitudinal evolution of the water resources bearing capacity of Zhejiang province from 2000 to 2013. The results show that comprehensive carrying factor of social, economic and environment, and water resources carrying factor are the main factors affecting the water resources bearing capacity of Zhejiang province, which showed an integral trend that vibrating and rising year by year. The water resources bearing capacity was at a lower level stage between 2000 and 2002, at a steady developing stage between 2003 and 2009, and at a vibrating stage between 2010 and 2013. Finally, it put forward some suggestions that can improve the water resources bearing capacity of Zhejiang province.
principal component analysis;cluster analysis;comprehensive evaluation;water resources bearing capacity;Zhejiang Province
2015-10-19
浙江省科技厅软科学研究计划项目(2014C35079);浙江省统计局2014年度统计研究课题(编号23);浙江省教育厅高校科研计划项目(Y201120738)。
周 丽(1977-),女,讲师,硕士,主要从事水资源系统分析和应用统计等方面的研究。
TV149
A
1008-701X(2016)01-0048-05
10.13641/j.cnki.33-1162/tv.2016.01.016
