“二次函数与一元二次方程”课堂实录

■李长春

课堂实录

“二次函数与一元二次方程”课堂实录

■李长春

一、创设情境，发现问题

（课前，多媒体播放歌曲《隐形的翅膀》，不少学生跟着旋律哼唱）

师：李老师来自东台市实验中学，今天在时堰中学和大家一起交流、学习，我有一种特别亲切的感觉，为什么这么说呢？

（大屏幕上显示：东台市时堰中学、东台市实验中学）

师：大家一起将两个校名读一遍。

（生齐读）

师：哪位同学能发现其中的奥妙？

生1：“时堰”和“实验”读音相同。

师：对了！“时堰”和“实验”读音相同，用数学的眼光看，“时堰”和“实验”读音不仅相似，而且全等。难道这就是传说中的“缘分”？

（听课老师和学生均大笑，鼓掌）

师：我们刚刚学习了二次函数，请大家思考，在本学期所学的内容中，有哪个章节的内容和“二次函数”特别有“缘分”，联系较密切？

生（齐）：一元二次方程！

师：下面和大家一起来学习第6章第3节“二次函数与一元二次方程”。

思考：通过两校校名的读音相同，引出课题“二次函数与一元二次方程”，不仅能拉近师生之间的距离，激发学生学习的兴趣，还渗透了类比的数学思想，暗示着本节课探究的这两个“二次”之间也有着很深的渊源。从教学反馈看，达到了教者预设的效果。

二、合作交流，探索问题

教学片段1：教师提出一个很具体的问题，请大家一起探究。

探究一：求二次函数y=x2-2x-3的图像与x轴的公共点坐标。

师：请同学们画出二次函数y=x2-2x-3的图像，仔细观察抛物线与x轴的公共点情况，它与一元二次方程x2-2x-3的两个实数根之间有什么联系呢？

生2：令y=0，可得x2-2x-3=0，解得x1=-1，x2=3，所以二次函数y=x2-2x-3的图像与x轴的公共点坐标是（-1，0）和（3，0）。

经过各位学生在准备好的网格纸上的画图（如图1），得出结论：抛物线与x轴的公共点横坐标为-1、3，即为一元二次方程x2-2x-3=0的两个实数根。

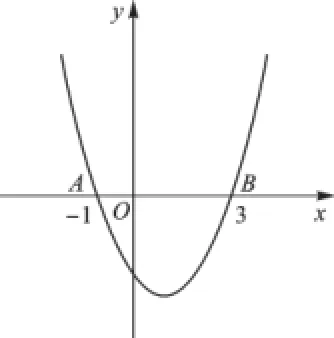
图1

思考：“探究一”从“函数值为0”着手，探索了二次函数与相应的一元二次方程之间的关系：①从函数关系式看，当二次函数y=x2-2x-3中的函数值y取特殊值0时即得到一元二次方程x2-2x-3=0；②从一元二次方程x2-2x-3=0的根的几何意义看，一元二次方程x2-2x-3=0的两实数根即为二次函数y=x2-2x-3的图像与x轴的公共点的横坐标，渗透了数形结合、从特殊到一般的数学思想方法，也体现了对立统一的辩证思想。

三、理性概括，构建新知

教学片段2：在教师指导下探究更一般的情形。

探究二：一元二次方程ax2+bx+c=0（a≠0）有两个不相等的实数根x1、x2，那么二次函数y= ax2+bx+c（a≠0）的图像与x轴有没有公共点？如果有，有几个公共点？说出公共点的坐标。

图2

生3：有两个公共点，坐标为A（x1，0）、B（x2，0）。

（注：如图2，教师适时地把图1中的A、B两点的横坐标换成图2中的x1和x2，让学生结合图形进行归纳，既能体现数形结合的数学思想方法，又能体会到从特殊到一般的思维方式）

思考：学生经历过“探究一”的特殊问题的探索，已经积累了一定的经验，归纳出一般性的结论已经水到渠成。通过“探究二”，可将重点放在引导学生体验从具体到抽象、从特殊到一般的思维方法上。

师：反过来，如果二次函数y=ax2+bx+c（a≠0）的图像与x轴有两个公共点A（x1，0）、B（x2，0），那么，一元二次方程ax2+bx+c（a≠0）的根的情况如何？

生4：有两个不相等的实数根x=x1、x=x2。

师：对，这就是说“如果二次函数y=ax2+bx+ c（a≠0）的图像与x轴有两个公共点A（x1，0）、B（x2，0），就等价于一元二次方程ax2+bx+c=0（a≠0）有两个不相等的实数根x1、x2”。而一元二次方程ax2+bx+c（a≠0）的根的情况又可以根据什么式子进行判断呢？

生5：根的判别式。

师：一元二次方程ax2+bx+c（a≠0）有两个不相等的实数根x1、x2，则根的判别式的符号如何？

生6：大于0。

师：正确，我们可以把它们之间的关系归纳如下表：

思考：把二次函数的图像与x轴有两个公共点、一元二次方程有两个不相等的实数根以及b2-4ac＞0三者关系由特殊到一般进行分析，最后归纳，大有瓜熟蒂落之感！并且三者之间关系紧密，用“等价于”符号相连接，体现了转化的数学思想方法。

四、实践应用，类比创新

师：经历了上述探究过程，我们已经基本学会了如何探索二次函数的图像与x轴公共点的情况、相应的一元二次方程根的情况以及这两者之间的关系。下面，请大家分组合作，完成探究，并把本小组讨论的最后结果归纳到数学探究报告单上．

数学探究报告单（一）

班级：_____姓名：_____组别：_____

日期：_______年___月___日

小组成员：_________组长：_________

评价成绩：_________

数学探究报告单（二）

班级：_____姓名：_____组别：_____

日期：_______年___月___日

小组成员：_________组长：_________

评价成绩：________________

思考：由于在“探究一”“探究二”中，学生已经学会了探究问题的方法，故后面的两个问题可以放手让学生分小组在合作过程中运用类比的方法继续进行探究，老师对有困难的小组适时进行引导、点拨，并以数学探究报告单的形式按“由特殊到一般”“类比”的数学思想方法进行归纳，然后以小组代表汇报的形式上台进行陈述，老师及时补充、小结、鼓励，使学生逐步获得技能。

五、归纳小结，提炼升华

教学片段3：师生共同总结涉及到的数学思想方法，并进行巩固练习。

师：同学们，经历了前面三组问题的探究，我们已经体会了哪些数学思想方法？

生7：数形结合。

生8：分类讨论。

生9：从特殊到一般。

生10：类比的思想。

师：这节课的课题是“二次函数与一元二次方程”，当然蕴含函数思想和方程思想。通过上面的探究，你能把我们刚刚得到的成果完整地归纳一下吗？

生11：抛物线与x轴的公共点个数和一元二次方程根的判别式Δ之间的关系（如图3）：

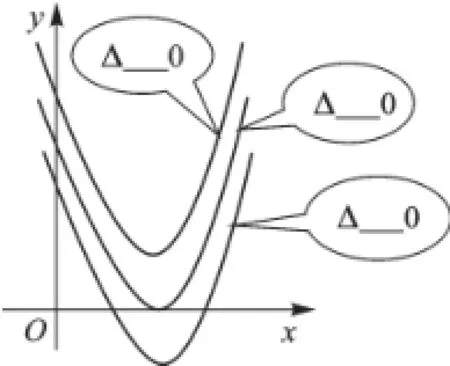
图3

（1）抛物线与x轴有两个公共点Δ>0；

（2）抛物线与x轴只有一个公共点Δ=0；

（3）抛物线与x轴没有公共点Δ<0。

（教师拿出一根粗电线做成的“抛物线”，配合生11，在黑板上进行抛物线的平移演示，主要目的是让学生进一步体会抛物线与x轴的公共点的个数，然后带着满脸的疑惑提问）

师：如果抛物线的开口方向向下呢？

生12：同样的只需要看其与x轴的公共点的个数，就能知道相应的一元二次方程的解的情况，也即知道根的判别式Δ与0的大小关系。

思考：让学生对照图形进行归纳，体现了数形结合的数学思想方法；平移“抛物线”，演示其与x轴的不同位置体现了分类讨论的数学思想方法；通过图3中的抛物线开口向上的情况进行归纳，然后提问开口向下时有何结论，体现了类比的数学思想方法。在这些方法的引领和渗透下，让学生把探究的过程、形成的结论进行归纳，学生的感受当然很“自然”。

师：同学们，课前大家欣赏的是什么歌曲？

生（齐）：《隐形的翅膀》。

师：大家会唱这首歌吗？

生（齐）：会唱。

师：今天这一节课我们运用了不少的数学思想方法来解决问题，这些数学思想方法就像“隐形的翅膀”，既能帮助我们解决问题，又能使我们的思维自由飞翔。老师将歌曲中的两句歌词改动了两个字。

（大屏幕上显示“我看见，每天的‘习题’也会有变化，我知道，我一直有双隐形的翅膀”，学生充满激情地齐唱）

师：大家唱得太好了！同学们，我们已经学得“本领”，应该到了大显身手的时刻了，让我们试试数学思想这个“隐形的翅膀”，怎样助你飞翔，请运用所学知识解决下列问题。

（1）不画图像，你能说出函数y=x2+x-6的图像与x轴的公共点坐标吗？

（2）判断下列函数的图像与x轴是否有公共点，并说明理由。

①y=x2-x；②y=x2+6x-9；③y=3x2+6x+11

（注：上面两道题是课本上的练习，目的是巩固二次函数与一元二次方程之间的关系，具体解法略）

（3）①已知抛物线y=x2+px-q与x轴的两个公共点为（-1，0）、（3，0），则p=____，q=_____；其对称轴为直线_________；②若x1和x2是一元二次方程ax2+bx+c=0（a≠0）的两个实数根，则抛物线y=ax2+bx+c（a≠0）的对称轴是_____________。

（4）已知抛物线y=x2-6x+a，①若其顶点在x轴上，则a=_________；②若与x轴有两个公共点，则a的范围是_________；③若与x轴没有公共点，则a的范围是_________；④将题目中抛物线y=x2-6x+a改为y=ax2-6x+1，则上面3个小题的答案有没有变化呢？

（5）已知：函数y=ax2+x+1的图像与x轴只有一个公共点，求这个函数关系式。（此题为盐城市2010年中考数学试卷最后一题的第1小题）

思考：上面两题主要考查学生对抛物线与x轴公共点的情况和一元二次方程根的判别式Δ之间的关系，渗透的是转化思想。值得一提的是第（4）题的第④小题，抛物线改为y=x2-6x+1后，需注意a≠0；尤其要注意的是第（5）题中的函数不一定是二次函数，它也可以是一次函数。两小题放在一起，让学生通过比较，加深印象。评讲第（4）（5）两小题时，还用了教者自编的防错“诀招”：“函数关于爱克斯（x），一次二次要三思！”此口诀通俗有趣，便于记忆，利于理解，深受听课师生的欢迎。

（6）二次函数y=x2-2x+m的图像与坐标轴有两个公共点，求m的值。

思考：解本题时学生极易在两处出错。首先，题目条件是已知“函数图像与有两个公共点”，学生容易错看成“与x轴有两个公共点”；其次，只考虑抛物线与x轴只有一个公共点（抛物线与x轴相切）的情形，遗漏了抛物线与x轴有两个公共点且经过原点的情形。解此题应分别考虑m=0和m≠0两种情况，本题渗透的是分类的数学思想方法。总而言之，教者精心设计的练习，旨在检测学生对两个“二次”关系的理解，体现数学思想方法的渗透和对学生完成练习的指引作用。