线上三等角笔下寻相似——对一道课本例题的拓展探究

季叶红

线上三等角笔下寻相似——对一道课本例题的拓展探究

季叶红

苏科版《数学》九（下）第56页例3：

已知，如图，在△ABC中，AB=AC，点D、E分别在BC、AB上，且∠BDE=∠CAD.△ADE与△ABD相似吗？为什么？

【分析】由等腰三角形的性质得出∠B=∠C，由三角形的外角性质和已知条件得出∠ADE=∠C，因此∠B=∠ADE，∠DAE=∠BAD，即可得出△ADE∽△ABD.

解：△ADE与△ABD相似.

∵∠ADB=∠C+∠CAD=∠BDE+∠ADE，

∠BDE=∠CAD，

∴∠ADE=∠C.

又∵AB=AC，∴∠B=∠C.

∴∠ADE=∠B.

∵∠DAE=∠BAD，

∴△ADE∽△ABD（两角分别相等的两个三角形相似）.

上述例题中，可知点B、D、C在同一直线上，且满足∠B=∠ADE=∠C，这样一个基本图形，我们称之为“K型图”，得△ACD∽△DBE.翻看全国各地中考数学试卷，以“K型图”为载体的中考试题频频出现，精彩纷呈.现归纳几种常见模型，供同学们学习时参考.

模型一

如图1，在Rt△ABC和Rt△CDE中，∠B=∠D=∠ACE=90°，点B、C、D在同一直线上，则△ABC∽△CDE.

图1

【分析】由∠BCE是△CDE外角，可知∠ACB+∠ACE=∠D+∠E，故可知∠ACB=∠E，根据两角分别相等的两个三角形相似，可知△ABC∽△CDE.

（1）直接应用：

如图2，正方形ABCD的边长为1cm，M、N分别是BC、CD上两个动点，且始终保持AM⊥MN.当BM=______cm时，四边形ABCN的面积最大.

图2

【分析】利用模型一，易证△ABM∽△MCN.

设BM=x，则CM=1-x，由相似三角形对应线段成比例得CN=x-x2，所以S四边形ABCN=x-x2），配方可得，当BM=时，面积最大.

（2）构造应用：

很多时候，题目中的图形并不是模型一直接出现的，但符合“K型图”特征，那么我们需要添加适当的辅助线构造出模型一中的基本图形.

图3

【分析】通过添加辅助线，构造模型一中的基本图形，易证△ACO∽△ODB，由相似图形的面积比等于相似比的平方，得

模型二

如图4，已知点B、C、D在同一直线上，且∠B=∠1=∠D，则△ABC∽△CDE，证明方法与相似模型一相同.

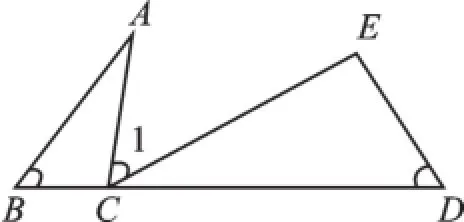
图4

直接应用：

如图5，△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α， DE交AC于点E，且cosα=.下列结论：

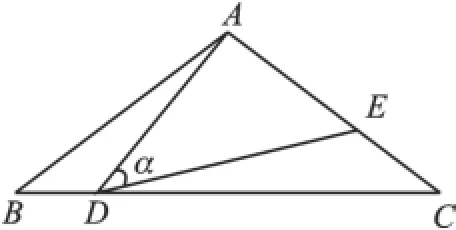
图5

①△ADE∽△ACD；②当BD=6时，△ABD与△DCE全等；③△DCE为直角三角形时，BD为8或；④0＜CE≤6.4.其中正确的结论

是________ .（把你认为正确结论的序号都填上）

【解析】利用模型二，易证△ABD∽△DCE，故可知正确答案为①②③④.

上述两种基本模型，可以简单归纳为：一线三等角，相似两三角（形）.实际解题时，若能把握图形本质，排除图形干扰，在复杂的图形中构造出“K型图”，写出图中的一对相似三角形，然后根据相似三角形的有关性质列出所需的比例式，则能化难为易，快速解题.

（作者单位：江苏省常熟市实验中学）

扫描二维码，观看名师微课