目标偏心误差与竖盘指标差对放样的影响分析
2016-12-07史晓涛王旭华
史晓涛,王旭华
(大连大学建筑工程学院,辽宁大连 116622)
目标偏心误差与竖盘指标差对放样的影响分析
史晓涛∗,王旭华
(大连大学建筑工程学院,辽宁大连 116622)
虽然3S技术已经广泛应用于测绘领域,但是基于全站仪的传统测量仍然有着不可替代的作用[1]。在利用全站仪放样时,其精放样阶段以水平角测量与距离测量两部分操作为主。通过分析对中杆偏心误差和竖盘指标差对水平角测量与距离测量的影响,定量地描述了其规律,对放样过程中的超差现象进一步做出合理的解释分析,提出高效的处理方法,对放样工作具有一定的指导意义。
放样;水平角测量;距离测量;对中杆偏心误差;竖盘指标差
1 引 言
虽然3S技术已经广泛应用于测绘领域,但是基于全站仪的传统测量仍然有着不可替代的作用[1]。在利用全站仪放样时,精放样阶段以测角与测距两部分操作为主。目前,对放样的误差研究主要是视准轴误差、横轴误差、竖轴误差、照准部偏心误差和对中误差。本文通过分析对中杆的偏心误差对测角的影响和全站仪竖盘指标差对单向与往返测距的影响,完善了仪器误差对放样误差影响的分析,对放样过程中的超差现象做出进一步合理的解释分析,提出高效的处理方法,减小误差,提高效率,为是否需要检修仪器提供了依据。
2 对中杆偏心误差对放样的影响及处理方法
2.1误差分析
对中杆偏心误差属于测量学中的目标偏心误差范畴,是指照准点上所竖立的目标与地面点的标志中心不在同一铅垂线上引起的水平方向观测误差,其对水平方向观测的影响如图1所示。

图1 目标偏心误差对水平角观测的影响
设B点为测站点,A为照准点标志中心,A′为实际瞄准的目标中心,D为两点间的距离,e为目标的偏心距,θ为e与观测方向的水平夹角,则目标偏心误差对水平方向观测的影响为[2]:

由式(1)可知,当θ=90°时,γ″取得最大值。即与瞄准方向垂直的目标偏心对水平方向观测影响最大。
对中杆偏心误差是由于圆水准器的中心轴与杆的中心轴不平行,导致圆水准气泡居中时反光镜的中心与地面标志中心不在同一铅垂线上,不仅对测角有较大影响,对测距也会产生较大误差。如图2所示,设放样区域为一个矩形,A为测站点,则测角总误差为:

图2 放样区域示意图

考虑到δ1与δ2较小,则有:

当θ=90°时,δ取得最大值:

当θ1和θ2达到0°或180°时,对测距的影响最大,△Dmax即为目标偏心距e1与e2的值。
综上所述,对中杆偏心误差对放样有较大影响,在超过一定限度时必须进行校正。
2.2处理方法
由于对中杆偏心误差对测量结果的影响较大,测绘工作开始前,应对对中杆进行严格的校检,以保证圆水准气泡居中时,对中杆竖直。常用的对中杆分为单对中杆和三脚对中杆,因三脚对中杆的放样结果更加精确,本文仅讨论三脚对中杆的检验校正。可采用“两方向相交法(第一种方法)”与“单方向交叉法(第二种方法)”进行检验校正[3]。
第一种方法如图3所示,将全站仪安置在O点,使OA、OB两线呈90°夹角,在O点安置对中杆,从A方向用全站仪观测,保持照准部水平不动,仅上仰望远镜使水平丝平分棱镜,操作对中杆仅伸缩BO方向上的支脚,使望远镜竖丝正好平分棱镜,这时对中杆在AO方向竖直。同理,可以使杆在BO方向垂直。这时调整圆水准气泡居中即可。

图3 两方向相交法
第二种方法如图4所示,将三脚对中杆立于O点,在A点安置全站仪并瞄准O点处对中杆的下尖,保持全站仪照准部水平不动,仅上仰望远镜使水平丝平分棱镜,操作对中杆伸缩OE方向上的支脚,使望远镜竖丝恰好平分棱镜,这时对中杆在AO方向竖直,调整圆水准器使气泡居中。保持对中杆的下尖不动,将两支脚一起转动90°,使一支脚移至OF方向线上,另一支脚移至AO延长线上,按照上一步方法继续校正,直到对中杆竖直时气泡居中。

图4 单方向交叉法
3 全站仪竖盘指标差对放样的影响
竖盘指标差是指竖盘指标水准器与竖盘读数指标关系不正确时,望远镜视准轴水平时的竖盘读数相对于正确值90°(盘左)或270°(盘右)的角度偏差x。而全站仪测距的原理是根据所测斜距SD通过竖直角α转化为平距,因此,当放样区域存在坡度时,竖盘指标差就会对测距产生影响。
3.1盘左观测时的测距误差分析
设竖直角理论值为α,斜距理论值为SD,设平距的测量值为HDL,理论值为HD理,误差为△HDL,竖直角的观测为αL。则根据三角测量原理,可得:

由式(6)和式(7)可得:

由式(8)可以看出,平距的误差同SD、α与x三个变量都相关。因此本文利用相对误差,用△HDL与HD理的比值进行误差程度分析,消除SD1的影响。

由式(8)可知,相对误差只与α和x有关且与α的大小成负相关。将1°~60°的竖直角与1″~4′15″的竖盘指标差一一对应代入式(8)进行计算,部分数据如表1所示。根据规范,全站仪竖盘指标差超过1′就需要校正,放样的相对误差允许在1/5000范围内合格[5]。根据计算结果,当竖盘指标差为1′时,竖直角达到34°,相对误差就会达到1/5000,因此竖盘指标差保持在1′的范围内并不能保证测距相对误差不超限。而竖直角为10°时,竖盘指标差超过3′49″才会导致相对误差超限,所以在竖直角不超过10°且指标差在3′49″之内,都不会因此导致测距误差超限。
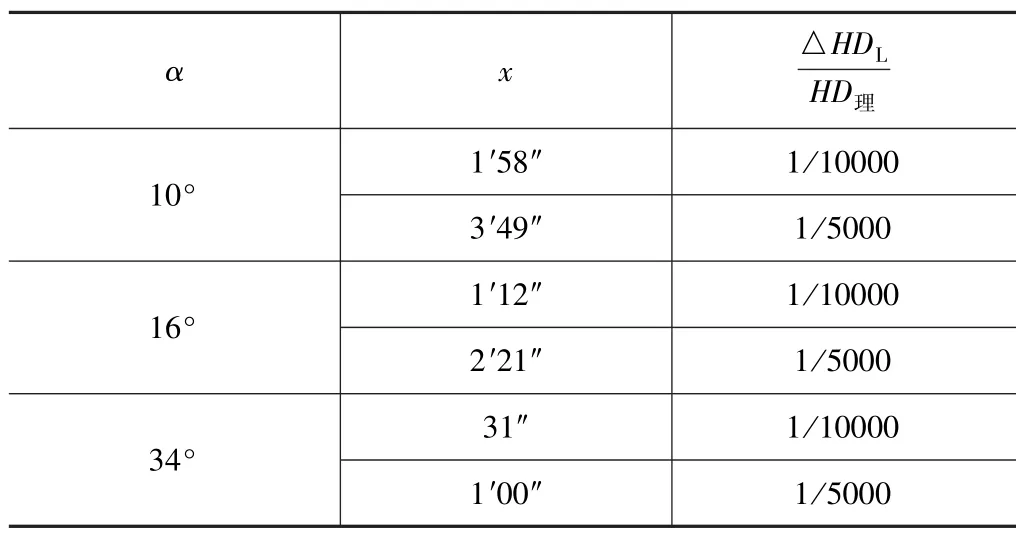
盘左观测时的测距相对误差部分数据 表1
3.2盘右观测时的测距误差分析
盘右观测的误差程度分析原理与盘左观测相似。设平距的测量值为HDR,误差为△HDR,盘右的观测竖直角为αR。则根据三角高程原理,可得:

由式(11)可知,盘右观测时,相对误差与x和α的大小均成正相关。用同样的计算方法,得出的部分数据见表2。根据计算结果,当竖盘指标差为1′时,竖直角达到35°,相对误差就会达到1/5000,因此竖盘指标差保持在1′的范围内并不能保证测距相对误差不超限。而竖直角为10°时,竖盘指标差超过3′53″才会导致相对误差超限,所以在竖直角不超过10°且指标差在3′53″之内,都不会因此导致测距误差超限。

盘右观测时的测距相对误差部分数据 表2
3.3盘左盘右观测取平均值的测距误差分析
由于盘左盘右观测取平均值可以消除竖盘指标差的影响,本文通过分析盘左盘右分别测距取平均值的误差程度,判断该方法是否能减少误差及减少误差的程度。设测距的平均值为误差为△HD。

由式(14)可知,双盘位测距取平均值的相对误差只与x有关且误差与x的大小成正相关,其值介于0和1之间。将1″到4′15″的竖盘指标差分别代入式(14)进行计算,部分数据如表3所示。
由表3可以看出,即使竖盘指标差达到10′,测距的相对误差仍然在允许误差范围之内。双盘位观测取平均值对测距精度有了极大的提高。

双盘位观测时的测距相对误差部分数据 表3
4 结 论
(1)对中杆偏心误差既会影响测角又会影响测距,偏心距与观测方向的水平夹角θ达到90°时对测角影响最大,达到0°或180°对测距影响最大。且对中杆偏心误差的数量级大于竖盘指标差,因此误差超限时首先考虑对中杆偏心误差的影响,及时进行校正。
(2)在遵循规范中“全站仪竖盘指标差不超过1′”的要求时,因竖直角的影响,并不能保证测距相对误差不超限。仅盘左或盘右测距时,满足竖直角在34°以内的条件下,竖盘指标差不超过1′方可保证误差不超限。因此,为避免误差超限,宜选择盘左盘右分别测距取平均值的测距方法。
[1] 杨靖英,程相兵.基于智能全站仪外业数据采集系统的设计与实现[J].城市勘测,2011(4):132~134.
[2] 覃辉,伍鑫.土木工程测量(第4版)[M].上海:上海同济大学出版社,2013:68~70.
[3] 郑平元,杨武年,余代俊.测量对中杆检校的实用方法探讨[J].城市勘测,2011(4):147~148.
[4] 郭旭.三角高程代替几何水准的可行性[J].城市勘测, 2014(4):109~112.
[5] GB 50026-2007.工程测量规范[S].
The Analysis about Error of Target Eccentricity and Index Error of Vertical Circle for Layout Survey
Shi Xiaotao,Wang Xuhua
(College of Civil and Architectural Engineering,Dalian University,Dalian 116622,China)
Traditional civil engineering measurement based on the total station is still irreplaceable,although 3S technology is widely used in the field of surveying and mapping.Horizontal angle survey and distance measurement are operated mainly in the stage of the pure layout when the total station is used in the layout survey.According to the analysis of the influence in the horizontal angle survey and distance measurement,which is created by the error of target eccentricity and the index error of vertical circle,the rules are described quantitatively,the reasonable analysis and explains about the overproof phenomenon are further given,the efficient solutions are put forward and the solutions will have a certain guiding significance in the layout survey.
layout survey;horizontal angle survey;distance measurement;error of target eccentricity;index error of vertical circle
1672-8262(2016)01-138-04
P204
B
∗2015—12—10
史晓涛(1995—),男,研究方向:岩土与基础工程及工程测量。
王旭华(1963—),男,博士,教授,研究方向:工程测量教学和边坡观测及分析。
国家自然科学基金(51274051)
