基于EGM2008和多面函数的太原市似大地水准面精化
2016-12-07刘瑛张德明
刘瑛,张德明
(太原市勘察测绘研究院,山西太原 030002)
基于EGM2008和多面函数的太原市似大地水准面精化
刘瑛∗,张德明
(太原市勘察测绘研究院,山西太原 030002)
采用EGM2008重力场模型和趋势面拟合与基于正交最小二乘思想筛选节点的多面函数法,运用移去恢复原理建立了太原市区的似大地水准面模型,拟合得到的模型内符合与外符合中误差均小于2 cm,完全可以满足太原市区内常规测量的要求。
EGM2008;趋势面拟合;多面函数;似大地水准面
1 引 言
建立一个区域的似大地水准面模型,比较标准的方法是移去恢复法,即将测区范围内离散的点进行GPS水准联测后,把求出采样点的高程异常分解成中长波分量、短波分量和残余部分[1]。此时用模型大地水准面来表示中长波部分,用足够分辨率的数字地形模型计算短波部分,以上两部分可认为是趋势项,在计算时先移去此部分。再对残余部分用数学或统计的方法,如多项式、多面函数、最小二乘配置等方式进行拟合。最后再将拟合结果和趋势向相叠加,恢复最初的高程异常进而拟合出该区域的似大地水准面模型。
通常趋势项部分由重力场模型计算求出,在精化似大地水准面方面,许多学者对各个重力模型进行了对比,均显示EGM2008模型精度要优于其他模型,并肯定了其在中国大陆地区的适用性。因此在进行似大地水准面精化时,EGM2008是计算模型大地水准面的首选地球重力场模型[2]。
在对残余部分进行拟合时,采用多面函数是比较普遍的做法。为了突出反映高程异常的变化,在进行多面函数拟合之前,可先进行趋势面分析,再对剩余部分进行曲面拟合;而在多面函数拟合中,节点的选择对最终的结果影响较大,因此本文采用正交最小二乘的思想来筛选节点[3]。
2 基于EGM2008重力场模型和趋势面正交多面函数的移去恢复法基本思想
高程异常ζ可分为长波分量、短波分量和残余部分,即:

长波分量ζGM可由重力场模型求出[4],短波分量ζT通过数字高程模型计算[4],移去的过程即求出残余部分的高程异常:

如果没有数字高程模型,也可以将短波部归入残余高程异常:

由于重力场模型、GPS大地高、水准高均存在测量误差、重力模型高频分量以及不同基准面等的影响,模型大地水准面和实测水准面之间还会存在系统性偏差[5,6]。而从拟合的角度来说,残余的高程异常仍可认为由趋势项和随机信号两部分组成,因此可先对趋势面进行分析,再对剩余部分进行拟合操作。将高程异常的趋势面表示为与坐标的函数:

式中f(x,y)常为多项式函数,可由最小二乘法求出系数。判断最终拟合的结果是否显著,可进行F检验[7]。如果存在异常的观测值,则需采用抗差估计来控制其对参数求解的影响[3,8]。
在经过趋势面分析之后,采用多面函数进行最终的拟合,多面函数可将某一点的高程异常ζ(x,y)表示为:
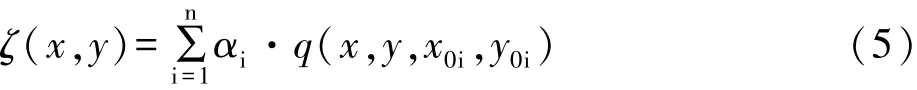
式中,αi为待求参数,n为参数个数,q为核函数。
拟合的关键就是核函数的确定,这其中又以节点的确定最为关键,可从观测点中选择均匀分布的点作为结点,但此种做法带有一定的随机性。为了能用最少的参数逼近到满足要求的精度,通常需要对节点进行筛选,可通过显著性t检验[9]、逐步回归[10]以及正交最小二乘的方式[3,11]进行选择。
采用正交最小二乘的方式来筛选,若将所有观测点作为节点,并表示成列向量的形式,误差方程的系数矩阵可表示为:

式中,βi=[q(x1,y1,x0i,y0i) q(x2,y2,x0i,y0i)… q(xn,yn,x0i,y0i)]T,将βi相互正交化,则观测向量Z和βi的夹角θ为:

θ值越大,则对应的βi,即参数αi对应的节点对拟合的贡献越大。因此,可以通过判断正交化的系数矩阵与观测值夹角大小的方式来筛选结点,从而以较少的参数达到较高的拟合度,同时又能有足够的多余观测来保证推估的可靠性。
3 太原市区似大地水准面精化案例分析
3.1概况
为了满足太原市城市建设和规划发展及现代化测绘生产的需要,本文利用了太原市区的控制测量成果和EGM2008重力场模型对市区的高程异常进行了拟合。控制点均为E级GPS点,共194个,较为均匀地分布在了太原市建成区及清徐县的平坦地区。所有点位均联测了二等水准,获得了在WGS84坐标系下的大地高以及在太原高程基准大沽高程系下的正常高。求得了这些点的高程异常值采用MATLAB双调和样条插值内插出的高程异常等值线如图1。从194个点中,选择146个点进行拟合计算,其余48个点作为检查点用于外部质量评价,点位分布如图2所示。
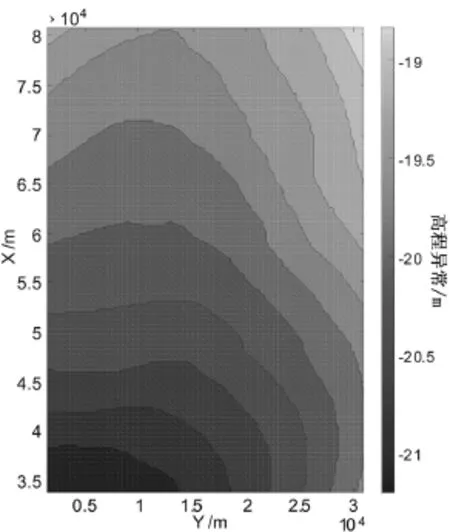
图1 高程异常等值线
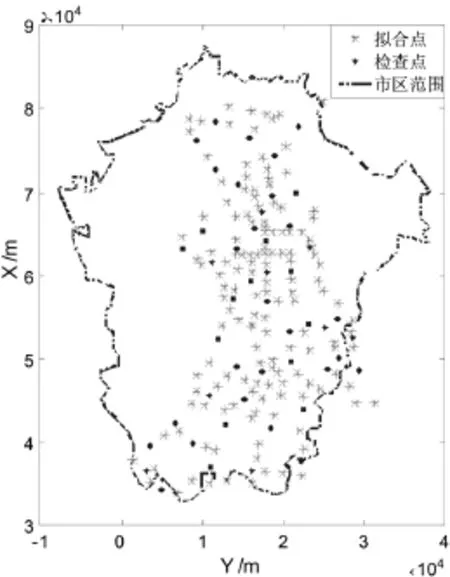
图2 拟合点与检查点分布
3.2模型高程异常的移去
本文利用1′×1′的EGM2008模型文件计算出了太原市区的格网模型高程异常,如图3所示。
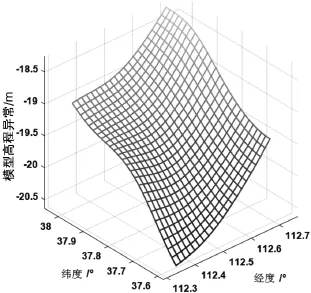
图3 EGM2008下的太原市区高程异常
同时根据控制点的经纬度计算了各个点位的模型高程异常,并通过GPS水准获取的高程异常求出了残余高程异常。从图1和图3可以看出,通过控制点的高程异常绘制的等值线和模型高程异常值均呈现由东北向西南减小的趋势的各控制点残余高程异常如图4所示。3.3 趋势面及多面函数拟合
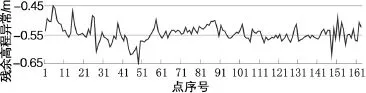
图4 残余高程异常值
扣除模型高程异常后的残余高程异常ζ仍有系统性偏差,本文采用四参数模型[5]进行趋势面拟合:
ζRES=a0+a1cosφcosλ+a2cosφsinλ+a3sinφ+v(8)
拟合过后再对残余的高程异常进行多面函数拟合。首先基于正交最小二乘筛选节点,将所有的146个高程异常点作为节点插值的情况求出系数矩阵并进行Gram-Schmidt正交化,再根据式(7)求出各个参数的对应系数矩阵向量与高程异常向量的夹角,从中筛选出39个点作为节点。再通过简单试算确定曲面类型和平滑因子,即可确定核函数,并求出每个节点对应的参数。测区范围内扣除模型高程异常的残余部分经过趋势面和多面函数拟合之后的结果如图5所示。
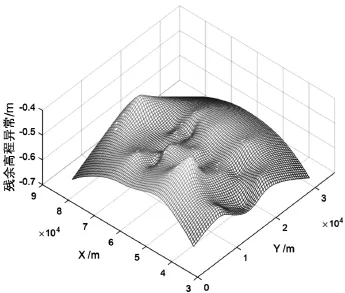
图5 残余高程异常拟合结果
3.4结果及精度评定
将各控制点的高程异常移去模型高程异常并拟合出残余高程异常的参数后,太原市区的任意一点高程异常值即可通过简单的恢复过程求出,拟合的最终结果如图6所示。
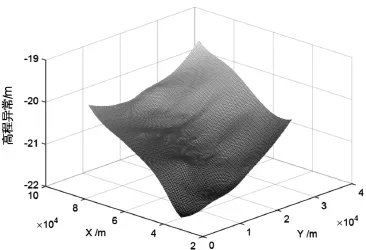
图6 最终拟合结果
参与计算的146个控制点拟合残差以及48个检查点的不符值如图7、图8所示。
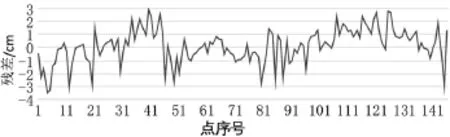
图7 拟合残差
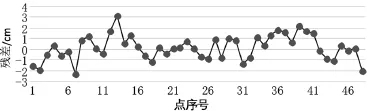
图8 检查点残差
最终的统计结果如表1所示。

拟合结果统计 表1
从图7、图8、表1看出,采用EGM2008重力场模型以及趋势面和多面函数进行拟合的结果,除一个点的残差为3.51 cm外,其余拟合残差均小于3 cm,内符合精度为1.62 cm;外符合精度的最大不符值为3.14 cm,其余结果均小于2.5 cm,外符合精度为1.13 cm,总体上有着较好的拟合精度。
4 结 论
本文利用移去恢复原理,将高程异常分成模型高程异常,残余高程异常的趋势项部分和残余高程异常的信号部分,分别利用EGM2008重力场模型、趋势面拟合和正交多面函数法建立了太原市区的似大地水准面模型。最终结果的内符合精度为1.6 cm,外符合精度为1.1 cm,该拟合模型可以满足太原市区常规的测绘生产需求。
[1] 宁津生,罗志才,杨沾吉等.深圳市1Km高分辨率厘米级高精度大地水准面的确定[J].测绘学报,2003,32(2): 102~107.
[2] 刘东顺.基于EGM2008的似大地水准面精化方法研究[D].沈阳:东北大学,2010.
[3] 张菊清,刘平芝.抗差趋势面与正交多面函数结合拟合DEM数据[J].测绘学报,2008(4):526~530.
[4] GB/T 23709-2009.区域似大地水准面精化基本技术规定[S].
[5] 肖杰,张锦,邓增兵等.矿区似大地水准面精化方法研究[J].测绘通报,2015(2):14~18.
[6] 荣敏,周巍,陈春旺.重力场模型EGM2008和EGM96在中国地区的比较与评价[J].大地测量与地球动力学, 2009,29(6):123~125.
[7] 刘大杰,陶本藻.实用测量数据处理方法[M].北京:测绘出版社,2000.
[8] 赵丽华.区域地壳运动模型实现的理论与方法研究[D].西安:长安大学,2011.
[9] 陶本藻,余井泉.变形模型运动参数的筛选和运算[J].测绘学报,1988(4):241~246.
[10] 赵承坤,黄立人.速率面拟合法中核函数中心点的选择[J].地壳形变与地震,1991(2):48~54.
[11] S Chen,CN Cowan,PM Grant.Orthogonal Least Squares Learning Algorithms for Radial Basis Function Networks[J].IEEE Trans Neural Networks,1991,2(2):302~309.
[12] 黄立人,陶本藻,赵承坤.多面函数拟合在地壳垂直运动研究中的应用[J].测绘学报,1993(1):25~32.
Taiyuan Quasi-Geoid Refinement Based on EGM2008 and Multi-Surface Function
Liu Ying,Zhang Deming
(Taiyuan Institute of Surveying and Mapping,Taiyuan 030002,China)
A quasi-geoid model in Taiyuan urban areas established by using remove-restore method based on EGM2008 gravity field model,trend surface fitting and multi-surface function which choosing nodes by using the orthogonal least squares.The result shows that root mean square error of internal and external quality evaluation are both less than 2 cm,completely meet the conventional surveying production demand in the urban area of Taiyuan.
EGM2008;trend surface fitting;multi-surface function;quasi-geoid model
1672-8262(2016)01-20-04
P223
B
∗2015—10—09
刘瑛(1979—),男,工程师,主要从事工程测量和测量项目管理工作。
