深海热液硫化物矿体3D瞬变电磁正演

李瑞雪， 王鹤， 席振铢*， 龙霞,2， 侯海涛,2， 刘愿愿， 蒋欢

1 中南大学 地球科学与信息物理学院， 长沙 410083 2 湖南五维地质科技有限公司， 长沙 410025



深海热液硫化物矿体3D瞬变电磁正演

李瑞雪1， 王鹤1， 席振铢1*， 龙霞1,2， 侯海涛1,2， 刘愿愿1， 蒋欢1

1 中南大学 地球科学与信息物理学院， 长沙 410083 2 湖南五维地质科技有限公司， 长沙 410025

深海热液硫化物矿体瞬变电磁的正演是考虑深海环境的全空间条件下三维体的涡流电磁响应.采用全空间矢量有限元法模拟计算深海热液硫化物矿的三维瞬变电磁响应，对硫化物矿体采用矩形单元模型剖分，应用Galerkin法推导有限元方程，先计算频率域响应，再通过Fourier反变换将其转换至时间域，得出深海热液硫化物矿矿体的瞬变电磁响应.并用双半空间模型的解析解检验了全空间矢量有限元法模拟计算算法和程序的正确性，最后按照等比例缩小电磁物理实验原则，比对数值计算和物理实验结果论证了全空间3D模型数值的正确性.结果表明：对于海水、矿体以及围岩复杂电磁边界，应用全空间矢量有限元法模拟计算深海热液硫化物矿瞬变电磁响应异常与物理模拟结果一致，而且计算方法简单精确，异常幅值明显，边界清晰.

深海热液硫化物矿； 矢量有限元； 海洋瞬变电磁法； 全空间3D正演

1 引言

深海热液硫化物矿广泛分布于大洋扩张脊、弧后扩张中心以及热点火山构造带内，其经济价值在近几十年内被深刻认识.目前已知的典型硫化物矿热液区范围巨大，分布着储量可观的硫化物丘体和硫化物矿堆积体，矿藏丰富(邓希光, 2007; Богданов, 2007).当前，日益减少的陆地金属矿产资源以及迅速增长的金属资源需求推动着深海热液硫化物矿探测的发展，如何在热液区内探测深海热液硫化物矿床成为重要问题.

近年来，应用于深海矿产勘察的海洋瞬变电磁法受到广泛关注(Cheesman et al., 1990; Yu et al., 1997; Danielsen et al., 2003; Börner et al., 2015; Swidinsky et al., 2015).深海热液硫化物矿的瞬变电磁响应特征是应用该方法探矿的基础，已有学者对其做了研究.Cheesman 等(1987)计算了海洋双半空间模型多种装置的瞬变电磁响应，刘长胜和林君(2006)通过海洋层状模型的频率域响应表达式推导了中心回线装置和重叠回线装置的瞬变电磁响应表达式，Swidinsky等(2012)在上述研究基础上计算了深海洋底导电层的中心回线装置及重叠回线装置瞬变电磁响应；周胜等(2012)运用全空间理论计算方法模拟了深海热液硫化物矿床层状模型重叠回线装置瞬变电磁响应；胡俊华等(2013)采用余弦变换多项式近似法对海洋层状模型的中心回线装置瞬变电磁响应进行了一维正演计算.Jang 和Kim(2015)进行了中心回线瞬变电磁法探测深海热液矿床的一维正反演研究.以上模拟计算，把海底硫化物矿体简化为层状模型.然而， Evans和Everett(1994), Богданов(2007),Swidinsky等(2012)分别对Galapagos洋脊热液矿化堆，大洋低速扩张脊热液成矿系统，俾斯麦海块状硫化物矿堆的研究表明，深海地球物理环境以洋底面为界分为海水与玄武岩基底两个半空间，硫化物在洋底面堆积成矿，洋底面以下为热液喷出通道及蚀变带，硫化物矿体整体呈锥形或透镜状，是全空间中的三维体，席振铢等(2016)通过分析研究大西洋洋中脊以及西南印度洋洋中脊热液硫化物矿实测数据将其简化为三维目标体.因而，采用三维正演计算是模拟深海热液硫化物矿瞬变电磁响应的有效手段.

为提高计算速度，增强计算实用性，本文将深海热液硫化物矿简化为低阻长方体进行三维数值模拟，应用全空间矢量有限元法计算其瞬变电磁响应.首先，通过双半空间模型的计算验证全空间矢量有限元法的正确性；其次，建立深海热液硫化物矿的三维电性模型，应用全空间矢量有限元法计算其瞬变电磁响应，总结响应特征；最后，通过物理实验验证深海热液硫化物矿瞬变电磁响应数值模拟结果的正确性.

2 计算方法

如图1所示，深海硫化物矿体、海水和围岩的电磁边界复杂，Γin是海水与洋底的界面，Γa是热液硫化物矿的外边界，Γout是计算区域外边界.在这些边界上，电场的法向分量不连续，切向连续.传统的节点有限元计算方法需要所有场分量连续，因而不能获得精确解.不同于节点有限元法，矢量有限元法将场分量作为整体进行插值求得更精确的解(Jin, 2002; Sugeng, 1998; Cai et al., 2014; 黄威等, 2016).

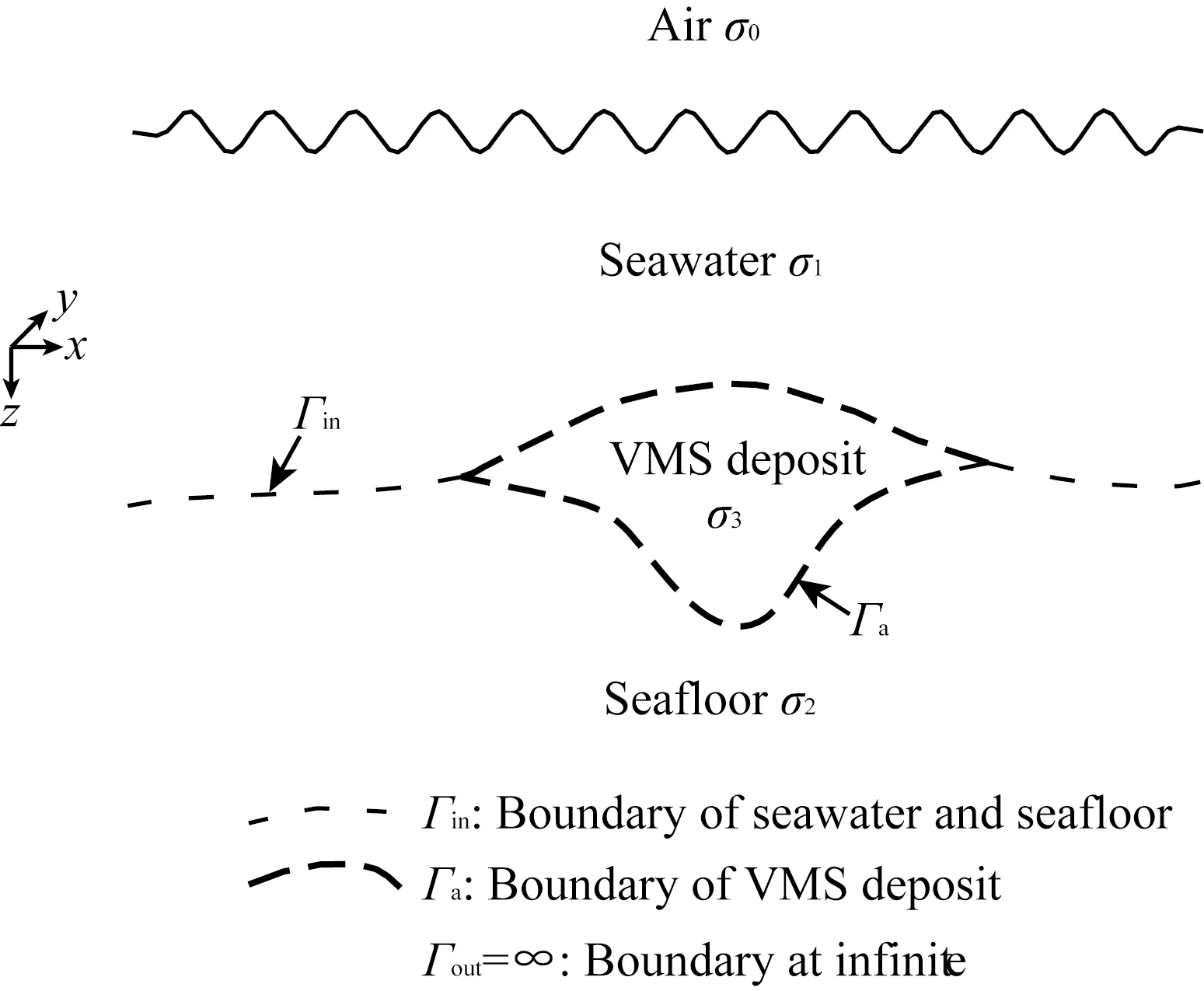
图1 计算区域不考虑σ0, σ1=3 S·m-1, σ2=0.01-100 S·m-1, σ3=10 S·m-1Fig.1 Computational domainσ0 is not considered, σ1=3 S·m-1, σ2=0.01-100 S·m-1, σ3=10 S·m-1

2.1 边值问题

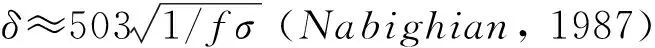
电磁场可通过解麦克斯韦方程组求得，取时间因子eiω t，全空间的麦克斯韦方程为

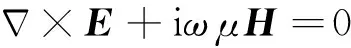
(1)

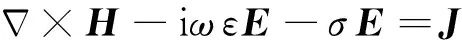
(2)

其中,E是电场，H为磁场，ω为角频率，μ为磁导率，ε为介电常数，σ为电导率，J为源电流密度.对公式(1)取旋度，利用公式(2)消去磁场H，得电场的矢量波动方程：

(3)

上式中的电场是包含一次场和二次场的总场，总场的直接求解需考虑场源的空间奇异性，为模拟场源附近电场的快速变化，对模型进行剖分时须在场源附近做网格细化，导致待求量的增加.为解决上述问题，本文求解二次电场.将上式中的电场E分解：

E=Ep+Es,

(4)

式中，Ep表示一次电场，Es表示二次电场，则电场矢量波动方程可分解为

(5)

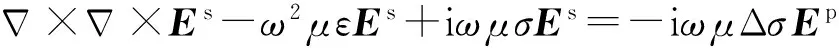
(6)

式中，Δσ表示电导率异常，是异常体电导率与背景电导率的差值.对于一次电场Ep，计算其在两个半空间背景模型中的解析解.将本文要模拟的重叠回线装置发射线圈分成多段作电偶极源考虑，计算每段电偶极源TE极化模式的电场(Nabighian, 1987)，并沿线圈积分求得一次电场.

深海环境下，海水电导率为3 S·m-1，玄武岩电导率取0.01 S·m-1，热液金属硫化物矿电导率取10 S·m-1，本文采用0.1～105Hz的频域响应进行时频转换，以上参数取值范围内，ω2μ ε≪ω μ σ，因此忽略位移电流做准静态近似，待求解的二次电场矢量波动方程简化为扩散方程：

(7)

如图1所示的计算区域，无穷远边界Γout上二次电场衰减为0，满足齐次狄利克雷边界条件：

Es=0,

(8)

内部介质分界面Γin及异常体界面Γa上，电场切向分量相等：

(9)

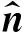
2.2 矢量有限元分析

本文采用的矩形单元如图2所示，图中数字表示棱边局部编号.

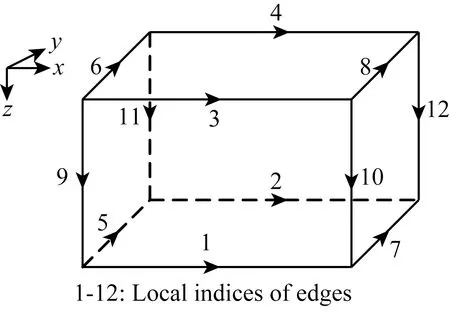
图2 矩形单元Fig.2 Rectangular brick element

根据矩形单元矢量基函数表达式(Jin, 2002) ，单元内的二次电场可由矢量基函数表示为

(10)

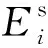
(11)

因此对于公式(10)表示的二次电场有

(12)

上式证明矢量基函数表示的电场自然满足零散度条件，从而保证求解结果二次可微，避免非物理解的出现.由公式(7)表示的二次电场扩散方程的残数为：

(13)

将单元内二次电场表达式(10)代入公式(13)并应用伽辽金方法(Jin，2002)可得单元内残数Re，其矩阵形式为

Re=[Ae]{Es}+[Be]{Es}+[Ce]{Ep},

(14)

其中[Ae]，[Be]，[Ce]为12×12阶单元矩阵：

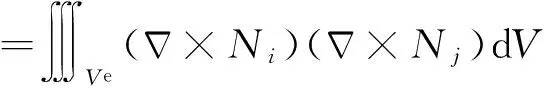
(15)

[Be]=∭Veiω μ σNiNjdV,

(16)

[Ce]=∭Veiω μΔσNiNjdV,

(17)

对所有单元组合单元方程(14)式，令与每一棱边相关的残数加权积分为0，得方程组：

Ke=-b,

(18)

其中，K为N×N阶整体矩阵，e、b为N阶向量，N是剖分模型总棱边数.

对于位于外边界上的棱边，其全局编码为n，令

bn=0,

(19)

(20)

实现狄利克雷条件的强加.由于矢量基函数Ni只在第i边上有切向分量，因此由式(10)表示的二次电场既保证了在棱边上的切向连续性，也保证了在单元界面上的切向连续性.

采用共轭梯度法求解方程组(18)得二次电场，二次磁场通过对式(10)应用法拉第定律求得：

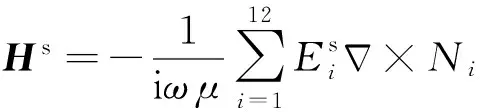
(21)

以上求解出频率域内二次磁场Hs，对其进行Fourier反变换求得二次磁场时间域响应(考夫曼等,1987).

3 模型计算

首先通过与Swidinsky双半空间模型计算结果进行对比验证程序正确性，然后将深海热液硫化物矿简化为双半空间中的低阻长方体，研究其瞬变电磁响应特征.本文计算均在CPU为2.5 GHz，RAM为4GB的个人计算机上完成.

3.1 双半空间模型

图3为Swidinsky双半空间模型，海水电导率取3 S·m-1，洋底半空间电导率分别取1、3 S·m-1、10、30 S·m-1和100 S·m-1.

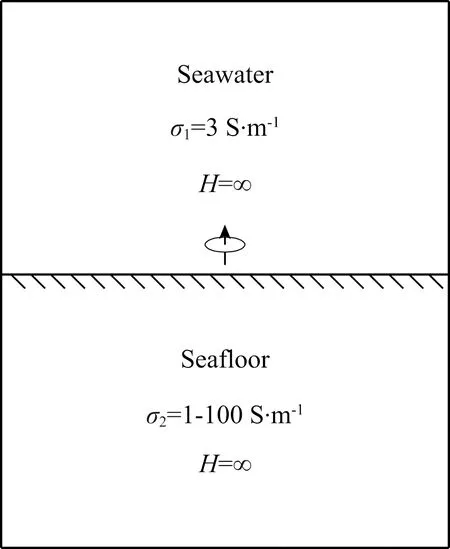
图3 双半空间模型海水及洋底厚度H为无穷大Fig.3 Double half-space model H-the depth of seawater and seafloor which is infinite

模型中没有地形起伏和复杂结构地质体，采用易于实现的矩形单元对模型进行剖分.剖分网格在海水-洋底界面处加密，剖分后各方向节点数21×21×14，总节点数6174，总棱边数17493，总单元数5200.洋底半空间电导率不同取值情况下计算时间分别为1459.89、970.81、665.69、279.88、211.25 s.图4为双半空间模型的归一化磁场衰减曲线以及误差图，其中符号为本文计算结果，线条为Swidinsky计算结果，二者吻合良好，最大误差2.97%，平均误差0.31%，说明本文算法正确.

3.2 三维模型

将深海热液硫化物矿简化为位于洋底面上的低阻方形板状体，并将海水及洋底视为均匀半空间，建立如图5所示的三维电性模型，海水电导率取3 S·m-1，玄武岩电导率取0.01 S·m-1，热液硫化物矿电导率取10 S·m-1.图5所示的深海热液硫化物矿三维电性模型异常体结构规则，采用矩形单元对模型进行剖分，剖分网格在异常体边界及洋底面处加密，图6为网格剖分示意图，红色区域为异常体，东西走向及南北走向延伸200 m，厚度50 m，计算区域2000 m×2000 m×2000 m，剖分后各方向节点数47×47×46，总节点数101614，总棱边数298309，总单元数95220.发射线圈及接收线圈采用10 m×10 m的方形回线，激发电流10 A，上升沿0.2 ms，持续时间400 ms，关断时间为0.2 ms.测线沿东西方向，线距50 m，共9条测线，每条测线9个测点，点距50 m，主测线中心测点位于异常体中心，共计81个测点，总计算耗时263586.15 s，平均耗时3254.15 s.

图7是主测线瞬变电磁响应多道剖面图，为直观地分析深海热液硫化物矿的瞬变电磁响应特征，取81个测点不同时间道的响应值绘制3D瞬变电磁响应图，如图8所示.

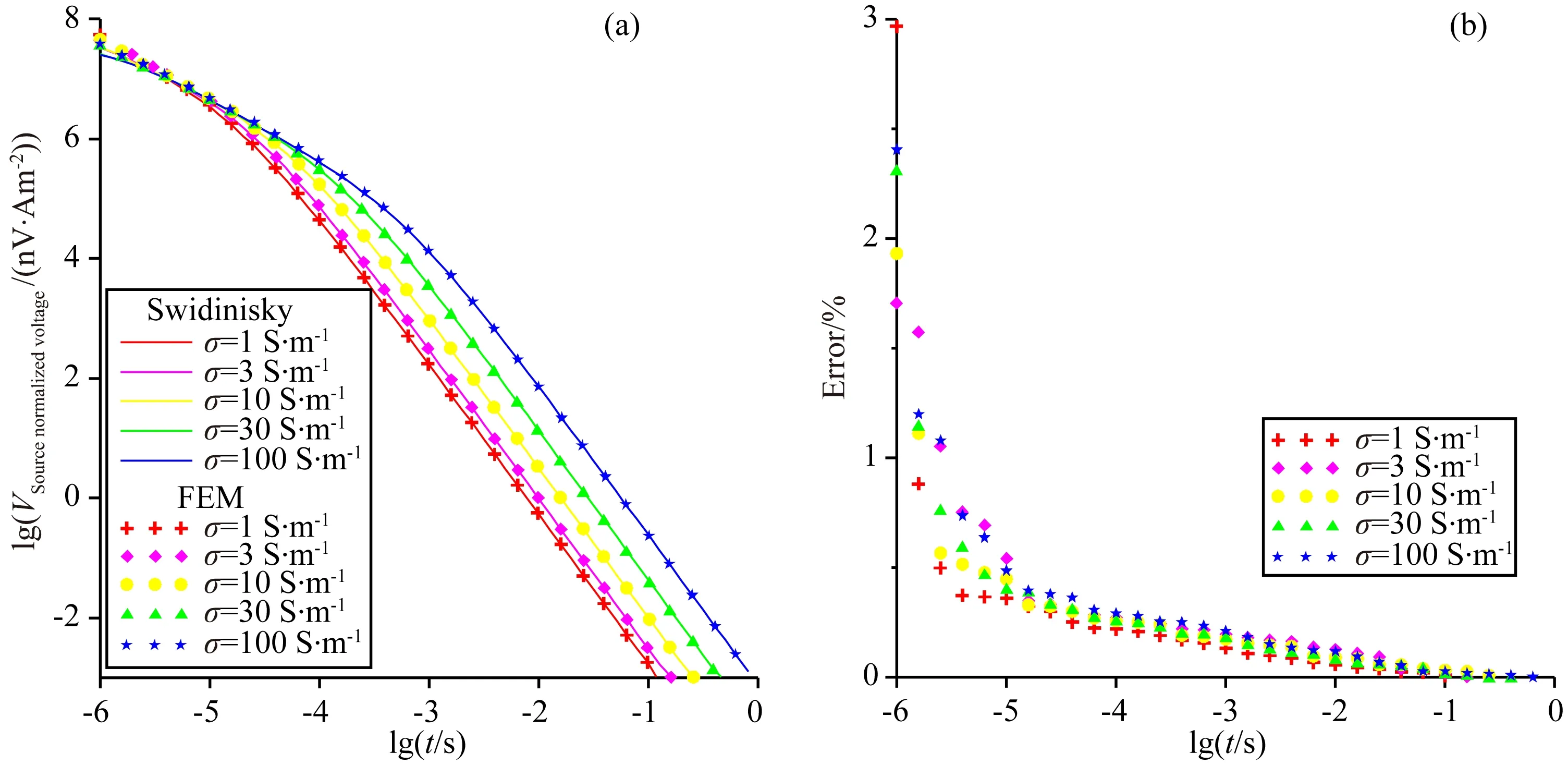
图4 双半空间模型瞬变电磁衰减曲线及误差图Fig.4 Transient electromagnetic response curve and error of double half-space model

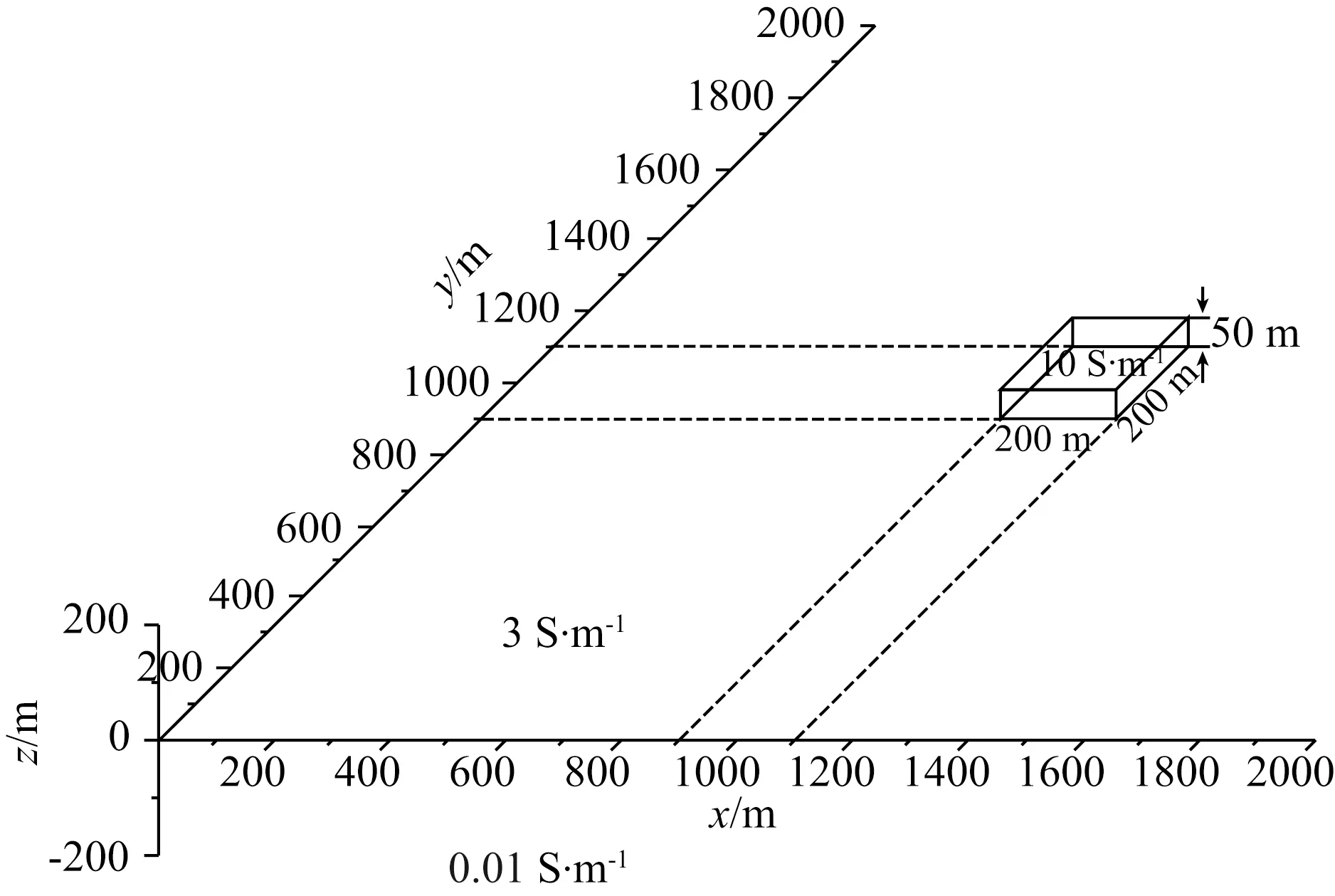
图5 三维模型图200 m×200 m×50 m的硫化物矿体位于洋底面，电导率为10 S·m-1，海水及洋底半空间电导率分别为3 S·m-1和0.01 S·m-1.Fig.5 Three dimentional modelThe cuboid indiactes the VMS deposit which is located on the seafloor with dimensions of 200 m×200 m×50 m. The conductivity of the VMS deposit is 10 S·m-1, while the conductvities of seawater and seafloor are 3 S·m-1 and 0.01 S·m-1 respectively.

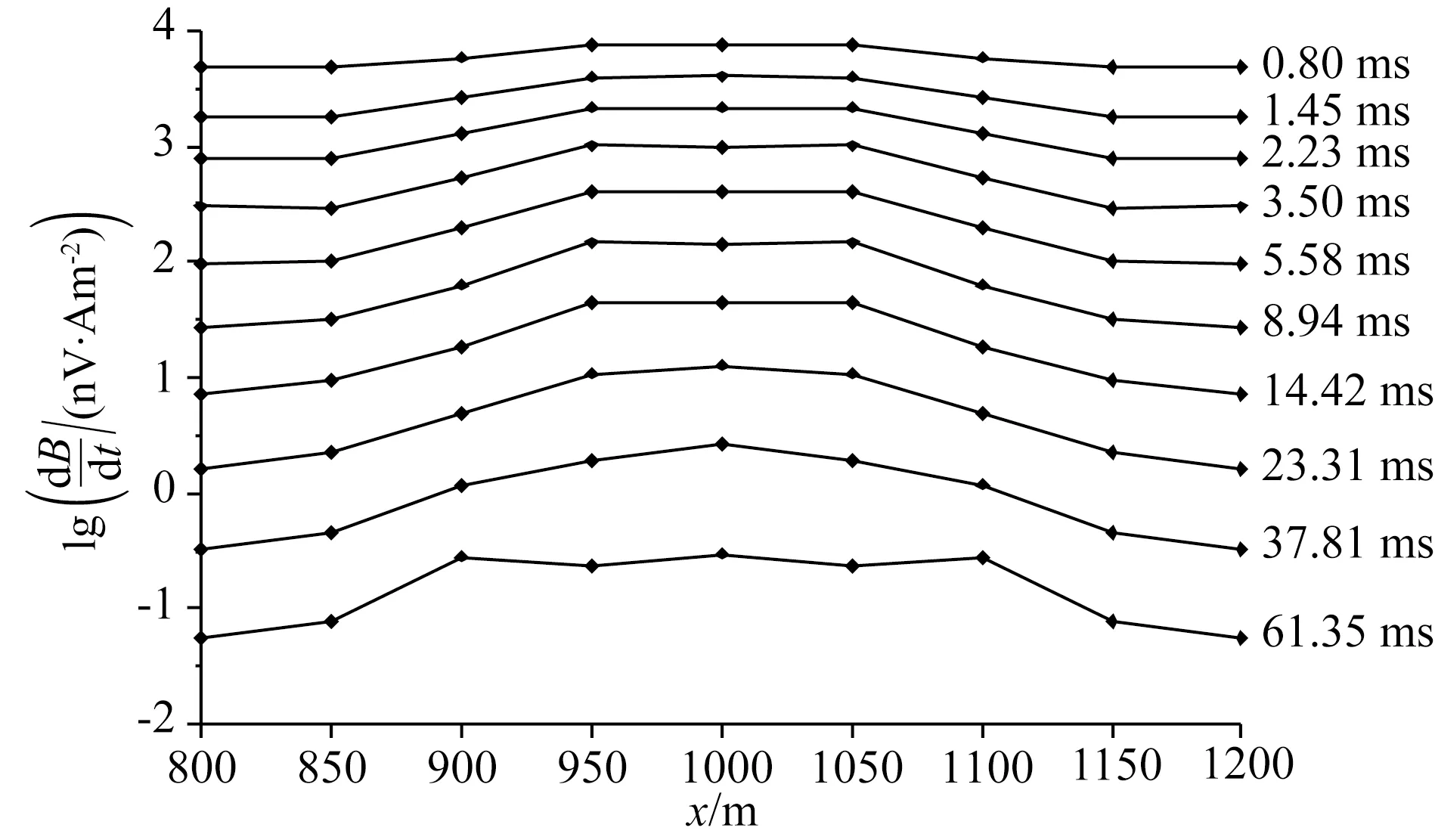
图7 主测线瞬变电磁响应多测道剖面图Fig.7 Transient electromagnetic response multichannnel profile of main line

由图7及图8可见，异常体以外区域，响应值低且平缓，变化不大；在异常体边界处，响应值由异常体外部至内部陡然增大，至一定幅值后趋向平缓，形成形似异常体的高响应值平台，响应异常形态极好地反映了异常体形态，二者近似一致.对比早期、中期、晚期的观测信号，早期响应幅值更高，且更清晰的反映异常体形态，信号幅值随时间衰减，且形态偏向平滑，此时响应异常形态由方形向圆形渐变.此变化主要由于随时间推移，电磁信号主要来自深部地层，出露于洋底的硫化物矿响应影响逐渐减小，响应异常形态趋向模糊.

4 物理实验

为验证数值模拟结果，根据物理模拟相似性准则设计并进行物理实验(Nabighian, 1987).实验仪器采用湖南五维地质科技公司的MTEM-08海洋瞬变电磁仪，发射线圈及接收线圈采用直径为10 cm的圆形线圈，激发电流波形为双极性矩形方波，发射频率6.25 Hz.实验采用120 cm×120 cm×85 cm水槽模拟全空间，水槽下方模拟高阻洋底半空间，水槽底部中心放置20 cm×20 cm×5 cm铜板模拟低阻深海热液硫化物矿.水槽内注入盐水模拟海水，观测线距5 cm，点距5 cm，拖曳高度5 cm，即发射及接收线圈沿铝板上顶面移动.图9是取所有观测点不同时间道数据绘制的电流归一化磁场响应图，由图可见，物理实验采集的数据受到一定干扰，存在误差，但整体规律与数值模拟趋势一致，说明了数值模拟结果的正确性.

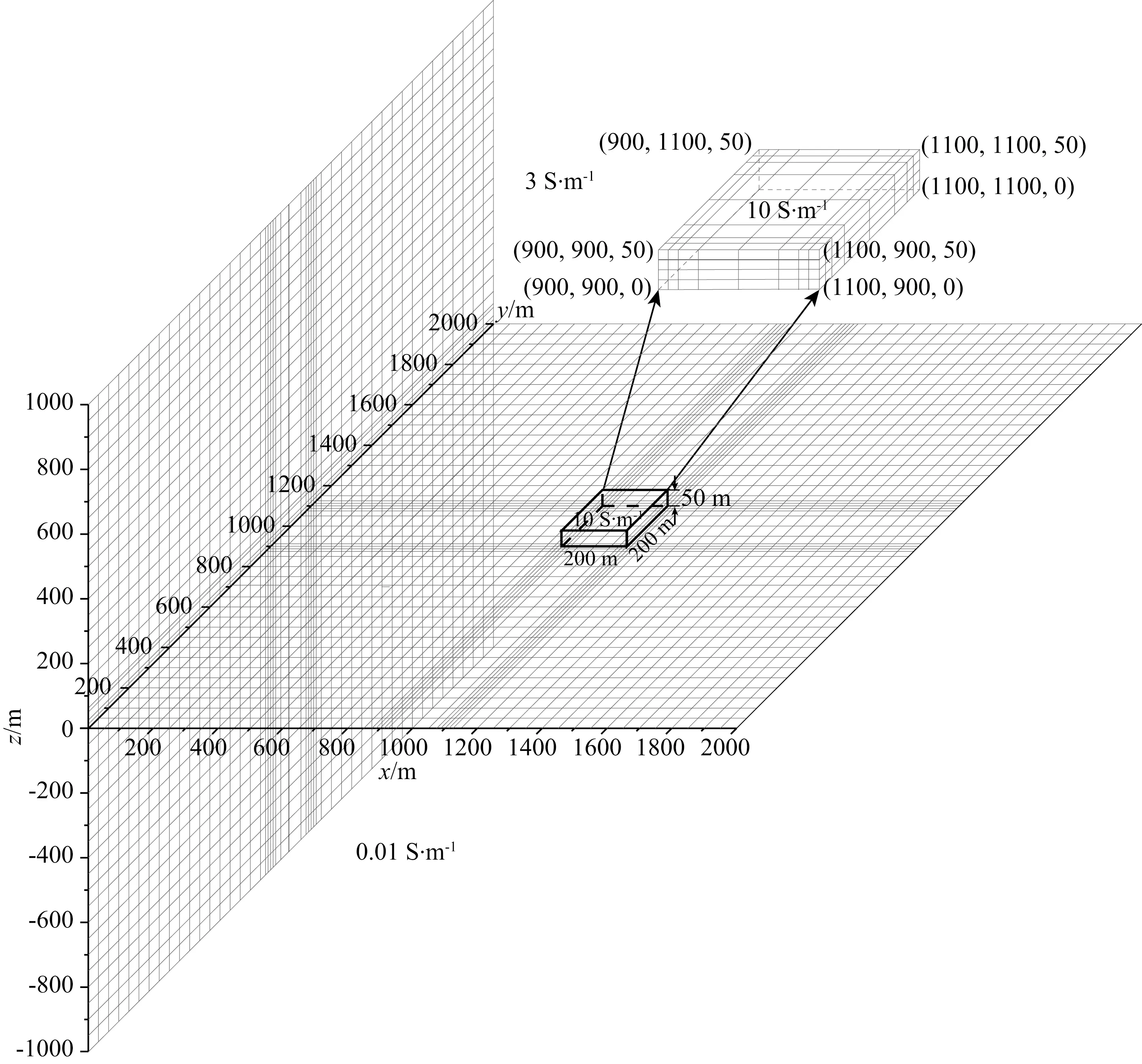
图6 3D模型剖分图Fig.6 Discretization graph of three-dimensional model

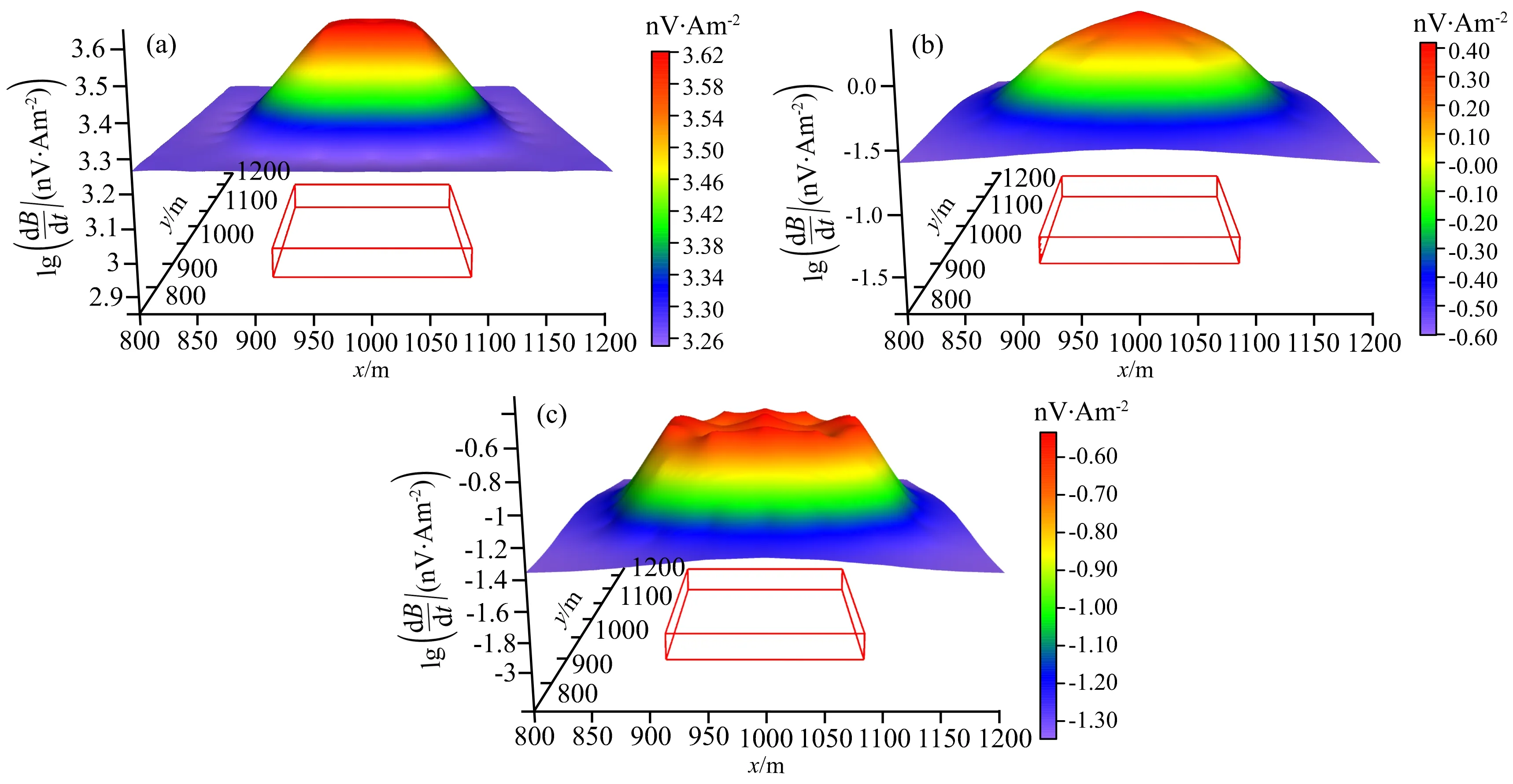
图8 数值模拟3D瞬变电磁响应(a) 1.45 ms; (b) 37.81 ms; (c) 61.35 ms.Fig.8 Numerical simulation of 3D transient electromagnetic response(a) 1.45 ms; (b) 37.81 ms; (c) 61.35 ms.

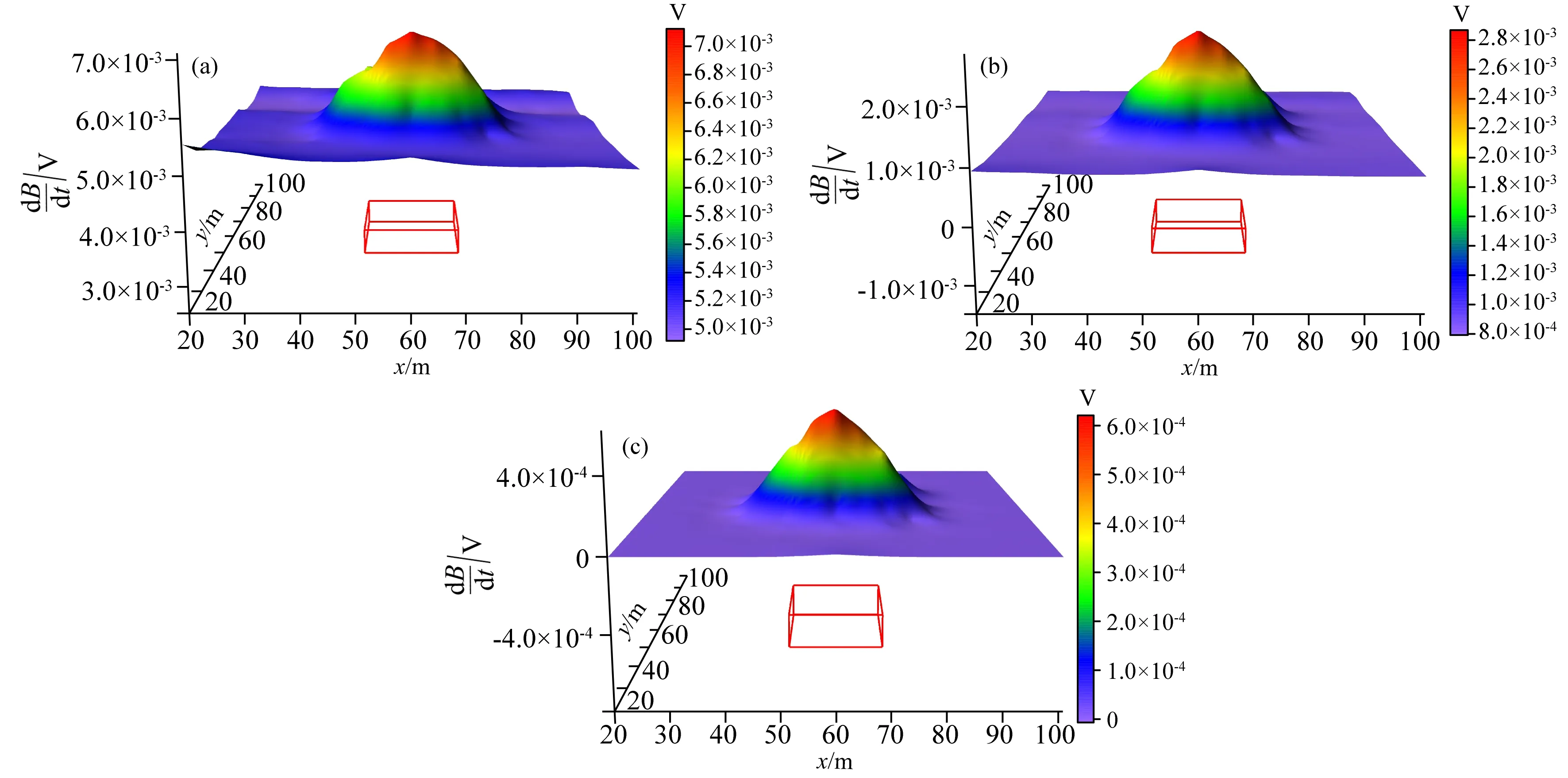
图9 物理模拟3D瞬变电磁响应(a) 0.0016 ms; (b) 0.0096 ms; (c) 0.173 ms.Fig.9 Physical scale modeling of 3D transient electromagnetic response

5 结论

(1) 采用全空间矢量有限元法，对硫化物矿体采用矩形单元模型剖分，应用Galerkin法推导有限元方程，对频率域响应进行Fourier反变换的计算方案，能够有效地计算出深海热液硫化物矿矿体的瞬变电磁响应.

(2) 通过简化的双半空间模型解析解和三维模型物理模拟分别与矢量有限元数值模拟进行比对，证明了矢量有限元算法计算全空间电磁环境是可行的.

(3) 对于海水、矿体以及围岩复杂电磁边界，应用全空间矢量有限元法模拟计算深海热液硫化物矿瞬变电磁响应异常与物理模拟响应趋势一致，而且计算方法简单精确，异常幅值明显，边界清晰.

Börner J H, Bär M, Spitzer K. 2015. Electromagnetic methods for exploration and monitoring of enhanced geothermal systems—A virtual experiment .Geothermics, 55: 78-87, doi: 10.1016/j.geothermics.2015.01.011.

Cai H Z, Xiong B, Han M R, et al. 2014. 3D controlled-source electromagnetic modeling in anisotropic medium using edge-based finite element method.Comput.Geosci., 73: 164-176, doi: 10.1016/j.cageo.2014.09.008.

Cheesman S J, Edwards R N, Chave A D. 1987. On the theory of sea-floor conductivity mapping using transient electromagnetic systems.Geophysics, 52(2): 204-217, doi: 10.1190/1.1442296.Cheesman S J, Edwards R N, Law L K. 1990. A test of a short-baseline sea-floor transient electromagnetic system.Geophys.J.Int., 103(2): 431-437, doi: 10.1111/j.1365-246X.1990.tb01782.x.

Danielsen J E, Anken E, Jørgensen F, et al. 2003. The application of the transient electromagnetic method in hydrogeophysical surveys.J.Appl.Geophys., 53(4): 181-198, doi: 10.1016/j.jappgeo.2003.08.004.

Deng X G. 2007. The deposits and mineral compositions of hydrothermal sulphides in mid-ocean ridge.GeologicalResearchofSouthChinaSea(in Chinese), (1): 54-64.

Evans R L, Everett M E. 1994. Discrimination of hydrothermal mound structures using transient electromagnetic methods.Geophys.Res.Lett., 21(6): 501-504, doi: 10.1029/94GL00418.Herzig P M, Hannington M D. 1995. Polymetallic massive sulfides at the modern seafloor a review.OreGeologyReviews, 10(2): 95-115.

Hu J H, Chang Y J, Lei S L, et al. 2013. 1D forward of TEM of central loop configuration on sea floor and calculation of all-time apparent resistivity.GeophysicalandGeochemicalExploration(in Chinese), 37(6): 1137-1140, doi: 10.11720/j.issn.1000-8919.2013.6.33.

Huang W, Yin C C, Ben F, et al. 2016. 3D forward modeling for frequency AEM by vector finite element.EarthScience(in Chinese), 41(2): 331-342, doi: 10.3799/dqkx.2016.025.

Jang H, Kim H J. 2015. Mapping deep-sea hydrothermal deposits with an in-loop transient electromagnetic method: Insights from 1D forward and inverse modeling.J.Appl.Geophys., 123: 170-176, doi: 10.1016/j.jappgeo.2015.10.003.

Jin J M. 2002. The Finite Element Method in Electromagnetics. New York: Wiley-IEEE Press: 93-113.

Kaufman A A, Keller G V. 1987. Frequency and Transient Soundings (in Chinese). Wang J M Trans. Beijing: Geological Publishing House, 257-273.

Liu C S, Lin J. 2006. Transient electromagnetic response modeling of magnetic source on seafloor and the analysis of seawater effect.ChineseJ.Geophys. (in Chinese), 49(6): 1891-1898.Nabighian M N. 1987. Electromagnetic Methods in Applied Geophysics: Theory. Tulsa, OK: Society of Exploration Geophysicists: 175-177.Sugeng F. 1998. Modeling the 3D TDEM response using the 3D full-domain finite-element method based on the hexahedral edge-element technique.ExplorationGeophysics, 29(3-4): 615-619.Swidinsky A, Hölz S, Jegen M. 2012. On mapping seafloor mineral deposits with central loop transient electromagnetics.Geophysics, 77(3): E171-E184, doi: 10.1190/geo2011-0242.1.Swidinsky A, Hölz S, Jegen M. 2015. Rapid resistivity imaging for marine controlled-source electromagnetic surveys with two transmitter polarizations: An application to the North Alex mud volcano, West Nile Delta. Geophysics, 80(2): E97-E110, doi: 10.1190/geo2014-0015.1.

Xi Z Z, Li R X, Song G, et al. 2016. Electrical structure of sea-floor hydrothermal sulfide deposits.EarthScience(in Chinese), 41(8): 1395-1401, doi: 10.3799/dqkx.2016.110.Yu L, Evans R L, Edwards R N. 1997. Transient electromagnetic responses in seafloor with triaxial anisotropy.Geophys.J.Int., 129(2): 292-304, doi: 10.1111/j.1365-246X.1997.tb01582.x.Zhou S, Xi Z Z, Song G, et al. 2012. Responses of the towed transient electromagnetic sounding on deep seafloor.Journalof

CentralSouthUniversity(SicenceandTechnology) (in Chinese), 43(2): 605-610.Богданов Ю A. 1994. Modern Ocean sulfide deposits category.ChenBYTrans.MarineGeology(in Chinese), (4):18-30.

附中文参考文献

邓希光. 2007. 大洋中脊热液硫化物矿床分布及矿物组成. 南海地质研究, (1): 54-64.

胡俊华, 昌彦君, 雷胜兰等. 2013. 海洋TEM中心回线装置一维正演及全时域视电阻率计算. 物探与化探, 37(6): 1137-1140, doi: 10.11720/j.issn.1000-8919.2013.6.33.

黄威, 殷长春, 贲放等. 2016. 频率域航空电磁三维矢量有限元正演模拟. 地球科学, 41(2): 331-342, doi: 10.3799/dqkx.2016.025.

考夫曼 A A, 凯勒 G V. 1987. 频率域和时间域电磁测深. 王建谋 译. 北京: 地质出版社, 257-273.

刘长胜, 林君. 2006. 海底表面磁源瞬变响应建模及海水影响分析. 地球物理学报, 49(6): 1891-1898.

席振铢, 李瑞雪, 宋刚等. 2016. 深海热液金属硫化物矿电性结构. 地球科学, 41(8): 1395-1401, doi: 10.3799/dqkx.2016.110.

尤·阿·博格达诺夫. 1994. 大洋现代硫化物矿藏分类. 陈邦彦译. 海洋地质, (4): 18-30.

周胜, 席振铢, 宋刚等. 2012. 深海拖曳式瞬变电磁的响应规律. 中南大学学报 (自然科学版), 43(2): 605-610.

(本文编辑 汪海英)

The 3D transient electromagnetic forward modeling of volcanogenic massive sulfide ore deposits

LI Rui-Xue1, WANG He1, XI Zhen-Zhu1*, LONG Xia1,2,HOU Hai-Tao1,2, LIU Yuan-Yuan1, JIANG Huan1

1SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China2Hunan5DGeosciencesCo.,Ltd,Changsha410025,China

The transient electromagnetic forward modeling of volcanogenic massive sulfide (VMS) ore deposits is to calculate the eddy currents electromagnetic response of a three dimensional body in the full space of deep-sea environment. We simulated the three dimensional transient electromagnetic response of the VMS deposits using full-domain vector finite element method. The ore body was discretized with brick rectangular elements. The finite element equation was deduced in frequency domain by employing Galerkin procedure, and the conversion to time domain is using inverse Fourier transform. We confirmed the validity of the full-domain vector finite element algorithm by comparing simulated results with analytical solutions of double half-space model. The results have a good agreement with each other which indicates that the vector finite element method is capable of solving whole space problem. In order to demonstrate the ability of the numerical method in calculating the response of VMS deposits containing complex boundary conditions, we compared vector finite element solution of a three dimensional electrical model with physical experiment results according to electromagnetic physical scale modeling rules. The comparison suggests that for the complex electromagnetic boundary of seawater, ore body and country rocks, the transient electromagnetic response of VMS deposits calculated by full-domain vector finite element method has same features with the physical scale modeling result. The vector finite element method is simple and its results are precise with obvious and clear anomaly response.

Volcanogenic massive sulfide ore deposit; Vector finite element method; Marine transient electromagnetic method; Whole-space 3D forward modeling

10.6038/cjg20161213.

国际海域资源调查与研发“十二五”(DY125-11-R-03),深圳市未来产业发展专项资金项目(HYZDFC20140801010002),海南省科技兴海专项(2015XH07)共同资助.

李瑞雪，女，1987年生，在读博士生，主要从事海洋瞬变电磁正演计算研究.E-mail:liruixue0911@163.com

*通讯作者 席振铢，男，教授，博士，主要从事瞬变电磁原理、技术及应用研究.E-mail:xizhenzhu@163.com

10.6038/cjg20161213

P631

2016-01-29，2016-09-28收修定稿

李瑞雪， 王鹤， 席振铢等. 2016. 深海热液硫化物矿体3D瞬变电磁正演. 地球物理学报，59(12):4505-4512,

Li R X, Wang H, Xi Z Z,et al. 2016. The 3D transient electromagnetic forward modeling of volcanogenic massive sulfide ore deposits.ChineseJ.Geophys. (in Chinese),59(12):4505-4512,doi:10.6038/cjg20161213.