基于藤Copula-MCMC-SV-T模型的马航空难对六国（地）股指的风险传染研究

韩 超，严太华

（重庆大学经济与工商管理学院，重庆400030）

基于藤Copula-MCMC-SV-T模型的马航空难对六国（地）股指的风险传染研究

韩 超，严太华

（重庆大学经济与工商管理学院，重庆400030）

2014年马航MH370和MH17两次空难，引发世界人民的焦虑。焦虑从马航空难直指世界矛盾冲突，矛盾冲突导致恐慌。恐慌引起股市多空异常行为，引发股市风险，风险从吉隆坡传出，向世界蔓延。论文以SV-T模型刻画六维边缘股指波动进程，以MCMC算法的Gibbs抽样方法贝叶斯推断出边缘模型参数，以C藤Copula结构描述世界六国（地）股指风险传染路径图，以四种常见类型的Copula函数代表四种不同的风险传染类型，以相应的Copula函数Tau值表示风险传染参数，最终描绘出空难引起的危机从吉隆坡向世界蔓延的脉络和风险强度。论文尝试为投资者面对突发事件时进行多、空投资决策，以及管理当局把握危机传染路径、降低风险连锁反应，斩断风险传染链条提供一种新的思路和方法。

马航空难；危机传染；C藤Copula；MCMC；SV-T

一、空难背景

2014年马航两次空难，MH370和MH17，共造成537人失踪或者遇难，直接或间接影响几十个国家，造成重大损失。透过现象看本质，两次空难都体现了国际主义精神是人类合作的新方向，但地缘政治思维的枷锁却依然束缚于每个国家。MH370失联后，包括中国、俄罗斯、美国和德国在内的众多国际力量加入了这场政治博弈，失联搜救区域变成了一个全球舞台，演化成多种力量的国际博弈场；MH17被导弹击落，本身是地缘政治的牺牲品，或许又将深刻影响全球政治格局。

两次空难背后体现的是政治问题，政治是经济的表象，作为经济晴雨表的金融市场亦有所反应。空难发生后，由宗教矛盾、民族矛盾、贫富矛盾、不同利益集团矛盾等产生的不确定因素导致全球市场恐慌指数大幅上升，投资者避险情绪明显增长。MH370失联后的首个交易日，亚洲股市，尤其是东南亚股市中的马来西亚股指、新加坡海峡时报股指以

及我国香港恒生指数均不同程度下跌；亚洲以外的市场也表现出悲观预期，德国DAX指数、道琼斯工业平均指数、纳斯达克100指数均有不同程度下跌。MH17被导弹击落事件触发全球避险行为：黃金、国债以及日元等避险资产受到投资者追捧，芝加哥期权交易所波动指数表现出年内最大单日升幅。

二、文献综述

Copula方法能够准确描述金融变量间的非线性相关，可以应用于金融波动溢出和风险传染研究领域。大量的研究文献证实了这一点，其中：Juan（2007）、叶五一（2009）、王永巧（2011）、黄在鑫（2012）、顾冬雷（2013）［1-5］利用Copula研究不同市场间的风险传染问题。目前Coupula理论的前沿问题之一是高维化应用，其高维化主要有两种方法：一是传统的多元Copula方法，代表性研究主要有：Joe（1997）、Nelson（1999）、刘志东（2006）［6-8］等；二是藤结构的Pair-Copula运用，代表性研究主要有：Bedford&Cooke（2001）、Kurowicka&Cooke（2006）、Aas et al.（2009）、高江（2013）［9-12］等。

在构建Copula函数过程中，边缘分布的高质量刻画至关重要。Kim Shephard（1998）、Harvey A（1994）、Poon Granger（2003）以及余素红（2002）［13-16］等已经证明，SV模型在刻画金融波动方面优于ARCH和GARCH类模型，能更好地描述金融数据特性，具有较强的波动预测能力。但是，由于SV模型含有隐随机变量，估计过程极其复杂，受限于计量方法和计算问题，该方法并没有得以广泛运用，直到20世纪90年代计量建模和计算机技术的突破，SV模型才更为广泛的为广大学者所应用。SV模型的估算最常用的是MCMC算法，在众多研究中，Jacquier E（1994）［17］率先用MCMC方法贝叶斯推断SV模型，得到优于伪似然估计和矩方法的结论，之后，Jacquier E（2004）、Yu&Meyer（2006）［18-19］进一步用该方法估计扩展SV模型参数，得到较为理想的结论。MCMC方法的本质是模拟一个特定的收敛于某个平稳转移分布的马尔可夫过程，而该马尔可夫过程的建立方法主要有Metropolis算法、Metropolis-Hastings算法以及Gibbs抽样方法，其中以Gibbs抽样最为流行。Gibbs抽样方法由Geman夫妇（1984）［20］首先提出，其后，Gelfand and Smith（1990）［21］证明了Gibbs抽样可以应用于多种形式的后验分布估算，从而将Gibbs抽样为基础的MCMC算法应用于贝叶斯统计推断的研究中。

本文以C藤Copula模型研究2014年发生的马航MH370和MH17两次空难对于世界六国（地）股指的危机传染问题，在拟合藤结构时采用SV-T模型刻画边缘分布波动，用MCMC算法的吉布斯抽样进行贝叶斯推断，求得SV-T模型的参数；论文将数学函数和相应参数的含义引申，以四种Copula函数代表不同风险传递类型，以τ（Tau）值描述风险传递强度，进而绘制出以风暴中的马来西亚吉隆坡股指为核心传染源的世界六国（地）危机传染效应路径图。本研究尝试为当今不确定性政治经济环境下的危机传染和危机控制提供一种新的思路和方法。

三、理论与模型

（一）Copula函数、非线性相关和风险传染

Copula函数由Sklar（1959）［22］首次提出，其形式和性质可以表示为：设随机变量X1,X2,…,Xn，对应的边缘分布函数分别为F1,F2,…,Fn，联合分布函数为F，则存在着一个Copula函数，使得：，也就是说Copula函数可以将n维联合分布函数分解为n个边际分布与一个Copula，从而更好地描述n维变量的相依性。这样就在高维建模时将边际分布建模与Copula函数拟合分离进行，更具灵活性。大量研究证明，Copula函数能够把具有非线性相依关系的多维变量“连接”起来，可以克服传统线性相关无法准确描述金融时间序列之间非线性关系的问题，基于这一优点，21世纪初Copula方法逐渐应用到金融变量间非线性相关的研究。

本文在进行研究时，选择四种最常见的Copula函数，分别是：Gauss-Copula、t-Copula、Clayton-Copula和Gumbel-Copula。其中，Gauss-Copula函数，描述的是整体相依关系，其与t-Copula函数都具有分布的对称性，但是t-Copula函数具有更厚的尾部，能够描述金融变量间的尾部相依，两者都属于椭圆Copula族，而Clayton-Copula和Gumbel-Copula则属于阿基米德Copula族，具有分布的非对称性，其中Clayton-Copula侧重于描述下尾正相关，而Gumbel-Copula侧重于描述上尾正相关。根据这四种Copula函数的特性，本文赋予参数指标更多的现实意义：Gauss-Copula在四种函数中最能代表均匀的整体对称相关，我们以其参数测度金融变量间的整体性传染；t-Copula代表对称的厚尾分布相关，测度双尾的风险传染；Clayton-Copula代表非对称的下尾正相关，着重测度下尾的风险传染；Gumbel-Copula代表非对称的上尾正相关，着重测度上尾的风险传染。

传统的研究关注的是下尾风险，本文拟将此关注点引申，同时关注上尾和下尾风险，原因在于股指期货市场的发达使得做空交易盛行，金融市场不再仅仅是多头市场。在多空博弈的股票期货和现货市场中，多头关注下尾风险，以Clayton-Copula描述；空头关注上尾风险，以Gumbel-Copula描述，t-Copula同

时描述对称的双尾风险传染，而Gauss-Copula描述整体性传染，这样就把理论与本文研究的风险传染实际结合了起来。关于四种Copula函数理论更详尽的基础描述，本文不再赘言，可参见韦艳华等（2008）［23］的研究。

（二）单个金融序列的残差过滤模型和MCMC算法

SV模型由Taylor（1986）［24］率先提出，SV较之GARCH类模型更能描绘金融时间序列的尖峰厚尾性，更具稳定性和预测性，其假定序列的时变波动性服从某种随机过程，不依靠过去的信息。本文采用SV-t模型拟合Copula函数的边缘分布，能够更好地刻画金融序列的厚尾形态，形式如式（1）所示：

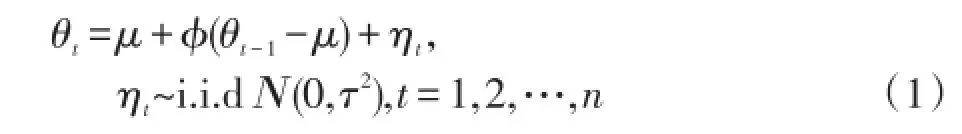
其中，yt表示股指收益率序列，θt表示对数波动率；εt表示独立同分布的白噪声干扰，假设服从自由度ω的t分布；ηt服从均值为0、方差为τ2的正态分布，序列ηt与εt均不可观测，且互不相关；ϕ表示θt前期影响的持续性，在|ϕ|＜1的情形，SV-t模型所描述的波动过程是协方差平稳过程。本文采用基于Gibbs抽样方法的MCMC算法来实现SV模型的估计。

（三）C藤Copula结构与拟合算法

本文研究的是六维数据，采用六维C藤Copula结构，如图1所示，相应的算术表达为式（2）：

图1 六维C藤Copula结构

在高维C藤，模型拟合的过程中，h函数至关重要，根据Joe（1997）［6］，h函数形式如式（3）所示：

其中，v表示条件变量，Θ表示x和v联合分布的Copula参数集。

结合六维C藤Copula结构图1进行C藤模型拟合时，一棵树（T）的一个层次的Copula参数决定了对应的h序列，h序列又决定了下一棵树（T）的对应层次的条件Pair-Copula函数的参数，这样不停地依据上一层的参数估计下一层的Copula模型，最终能够估计出整个C藤Copula结构所有树的参数。

（四）基于C藤Copula的危机传染路径图原理

在理解与理顺C藤Copula的危机传染路径图中的关系时，每棵树的边的结点间的斯皮尔曼秩相关系数ρ或者Kendall秩相关系数τ与根据Copula函数类型以及对应参数求出的除第一条边以外的各边的结点至关重要。根据韦艳华（2008）［23］关于ρ和τ的概念以及公式（4）、（5）：

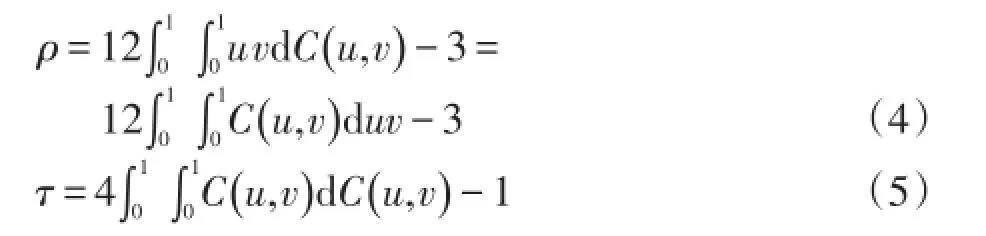
再根据双重积分的定义，我们可以把（4）式中右边的积分部分想象为一个柱体，柱体的高即是C(u,v)，当然累积分布函数C(u,v)≥0，假定C(u,v)非常数，根据Nelson（2006）［25］可知，0＜∂C(u,v)/∂u,∂C(u,v)/∂v≤1，说明C(u,v)同时又分别是u,v的递增函数，这样柱体的体积在与高成正比的同时，也与底面积成正比，这就排除了在（4）式中ρ与C(u,v)成正比的同时会与uv成反比的可能性，就可以推断出ρ是C(u,v)的单调增函数。同理，在（6）中可以把积分部分想象为底和高均为C(u,v)的柱体，而累积分布函数0＜C(u,v)≤1，所以τ也是C(u,v)的单调增函数，进而说明无论Copula函数的类型，τ和ρ都存在着单调增函数关系。再根据Nelson（2006）［25］，对于∀u,v∈[0,1]偏微分∂C(u,v)/∂u,∂C(u,v)/∂v都存

在，并且0≤∂C(u,v)/∂u,∂C(u,v)/∂v≤1，而这种偏微分也可以理解为相应形式的（条件）h函数，这就说明结点的值与相应的Copula函数值是存在非减关系的，进而说明C(u,v)非常数时，根据ρ求得的各边的结点和ρ存在着单调增函数关系，同样也说明τ与结点间存在着这种单调增关系。这样，我们就可以通过分析ρ和τ中的任一值的变化观察风险传染现象，本文选择以τ值进行研究。

根据Aas（2009）［11］，当一组变量中的某个变量在数据集中起到主导作用时，就可以采用C藤结构描述变量间的关系，而该变量就应该处于C藤的根部位置。本文出于研究需要，为了突出马航空难的风险传染效应，人为地将马来西亚股指置于C藤的根部，以研究马来西亚股指这一变量的波动如何影响到其余变量，这样就能够以吉隆坡为传染起点，顺着C藤的结点、边和树观察传染进程和强度，这样的一种运用与Aas（2009）［11］的观点不但不矛盾，还是对其C藤概念应用的引申，当然，所有的研究都建立在客观的数据、客观的方法以及得出的客观的结论基础之上的。在研究传染进程时，我们分两种情况进行分析：当风险传染类型转换后为同一种除Gauss-Copula函数之外的风险代表类型时，如图1中，当第一棵树的连接1和2两个结点的边上的相应的Copula函数类型的参数增大时，我们就可以知道第二棵树的第一条边的左边的结点会增大，同样，第一棵树的连接1和3两个结点的边上的相应的Copula函数类型的参数增大时，第二棵树的第一条边的右边的结点也会增大，这样第二棵树的第一条边的两边的结点都增大了，进而第二棵树的第一条边上的Copula函数类型的参数就会同时增大，我们就认为发生了风险传染；同时，风险的传染还以风险类型的变化来体现，当风险传染类型转换为除了Gauss-Copula之外的另一种Copula函数类型时，无论参数增大与否，我们都认定发生了风险传染。而这种风险传染不仅仅发生于第一棵树上的结点1和结点2，结点1和结点3之间，还因为这两条边之间的风险传染传导至第二棵树，使得第二棵树的第一条边的左右两结点之间产生了风险传染问题。根据这种思考方式，我们就可以梳理出C藤结构中每棵树的各条边和各结点之间的风险传染的实际进程、传染类型和传染强度，并且据以画出带有因果方向性的危机传染路径图，见后文图4和图5。

四、实证研究

（一）两次空难基本情况

2014年，马航祸不单行，北京时间3月8日MH370失联，至今杳无音信，7月17日MH17被击落，两次空难共计超过500人遇险。空难的突然发生引来全世界焦虑的目光，焦虑从空难延伸到复杂的世界政治与经济，形势的不确定性再次成为关注焦点。出于研究需要，本文把MH370和MH17两次空难的相关情况整理成表1。

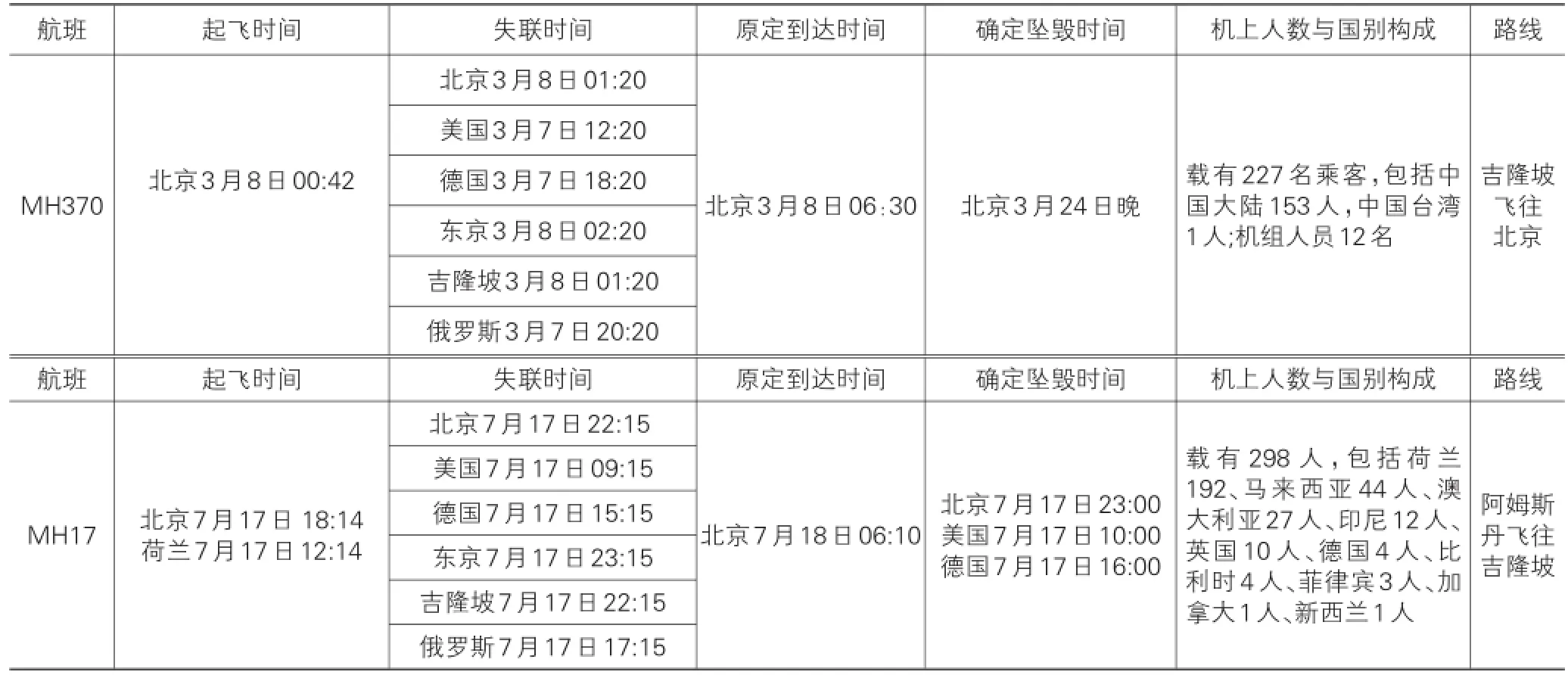
表1 两次空难背景资料

（二）数据处理与统计描述

本文从万德数据库抽取吉隆坡综合指数（KLSE）、美国纳斯达克指数（IXIC）、香港恒生指数（HSI）、俄罗斯指数（RTS）、德国法兰克福指数（GDAXI）以及新加坡海峡指数（STI）六国（地）股指进行研究，时间跨度从2013年8月21日到2014年11月26日。需要说明的是，恒生指数在中国区域股市中影响力很大，是中国区域市场开放度最高、能较全面代表中国区域经济的股指，而沪深股市的市场效率相对较低和开放度不够高，由此本文在研究世

界股指的相依关系时，选取恒生指数代表大中华区经济在马航空难中受到的影响。另外，新加坡是马来西亚的近邻又是离岸金融中心，风险容易从马来西亚传导到新加坡；香港也是金融开放度较高的区域，作为亚洲四小龙之中的香港对于同处于东亚地区的马来西亚空难必然有着敏感的反应；俄罗斯作为东欧地区与东亚的近邻，其经济与股市都与东亚地区有着千丝万缕的联系，俄罗斯本身的政治敏感性又容易受到马航空难的波及，特别是MH17空难直接发生于俄罗斯与乌克兰的矛盾漩涡之中；东欧地区的政治神经归根结底是美国为首的西方阵营与俄罗斯为首的东方阵营对峙的延续，故而代表世界经济发展的美国不能置身局外，本文将美国股市也纳入进来；而德国自从柏林墙倒塌以来仍然没能走出东西阵营对峙的阴影，所以本文的研究以德国股市来观察政治经济敏感性风险如何在东西阵营间进行传导。

在数据处理时，结合基本情况表和世界时区分布特征，把IXIC提前1日的指数与其余股市当日指数相对应，比如MH370于北京时间3月8日01：20失联，对应于美国时间3月7日12：20，正值纳斯达克股市3月7日开盘期间，距离收市还有3小时40分钟，空难有充足时间对IXIC产生影响，同样MH17空难也存在同样的数据处理要求；而其余的股市，如GDAXI和RTS，虽然和北京时间不同，但是时区差别不足以使两次空难的影响迁延到前1个交易日。数据处理时，我们取日间对数收益率rt=ln(Pt/Pt-1)×100%为研究对象，如果有缺值则交易日指数往后递延。根据这种数据处理方法和两次空难的时间节点，我们将数据分成2013年8月21日到2014年3月7日（IXIC从2013年8月20日到2014年3月6日）共100×6组数据，2014年3月12日到2014年7月17日（IXIC相应提前1日）共68×6组数据，2014年7月18日到2014年11月27日（IXIC相应提前1日）共75×6组数据，分别为这三段数据命名为“空难前”、“空难中”、“空难后”，简称“前”、“中”、“后”。本文研究结论借助于MATLAB、R和Winbugs语言编程实现。

（三）数据边缘分布拟合

对于空难前、空难中和空难后的3X6组时间序列，本文采用SV-T模型分别进行过滤，模型拟合通过吉布斯抽样的贝叶斯推断来实现，根据美国学者Kim和Shephard（1998）［26］以及新西兰学者Renate& Jun（2000）［27］的观点，可以将模型（1）式参数的先验分布设定为式（6）所示：

推断过程中，每次MCMC算法都以前1 000次为燃数期，继而分别进行50 000次双链模式的马氏链构造，双链模式的马氏链有助于我们观察数据拟合是否收敛，初始值由程序随机产生。出于精简篇幅考虑，仅以空难中和空难后为例，相应的部分主要参数推断结果见表2-表3所列。

表2 空难中SV-T贝叶斯后验参数推断表

表3 空难后SV-T贝叶斯后验参数推断表

续表3

结合各参数的均值和标准误以及蒙特卡罗误差，我们认为拟合效果很好，参数估计很显著，为了进一步观察拟合质量，我们以空难中和空难后厚尾T分布参数ω（omega）的双链收敛效果和历史轨迹图2-图3为例，可以看出六国（地）股指参数的阶段数据推断效果比较理想，其余参数也类似，文中不再陈列。

图2 空难中贝叶斯参数收敛图

图3 空难后贝叶斯参数收敛图

如图2-图3，参数的双链后验轨迹图说明了马尔可夫链的收敛性和稳定性，后验自相关图说明了参数估计在1阶之后自相关迅速弱化，佐证了推断的收敛性。

边缘参数确定之后，运用相应的模型对时间序列进行过滤，可以得到相应的标准残差，对标准残差进行概率积分变换（PIT），使之转换为服从U（0，1）分布的PIT序列，运用K-S检验效果如何，表4-表6分别展示的是空难前、中、后三个阶段SV-T建模后，PIT序列比较理想的K-S检验效果。

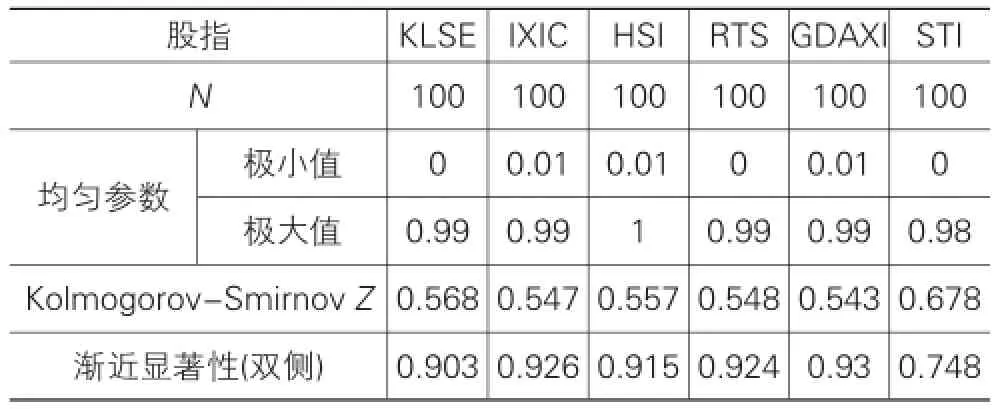
表4 空难前单样本Kolmogorov-Smirnov检验

表5 空难中单样本Kolmogorov-Smirnov检验

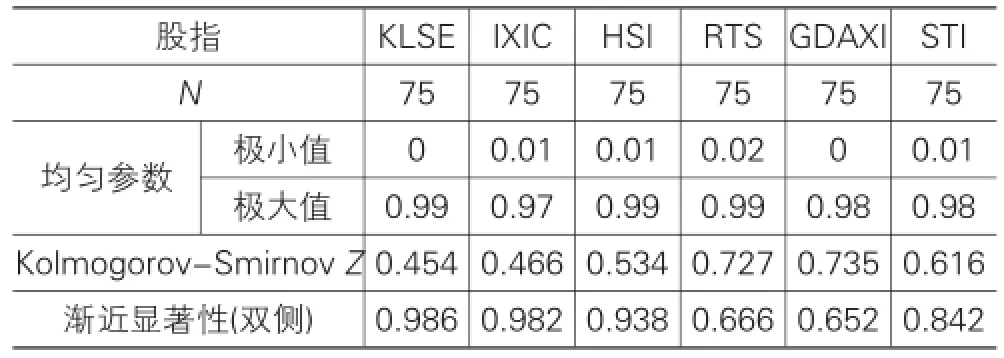
表6 空难后单样本Kolmogorov-Smirnov检验

（四）C藤Copula结构与风险传染

接下来对空难前、中、后的PIT序列组分别进行C藤Copula结构建模。我们考察的是马航空难的影响，考虑的是吉隆坡指数风险对于世界其他五国股指的传染效应，所以我们以吉隆坡指数为引导变量，由其出发构建空难前、空难中和空难后五棵树的C藤结构图，进而比较包括风险类型和风险强度在内的风险传染效应。这里需要阐明：同样的多维数组可以有很多不同的C藤结构具体形式，只要关键变量确定了，具体形式如何变化，只会影响危机传染图的具体表现形式，（条件）变量之间相关性结构的类型与强度不会发生实质性的改变。

根据PIT序列进行藤结构绘图，可以发现空难前、空难中和空难后的风险类型和风险强度产生了明显的改变，为了便于比较，我们把空难前、中、后三个阶段的藤结构绘图比较结果以表7形式体现：其中，数字1-6分别代表了我们研究的六国（地）股指：KLSE、IXIC、HSI、RTS、GDAXI、STI。

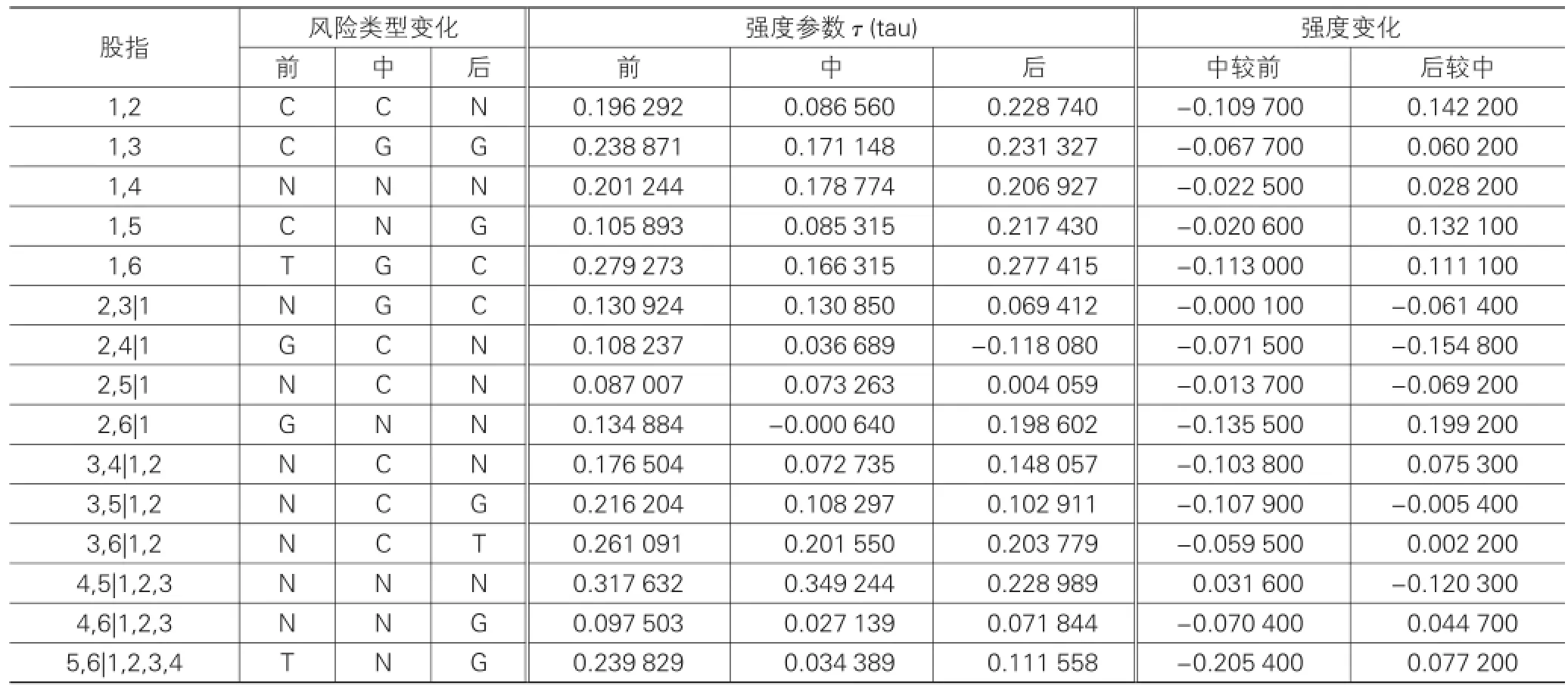
表7 两次空难藤结构参数变化

根据表7，综合考虑强度参数和风险类型的变化，依据3.4节的危机传染路径图原理，我们可以绘制风险传染图4和图5。其中，N、T、C、G分别表示Gauss Copula、T Copula、Clayton Copula、Gumbel Copula四种类型的Copula。这里需要说明风险传染分析的具体方法：我们把风险定义为尾部的风险，做空看的是上尾风险，多发生在股指期货市场，做多看的是下尾风险，发生在股指现货市场，主要就是股市；当上尾风险积聚，价格区位在上方躁动，容易引起看空者砸盘，使期指走低，而期指对于现指具有引导作用，导致现指走低，当下尾风险积聚，原有做多者会抛盘，新入做多者则会抄底买进；认定不同的Copula函数类型代表不同的风险状态，Gauss Copula代表整体相依，不强调尾部，即使Tau值增强，仍不认为存在尾部风险传染；T Copula函数代表对称的尾部风险的积聚，Tau值的增强说明看多和看空风险相依的势均力敌；Clayton Copula函数描述下尾风险相依，说明风险更多的是通过做多者关注的下尾风险传递；Gumbel Copula函数描述上尾风险相依，表明风险是通过看空者关注的上尾风险蔓延的。

针对表7和风险传染阐释，列举两例进行实际的风险传染分析，其余分析可依此类推：

吉隆坡和纳斯达克中的连接函数类型较前仍为Clayton Copula，说明风险类型未变，参数Tau值反而降低，说明二者之间不存在风险传染迹象，而后较中连接函数类型变为Gauss Copula，且参数Tau值有显著增长，说明二者的整体相依性增强了，但是我们仍然不认为二者有风险传染发生，因为我们所认定的

风险发生在上尾或者下尾。因此，我们认为，两次空难都没有在吉隆坡和纳斯达克股票市场间产生危机传染效应。吉隆坡和香港恒生中的连接函数较前变为Gumbel Copula，参数Tau值下降，说明风险向上尾积聚，尽管相依性更弱，我们仍然认为发生了上尾风险传染，而后较中虽然相依性更强，风险类型却转变为Gauss Copula，我们只能认为二者整体相关增强，却没有侦测到风险传染。

相应的风险传染图形如图4和图5，其中风险传染与方向以箭头线段表示，大写字母表示相应Copula函数的首字母，同时指代风险传染类型和状态，大写字母前的（条件）数字指代相应变量的（条件）关系，虚线表示增强的整体相依，无风险传染。风险传染方向本着危机传染路径图原理中的因果关系，第一核心传染源定位为吉隆坡综指，风险从吉隆坡传出，按照树形图的边和结点依次传染。需要指出的是与吉隆坡直接关联的风险传染都是普通的Copula函数关联，与吉隆坡间接关联的两两股指之间的Copula函数则为条件Copula，如图4中的香港恒生和美国纳斯达克股指之间则是以吉隆坡股指为条件的Gumbel Copula函数关系，图中吉隆坡把风险传染给了香港，故而我们认为以吉隆坡股指为条件时，香港恒生把风险传递给了美国纳斯达克股指，标记为23|1G。

图4 空难中C藤结构危机传染图

图5 空难后C藤结构危机传染图

五、结论与学术意义

根据前面的研究结合传染图4和传染图5，本文梳理出风险传染的脉络并得出如下结论：

MH370空难发生后，对应于空难中C藤结构危机传染图可以发现：吉隆坡以上尾风险的形式同时传递给新加坡海峡和香港恒生指数，新加坡海峡和香港恒生指数在给定吉隆坡和纳斯达克股指的条件下，存在着单向的下尾风险传染，而香港恒生进一步把上尾风险传递给纳斯达克，纳斯达克又同时以下尾风险的形式同时传递给法兰克福和俄罗斯。与此同时，香港恒生又同时把下尾风险传递给法兰克福和俄罗斯指数。

从空难中危机传染图可以发现：MH370空难发生后，法兰克福和俄罗斯指数的整体相依增强了，但是二者不存在直接的传染关系；MH17空难发生后，对应于空难后危机传染图，我们发现吉隆坡综指把上尾风险同时传递给了香港恒生和法兰克福，把下尾风险传递给了新加坡海峡指数，而香港恒生和新加坡海峡指数之间存在着双向的双尾对称风险传递，新加坡和法兰克福存在着双向的上尾风险传递，进一步香港恒生把下尾风险传递给了纳斯达克指数，把上尾风险传染给了法兰克福。与此同时，我们也可以发现MH17空难发生后，吉隆坡和俄罗斯、香港恒生和俄罗斯、纳斯达克和吉隆坡，以及新加坡海峡与纳斯达克之间的整体相依性显著增强了。

结合两次空难传染图，还可以发现：在两次马航空难事件中香港恒生和新加坡海峡指数都起到了直接的风险传染中介作用。香港恒生两次把风险传染给纳斯达克股指，并且在MH370空难中把风险传递给了新加坡；在MH17空难中香港恒生和新加坡海峡指数之间则存在着双向的条件Copula传染关系。新加坡海峡指数以相应的条件相依性把风险传递给了德国法兰克福和俄罗斯股指，而香港恒生则把风险传递给了法兰克福。对两次空难的风险传染进行比较，发现MH17空难的危机传染路径更为复杂，这是因为MH370失联更多体现的是不确定性，而MH17空难明确是战争带来的恐怖，加之对第一次空难危机的风险叠加效应，风险传染方式更加扑朔迷离。

本文尝试以一种新的方法对马航两次空难的风险传染进行研究，期望可以为多、空投资决策和管理当局把握危机传染路径，降低风险连锁反应提供一种新的思路和方法。本文的研究还突破了传统研究只看下尾风险的局限性，指出灾难事件基于股市本身复杂的结构，也可能存在上尾风险，并以四种不同的Copula类型来描述风险传染的不同状态，提供了刻画风险传染的一种新的思路。

下一步研究的方向：①突破藤Copula的结构限制，借助于条件Copula形式，以分层的模式把传染面进一步拓宽；②Copula无方向性，其参数也是标量，还可以借助于格兰杰因果检验赋予其方向，但是需要对格兰杰因果检验进行改进，使其能够检验出非线性关系的时间序列间的因果关系。

［1］Juan C R.Measuring financial contagion：A Copula approach［J］.Journal of Empirical Finance，2007，14（3）：401-423.

［2］叶五一，缪柏其.基于Copula变点检测的美国次级债金融危机传染分析［J］.中国管理科学，2009，17（3）：1-7.

［3］王永巧，刘诗文.基于时变Copula的金融开放与风险传染［J］.系统工程理论与实践，2011（4）：778-784.

［4］黄在鑫，覃正.中美主要金融市场相关结构及风险传染路径研究——基于Copula理论及方法［J］.国际金融研究，2012（5）：74-82.

［5］顾冬雷，叶五一，缪柏其.基于藤Copula方法的区域性金融危机传染分析［J］.中国科学技术大学学报，2013，43（9）：737-744.

［6］Joe H.Multivariate Models and Dependence Concepts［M］. London：A CRC Press Company，1997：83-138.

［7］Nelsen R B.An Introduction to Copulas［M］.New York：Springer，1999：84-88.

［8］刘志东.基于Copula-GARCH-EVT的资产组合选择模型及其混合遗传算法［J］.系统工程理论方法应用，2006，15（2）：149-157.

［9］Bedford T，Cooke R M.Probability density decomposition for conditionally dependent random variables modeled by vines［J］.Annals of Mathematics and Artificial Intelligence，2001，32（1）：245-268.

［10］Kurowicka D，Cooke R.Uncertainty Analysis with High Dimensional Dependence Modelling［M］.Chichester：John Wiley&Sons，2006：81-109.

［11］Aas K，Czado C，Frigessi A，et al.Pair-copula constructions of multiple dependence［J］.Insurance：Mathematics &Economics，2009，44（2）：182-198.

［12］高江.藤Copula模型与多资产投资组合VaR预测［J］.数理统计与管理，2013，32（2）：247-258.

［13］Kim S，Shephard N，Chib S.Stochastic Volatility：Likelihood Inference and Comparison with ARCH Models［J］. Review of Economic Studies 1998，65（3）：361-393.

［14］Harvey A C，Ruiz E，Shephard N.Multivariate stochastic variance models［J］.Review of Economic Studies，1994，61（2）：247-267.

［15］Poon S H，Granger C W J.Forecasting volatility in financial markets：a review［J］.Journal of Economic Literature，2003，41（2）：478-539.

［16］余素红，张世英.SV与GARCH模型对金融时间序列刻画能力的比较研究［J］.系统工程，2002（5）：28-33.

［17］Jacquier E，Poison N，Rossi P.Bayesian analysis of stochastic volatility models［J］.Journal of Business and Economic Statistics，1994，12（4）：371-417.

［18］Jacquier E，Poison，N，Rossi P.Bayesian analysis of stochastic volatility models with fat-tails and correlated errors［J］.Journal of Econometrics，2004，122（1）：185-212.

［19］Yu J，Meyer R.Multivariate stochastic volatility models：Bayesian estimation and model comparison［J］.Econometric Reviews，2006，25（2/3）：361-384.

［20］Geman S，Geman D.Stochastic relaxation，Gibbs distributions and the Bayesian restoration of images［J］.Transactions on Pattern Analysis and Machine Intelligence，1984，8（6）：721-741.

［21］Gelfand A E，Smith A F M.Sampling-based approaches to calculating marginal densities［J］.Journal of American Asscioation，1990，85：398-409.

［22］Sklar A.Fonctions de répartition à n dimention set leurs marges［J］.Publication de I’Institut de Statistique de L’Universit-é de Paris，1959（8）：229-231.

［23］韦艳华，张世英.Copula理论及其在金融分析上的应用［M］.北京：清华大学出版社，2008：16-20.

［24］Taylor S J.Modeling Financial Time Series［M］.New York：John Wiley&Sons，1986：16-23.

［25］Nelsen R B.An Introduction to Copulas［M］.New York：Springer，2006：13-14.

［26］Kim，Shephard.Comment of Bayesian analysis of stochastic volatility［J］.Journal of Business and Economics Statistics，1998，12（4）：371-417.

［27］Renate M，Jun Y.BUGS for a Bayesian analysis of stochastic volatility Models［J］.Journal of Econometrics，2000（3）：198-215.

［责任编辑：张兵］

A Study on Risk Contagion from Malaysia Airlines Air Crashes to the Stock Indices of Six Countries（Regions）Based on the Model of Vine Copula-MCMC-SV-T

HAN Chao，YAN Tai-hua

（School of Economics and Business Administration，Chongqing University，Chongqing 400030，China）

The two air crashes of MH370 and MH17 in 2014 caused people anxiety in the world.Anxiety passed from Malaysia Airlines plane crashes to the world conflict，the conflict leads to panics.Panics caused‘long-short’investing by abnormal behavior in stock markets，stimulate stock market risk，the risk spill over from Kuala Lumpur and spread to the world.This paper depicts the volatility processes of six-dimensional marginal stock indices with the model of SV-T，inferred marginal model parameters by using Gibbs sampling method of MCMC algorithm in Bayesian，and described the path diagram of risk contagion of six stock indices in the world in the structure of canonical vine copula，represented four different types of risk contagion by four common types of copula functions，used corresponding value of tau to represent the parameters of corresponding risk contagion，and finally described the risk contagion path and the risk magnitude from Kuala Lumpur to the world.This paper tried to provide a new idea or method for investors to make‘long and short’decision when facing emergencies and for various authorities to grasp the path of crisis contagion，reduce the risk of chain reaction and cut chain of risk contagion.

Malaysia Airlines air crash；crisis contagion；C Vine Copula；MCMC；SV-T

F830.91

A

1007-5097（2016）09-0171-09

2015-10-09

国家自然科学基金项目（71373296）

韩超（1985-），男，重庆人，博士研究生，研究方向：金融工程；严太华（1964-），男，重庆人，教授，博士生导师，研究方向：金融工程。

10.3969/j.issn.1007-5097.2016.09.025