政府创新补贴对零售商双渠道供应链的影响研究

单汨源，刘 超，刘小红

（湖南大学工商管理学院，长沙410082）

政府创新补贴对零售商双渠道供应链的影响研究

单汨源，刘 超，刘小红

（湖南大学工商管理学院，长沙410082）

随着互联网的迅速发展，零售商日益盛行开辟网络销售渠道，零售商双渠道供应链成为一种趋势。文章在政府创新补贴研究基础上构建了由一个制造商和一个零售商组成的零售商双渠道斯塔克伯格博弈模型，研究政府创新补贴对供应链的影响。研究结果表明:政府创新补贴能有效激励制造商进行创新，增加政府创新补贴能拉动供应链整体利润的增长；通过算例对研究问题进行了深入探讨，并给出了政府效用最大化时政府应该设置的创新补贴激励系数。研究结论可为政府制定合理决策提供理论依据和有效参考。

零售商双渠道；斯塔克伯格博弈；政府创新补贴；供应链

一、引言及文献综述

随着我国经济发展进入新常态，以创新谋求发展已经成为企业发展的必由之路，强化技术创新已成为现代企业发展的一股新潮流。然而，我国企业的创新能力相对欠缺，企业创新外部资金渠道比较单一，政府补贴政策有待完善，加强对企业创新投入的激励补偿研究具有重要的现实意义。

国内外一些学者致力于企业R&D补贴政策的研究。Hinloopen（1997）运用两阶段双寡头合作研发模型，验证了研发补贴政策能有效促进研发活动，并指出补贴合作和非合作研发的效果是一样的［1］。Feldman和Link（2001）指出政策对企业技术创新有重要影响，利好政策可以促进企业进行持续创新［2］。鲁文龙（2003）从产业组织理论角度出发分析了国内外两个企业的研发行为，并就最优政府补贴政策进行了探讨，结果表明企业间的技术交流与合作是必要的，政府更倾向于补贴本国企业［3］。生延超（2008）分析了政府创新投入补贴和创新产品补贴对技术联盟创新的影响，结果表明政府补贴能有效激励技术联盟增加创新投入，政府介入的最有效方式是进行创新投入补贴［4］。方海燕和达庆利（2009）建立了考虑产品差异的三阶段双寡头博弈模型，分析了五种R&D策略并得到了相应的政府最优R&D补贴率［5］。孟卫军、张子健（2010）将政府补贴引入供应链产品创新合作中，建立了政府对制造商和供应商合作研发投入进行补贴的博弈模型，对3种不同的情形下对企业的最优研发投入和政府的最优补贴进行了对比分析［6］。彭鸿广、骆建文（2011）构建了由两个竞争的供应商、一个采购商和最终消费者组成的供应链模型，在对供应商总额补

贴、对供应商单位补贴和对消费者单位补贴三种不同情形下，分别考虑了政府研发补贴对供应商研发努力和社会福利的影响［7］。José Gil-Moltó和Poyago-Theotoky（2011）在混合双寡头与纯私企双寡头引入R&D补贴，分析了R&D补贴对技术研发的影响，结果表明研发补贴能促进技术研发的投入并随着技术溢出的增强而增强［8］。Michalsen（2012）在垂直相关产业中考虑政府研发补贴政策，分析结果表明只有当下游市场的集中度高时，政府的最优研发政策是对这些企业提供研发补贴，其他情况下，政府的最优策略是对下游企业提供税收优惠［9］。刘伟（2013）针对上游企业研发投入的产业链结构，从产业链纵向协调和政府补贴两个维度出发，构建4个分阶段的博弈模型，分析了各阶段产业链的纵向协调机制和最优的政府补贴策略［10］。Franco和Gussoni（2014）通过对欧洲7国的实证研究发现，公共补贴对企业开展研发合作有积极影响，在服务业表现特别明显［11］。盛光华和张志远（2015）通过构建多群体演化博弈模型，分析政府补贴方式对企业创新模型选择的影响［12］。吴文清（2015）等针对代际产品的研发合作，综合考虑消费者学习因素和政府补贴因素构建了制造商和供应商的合作研发博弈模型，研究了双方最优的研发投入问题，并给出了政府的研发补贴策略［13］。

通过梳理文献发现，以往文献都集中于单个企业和单渠道供应链的创新补贴研究，考虑双渠道供应链中的政府创新补贴研究相对较少。然而，随着电子商务和互联网在我国的迅猛发展，大型零售企业如苏宁、国美等纷纷开辟电子渠道，加强对零售商双渠道供应链中企业创新投入的激励补偿研究，这具有重要的现实和理论意义。

二、模型假设

本文考虑一条由一个制造商和一个零售商组成的两层供应链，生产和销售单一商品，其中零售商是主导者，并且，零售商在传统渠道的基础上构建了电子渠道。互动过程如下：制造商以批发价格w给零售商供货，零售商以Pt在传统渠道销售产品，以Pe在电子渠道销售产品，消费者根据价格决定购买渠道。

参考陈树桢、熊中楷（2011）构建的线性需求函数［14］，消费者在传统渠道和电子渠道的购买数量分别为:

其中，1代表传统渠道和电子渠道的潜在市场规模；θ为渠道交叉价格弹性系数，当传统渠道产品价格高于电子渠道时，有θPe的消费者选择电子渠道购买产品。

为简化模型且不失一般性，假设零售商的单位分销成本为0，记制造商的单位运营成本为c，制造商通过创新投入可降低产品单位运营成本［15-16］，假设制造商投资c(λ)可将单位运营成本降低λ，且λ＜c并假设c(λ)=λ2。供应链各成员利润可表示为：

制造商利润函数：Πm=(w-c+λ)(1+θw-w)-λ2；

零售商利润函数：Πr=(pt-w)Dt+(pe-w)De；

供应链总利润：Π=Πr+Πm。

本文中各符号定义如下：下标m代表制造商；下标r代表零售商；下标t代表传统渠道；下标e表示电子渠道；下标g表示政府补贴；上标星号表示制造商保留利润最大，例如，Πr*表示制造商保留利润最大时零售商的最优利润，Πrg*表示增加政府创新补贴后在制造商保留利润最大时零售商的最优利润。

三、模型分析

（一）无政府创新补贴的分散决策情形

零售商占主导地位，制造商和零售商进行两阶段Stackelberg博弈：供应商先决定创新投入λ，然后零售商确定批发价w、传统渠道和电子渠道的销售价格Pt/Pe。制造商和零售商独自决策以最大化各自的利润。

零售商的期望利润为Πr=(Pt-w)Dt+(Pe-w)De，对Pt/Pe求导得零售商利润最大化时:

所以Πm(λ)=(w-c+λ)(1+θw-w)-λ2，在零售商确定w下，对λ求导得制造商利润最大化的创新投入为：

此时制造商利润：

以下分两种特殊情况考虑：

（1）当Πm保留利润为零时，零售商给定供应商的批发价格为：，将其带入（1）、（2）、（3）得：

此时可得出：

（2）当Πm保留利润最大时，零售商给定供应商的批发价格为:

*，面对零售商的“低价策略”，制造商只有加大创新投入λ＞λ*降低产品成本才能营利，即当零售商居主导地位时，制造商的保留利润越大其创新投入越小，当制造商保留利润为零时其创新投入越大；强势的零售商往往会压低批发价格以获取较高的利润，这对零售商和整个供应链是有利的，对制造商是不利的。

表1 无政府补贴下分散决策最优解

（二）考虑政府创新补贴的分散决策情形

增加政府补贴后，政府、制造商和零售商之间进行三阶段Stackelberg博弈：政府先决定创新补贴率k，制造商再决定λ，最后零售商确定w、Pt、Pe。

零售商的期望利润为Πr=(Pt-w)Dt+(Pe-w)De，对Pt/Pe求导得零售商利润最大化时：

所以Πm(λ)=(w-c+λ)(1+θw-w)-(1-k)λ2，在零售商确定w下，对λ求导得制造商利润最大化的创新投入为：

此时制造商利润：

（1）当Πm保留利润为零时，零售商给定供应商的批发价格为：

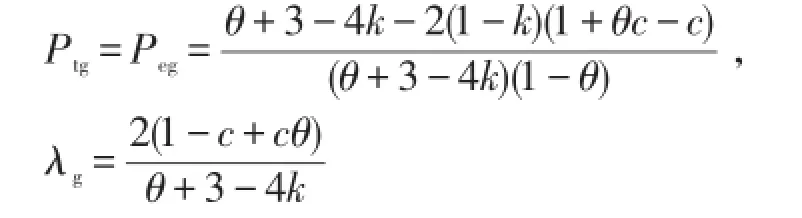
（2）当Πm保留利润最大时，零售商给定供应商的批发价格为:

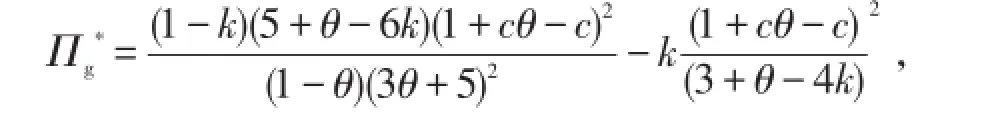
从表2可以看出，政府增加补贴后，强势零售商仍然倾向于”压低批发价格“，此时其利润才是最大的，但是，比较表1和表2，Πrg＞Πr，,增加政府创新补贴后，不管制造商的保留利润处于何种水平，供应链各成员的利润都相应增大，增加政府创新补贴能有效地刺激需求，拉动GDP的增长，并且，制造商的创新投入水平也明显增加，即政府的创新补贴能有效地激励制造商进行创新。

表2 政府最优补贴下分散决策最优解

四、算例分析

为了验证结论的有效性，本文运用Matlab7.0进行数值模拟，通过算例分析政府补贴系数k对零售商双渠道供应链的影响，具体参数的设定参考相关文献，设置的参数满足文章均衡解存在的条件

（一）政府创新补贴对制造商创新投入影响分析

通过模型求解可知，制造商创新投入与产品单位可变成本、政府补贴系数以及渠道交叉价格弹性系数有关，当产品单位成本一定时，制造商创新投入与渠道交叉价格弹性系数正相关，并随着政府补贴系数的增大而增大。

从表1中可以看出，w为正，必须有c∈(1/4，1)、θ∈（0，1），为使仿真结果更直观，θ取0～1，数组计算步长为0.1。

从图1和图2可以看出，制造商创新投入λ随着交叉价格弹性系数θ的增大而增大，而且比较两图可以看出，，制造商的保留利润越小，制造商的创新投入反而越大，当强势零售商压低批发价格时，制造商被迫加大技术创新投入，继而降低成本，增加收入；另外，增加政府补贴后制造商的创新投入明显比无补贴情况下增加（λg＞λ、λg*＞λ*），即政府创新补贴能有效激励制造商进行创新。

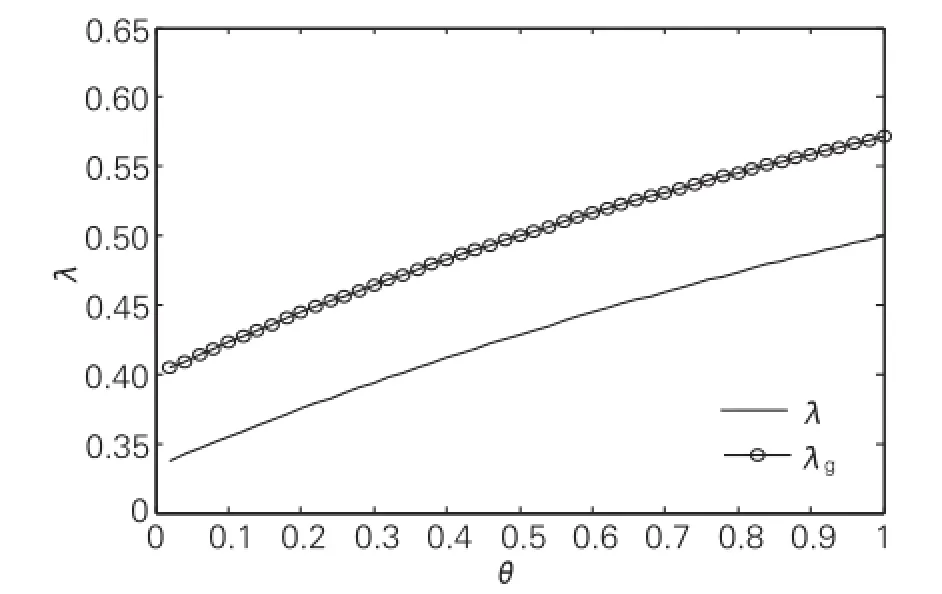
图1 制造商保留利润为零时k在不同θ下对创新投入的影响

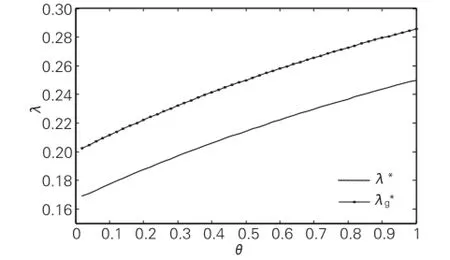
图2 制造商保留利润最大时k在不同θ下对创新投入的影响

（二）政府创新补贴对供应链利润影响分析

保持其余参数不变，θ取0～0.5，数组计算步长为0.05，考察政府补贴系数k对零售商双渠道供应链各成员利润的影响。

从图3和图4可以看出，产品单位成本一定时，不管制造商保留利润为多少，制造商和零售商的利润都随着交叉价格弹性系数θ的增大而增大；增加政府补贴后供应链各成员的利润明显比无补贴情况下增加，增加政府补贴供应链整体利润增加。

图3 制造商保留利润为零时k在不同θ下对供应链利润的影响

图4 制造商保留利润最大时k在不同θ下对供应链利润的影响

（三）政府最优创新补贴率分析

通过模型求解可知，当制造商保留利润为零时政府的最优补贴率为，政府最优创新补贴率与渠道交叉价格弹性系数负相关，为验证结论的有效性，本文进行数值模拟时θ分别取值0.2、0.3、0.4、0.5、0.6。

从表3可以看出，制造商保留利润为零时，政府的效用随着θ的增大而增大，但是，政府的最优补贴率随着θ的增大而减小，当θ分别取值0.2、0.3、0.4、0.5、0.6时政府效用随着k先增大后减小，当k依次为0.1、0.09、0.08、0.06、0.05时，政府效用取到最大值。

当制造商保留利润为最大时，通过模型求解可以得到政府的最优补贴率k*=1/3，保持参数不变，利用Matlab计算出的结果见表4所列。

从模拟结果可以看出，制造商保留利润最大时，政府的效用仍然随着θ的增大而增大，并且，不管θ处于何种水平，政府效用随着k先增大后减小，当k取0.33时政府的效用达到最大值。

表4 制造商保留利润最大时不同交叉价格弹性系数θ下政府的最优补贴率分析

五、结论

本文通过以上研究构建了零售商双渠道Stackelberg博弈模型，分析了政府补贴系数对供应链的影响，最后通过数值算例对结论进行了验证。研究结果表明，零售商双渠道供应链中占有优势地位的零售商往往会压低批发价格和产品零售价格以获取较大的利润，这种“低价策略”对零售商和整个供应链是有利的，但是对制造商却是不利的。制造商为了营利被迫增加创新投入以降低产品成本，增加政府补贴后，并不会改变零售商压低批发价格获得较高利润的现象。此外，从整个供应链的角度来看，政府创新补贴不仅能促使制造商加大创新投入，还能提高供应链各成员利润，拉动供应链整体利润的增长。最后，本文给出了政府效用最大化时政府应该设置的补贴激励系数，当制造商保留利润为零时，创新补贴系数与交叉价格弹系数负相关，当制造商保留利润最大时，创新补贴系数为定值。研究结论为政府鼓励企业创新、提供政府补贴提供了实用性的理论依据。

［1］Hinloopen J.Subsidizing cooperative and noncooperative R&D in duopoly with spillovers［J］.Journal of Economics，1997，66（2）：151-175.

［2］Feldman M P，Link A N.Innovation Policy in the Knowledge-Based Economy for Public Policy［M］.Amsterdam：Cluwer Academic Publisher，2001：73-74.

［3］鲁文龙，陈宏民.R&D合作与政府最优政策博弈分析［J］.中国管理科学，2003，11（1）：60-62.

［4］生延超.创新投入补贴还是创新产品补贴：技术联盟的政府策略选择［J］.中国管理科学，2008（6）：184-192.

［5］方海燕，达庆利.基于差异产品的政府最优R&D补贴策略研究［J］.中国管理科学，2009（3）：166-172.

［6］孟卫军，张子健.供应链企业间产品创新合作下的政府补贴策略［J］.系统工程学报，2010（3）：359-364.

［7］彭鸿广，骆建文.激励供应商R&D努力的最优补贴策略研究［J］.工业工程与管理，2011（5）：41-47.

［8］José Gil-Moltó M.Poyago-Theotoky J.R&D Subsidies，spillovers，and privatization in mixed markets［J］.Southern Economic Journal，2011，78（1）：233-255.

［9］Anita Michalsen.R&D policy in a vertically related industry［J］.Economics of Innovation&New Technology，2012，21（8）：737-751.

［10］张泽华，刘伟.上游企业R&D投入的纵向协调机制与政府补贴策略研究［J］.科技进步与对策，2013（17）：102-107.

［11］Franco C，Gussoni M.The role of firm and national level factors in fostering R&D cooperation：a cross country comparison［J］.Journal of Technology Transfer，2014，39（6）：945-976.

［12］盛光华，张志远.补贴方式对创新模式选择影响的演化博弈研究［J］.管理科学学报，2015（9）：34-45.

［13］吴文清，刘晓英，赵黎明.消费者学习与政府补贴下的制造商-供应商合作研发［J］.系统工程，2015（10）：1-7.

［14］陈树桢，熊中楷，李根道，等.考虑创新补偿的双渠道供应链协调机制研究［J］.管理工程学报，2011，25（2）：45-52.

［15］Gilbert S M，Cvsa V.Strategic commitment to price to stimulate downstream innovation in a supply chain［J］.European Journal of Operational Research，2003，150（3）：617-639.

［16］Cho R K，Gerchak Y.Supply chain coodination with downstream operating costs：Coordination and investment to improve downstream operating efficiency［J］.European Journal of Operational Research，2005，162（3）：762-772.

［责任编辑：余志虎］

Research on the Effect of Government Innovation Subsidy on Retailer’s Dual Channel Supply Chain

SHAN Mi-yuan，LIU Chao，LIU Xiao-hong
（School of Business and Administration，Hunan University，Changsha 410082，China）

With the robust development of Internet，online sales has become the new fashion which together with retailer，this dual channel sailing model has been a kind of trend.In this paper，a stackelberg game model of dual supply by manufacturer and retailer was generated on the basis of reasearch on goverment inovation subsidy.We aimed at discussing the effect of government inovation subsidy on supply chain.Our observation showed that：the government innovation subsidies can effectively motivate the manufacturer’s creativity.And increasing the subsidies can promote the growth of the benifits of the whole supply chain.Finally，a numerical example was given to thoroughly discuss the research questions and a optimized coefficient of government inovation subsidy was given to help the government to make a more reasonable decision as a theoretical basis and practical reference.

retailer’s dual channel；stackelberg game theory；government innovation subsidy；supply chain

F274

A

1007-5097（2016）09-0120-05

2016-04-05

国家自然科学基金项目（70971036）；国家社会科学基金后期资助项目（13FGL005）

单汨源（1962－），男，湖南岳阳人，教授，博士生导师，研究方向：电子商务，运营管理，信息管理；刘超（1990－），男，湖南湘潭人，硕士研究生，研究方向：运营管理，物流与供应链管理；刘小红（1980－），女，湖南益阳人，博士研究生，研究方向：系统优化与运作管理。