基于遗传算法的自动化立体仓库货物配载研究

姚琪， 周乐， 陈宝生， 何明凯

(国网吴忠供电公司，宁夏 吴忠 751100)



基于遗传算法的自动化立体仓库货物配载研究

姚琪， 周乐， 陈宝生， 何明凯

(国网吴忠供电公司，宁夏 吴忠 751100)

针对自动化立体仓库货物仓位的配载问题建立了一个多目标数学模型。首先根据立体仓库货位分配的原则与策略建立合理的货架重心模型与目标函数，其次根据货物出/入库的高效性建立货物存取效率最优模型。采用基于种群操作的遗传算法求解最优配载结果，通过优化遗传算法，并利用MATLAB程序设计对实际货架的货位分配仿真实例进行计算求解。结果表明：采用改进的遗传算法对货位进行优化分配，可降低货架的重心目标函数值及堆垛机访问时间目标值，增强了货架的稳定性，提升了堆垛机的效率，有效的提高仓库性能。

自动化立体仓库；货位分配；多目标优化；遗传算法；MATLAB仿真

0 引 言

自动化立体仓库(AS/RS)是现代物流系统中迅速发展的一个重要组成部分。如何合理规划和设计自动化仓库，实现自动化仓库的高效运行，已经成为重要的研究课题，是自动化立体仓库中货物分配方面首先需要考虑的问题。

自动化立体仓库的效率主要取决于库区和货位的分配策略，良好的优化策略可以大大提高货物周转效率，方便盘点及移库。货位分配制约着立体仓库的整体性能的提升，研究货位分配算法具有重要的意义[2]。

本文结合立体仓库的构造模型，根据货位分配的原则和策略建立了合理的货位分配数学模型，重点研究遗传算法在货物分配中的使用。利用遗传算法进行多目标优化求解，得到货物分配的方法。

1 自动化立体仓库

1.1 立体仓库的组成结构

自动化立体仓库(AS/RS)是由立体货架、有轨巷道堆垛机、出入库托盘输送机系统、尺寸检测条码阅读系统、通讯系统、自动控制系统、计算机监控系统、计算机管理系统以及其他如电线电缆桥架配电柜、托盘、调节平台、钢结构平台等辅助设备组成的复杂的自动化系统[3]。典型的自动化立体仓库结构图如图1所示。

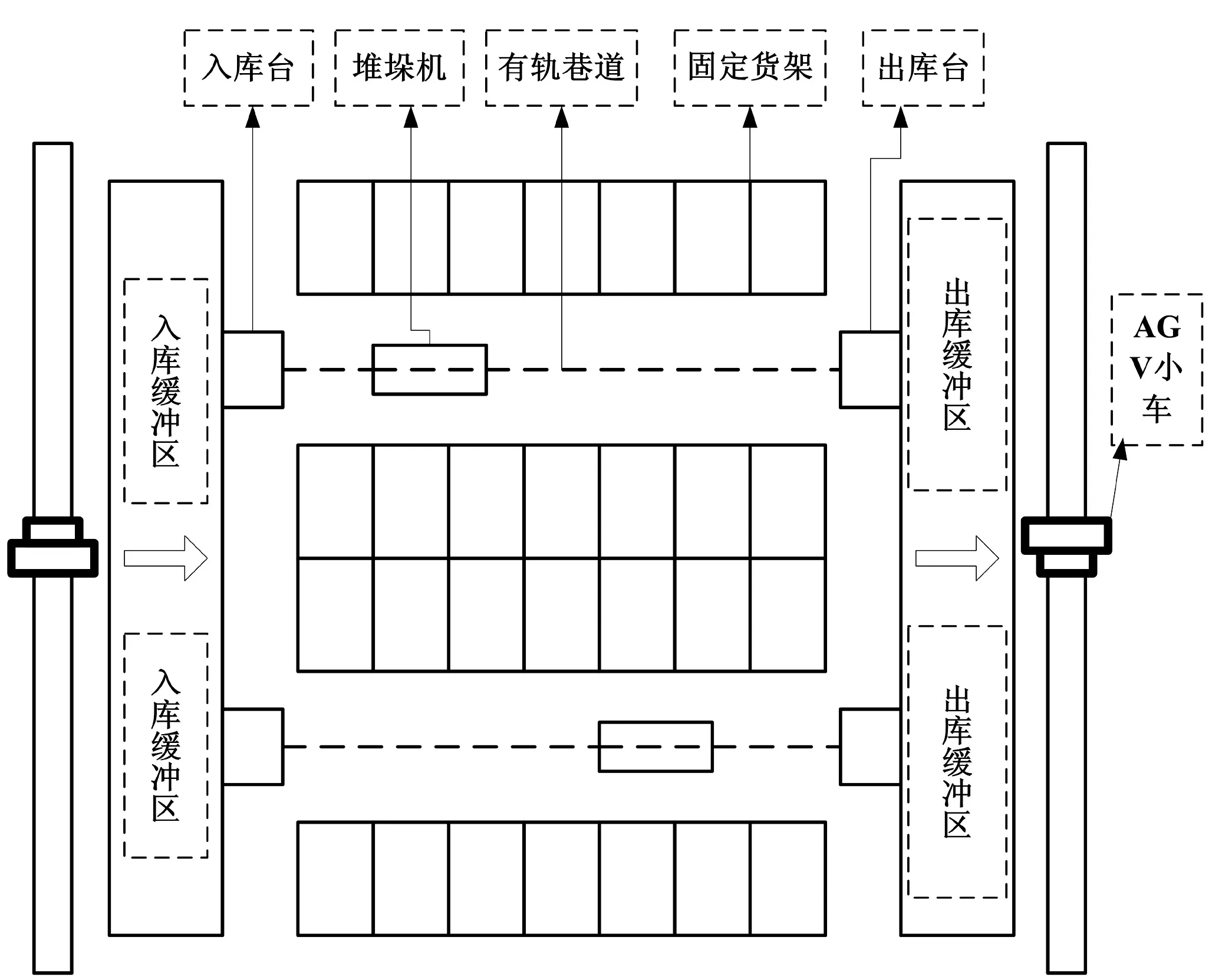
图1 典型的自动化立体仓库结构图

1.2 立体仓库货位分配原则与策略

自动化立体仓库货位分配主要考虑的因素有货架的稳定性、货物出入库的效率、保证货物的质量、安全经济等。在仓储管理中，首先要保证立体仓库的稳定性，其次，充分发挥仓储设施和设备的作用，可以提高仓储设施的劳动生产率。一般来说，货位分配需要遵循以下的几个原则[4]：货架受力均匀和稳定性原则；分巷道存放原则；就近出/入库原则；产品相关性原则；先入先出原则。

2 系统数学模型建立

2.1 系统参数

自动化立体仓库系统由模拟立体仓库和出入库输送设备组成[5-6]。立体仓库为4层×6列立体货架，仓位编码规定：从左到右，从下到上。相关参数如表1所示。

表1 自动化立体仓库的相关参数

2.2 数学模型

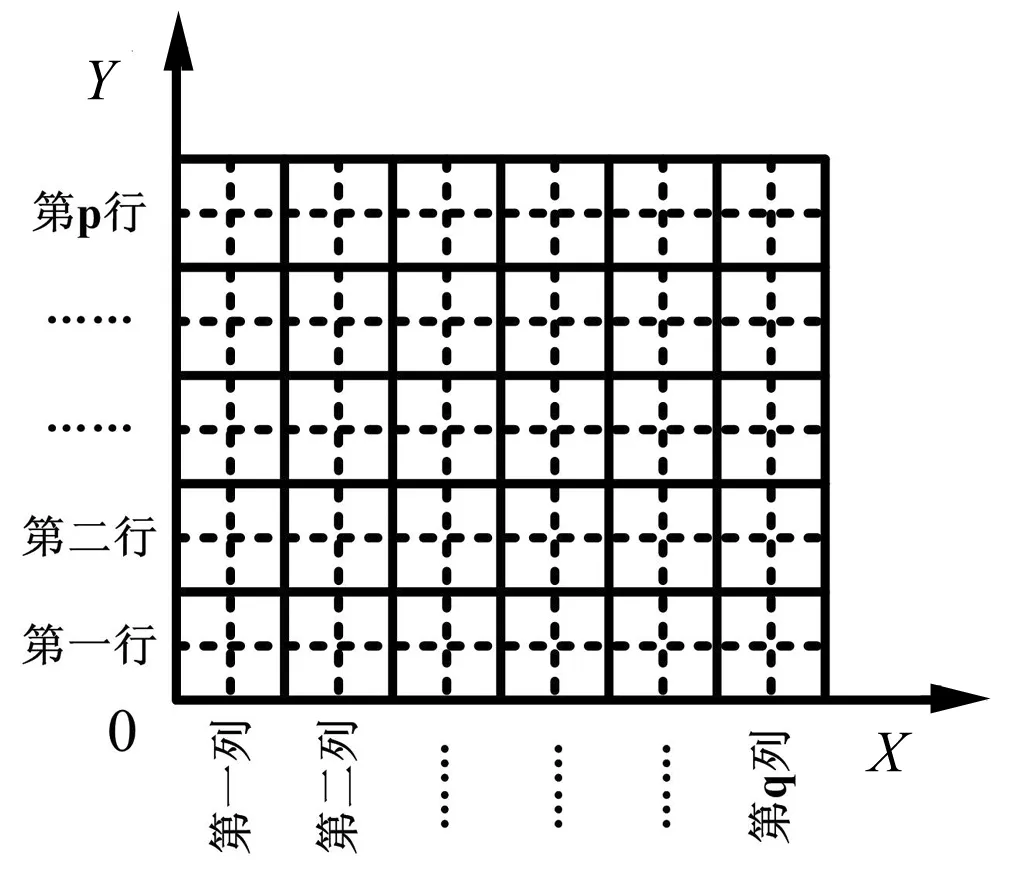
图2 实际货位与数学坐标对照示意图

假设某个货架一共有p层q列，将距离出、入库最近的列记为第一列，最低层设为第一层，将处于第i列第j层的货位坐标记为(i,j),i=1,2,3,…,q；j=1,2,3,…,p。设每个货位的长记为L，每个货位的高记为H。在图2中，虚线的交点对应着每一个货位的几何重心。设堆垛机的水平运行速度为VX,垂直速度设为VY。VX、VY分别为各自运行方向上单位长度(垂直方向为H，水平方向为L)与单位运行时间之比。

立体仓库货位分配的关键有两方面：一是货架的安全性，其受力的均匀性与稳定性；二是出/入库的时间能够尽量缩短，货物出/入库的效率要高。从这两个方面出发来建立立体仓库货位数学模型[7]。

3 仓库模型建立与求解

3.1 建立货架的重心稳定模型

对于任意货位，虚线位置是其几何重心，易得到对于货位(i,j)重心位置为((i﹣0.5)L,(j﹣0.5)H)。整个货架的重心坐标可以表示为：

(1)

其中Gij是相应货位上货物的重量，Gx为重心X轴坐标，GY为重心Y轴坐标。

为了满足货架的稳定性，在垂直方向上要求重心不能太高，即重心Y坐标要尽量小，从水平方向上要求重心X坐标尽量落在货架几何中轴线，于是建立重心稳定数学模型如公式(2)、(3)所示：

(2)

(3)

由式(2)、(3)可见，货架重心模型包含了两个目标函数，为了简化，通过权衡重心X坐标和Y坐标对整个货架稳定的重要性，分别赋予公式(2)、(3)一个加权因子，可得公式(4)：

(4)

3.2 建立存取效率最优模型

为了建立存取效率最优模型，做以下假设[8-9]：

① 所涉及的货物种类，出/入库频率已知；

② 假设其出/入库站台在货架的同一端。

由于存取货物所花费的总时间是所有货物的访问时间之和，设位于(i,j)的货物出入库频率为fij，每次取该货物所花费的时间为tij，令eij=fij×tij，可得存取所费时间的数学模型为：

(5)

其中tij为堆垛机从(0，0)处移动到(i,j)处的时间，且有：

(6)

综上所述可知，货物分配的数学模型由式(4)和式(5)组成。

3.3 遗传算法求解模型

本文选择遗传算法作为求解货位分配优化问题的算法[10-11]。通过修正遗传算法使其应用于货位分配建模的求解[12]，具体步骤如下：

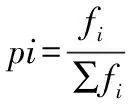
(2) 改进交叉策略:对于p层q列的货架，一共有p×q个货位，所以货物编号从1号到p×q号。为了克服种群只在单一目标上进化，必须引入限制交叉策略。

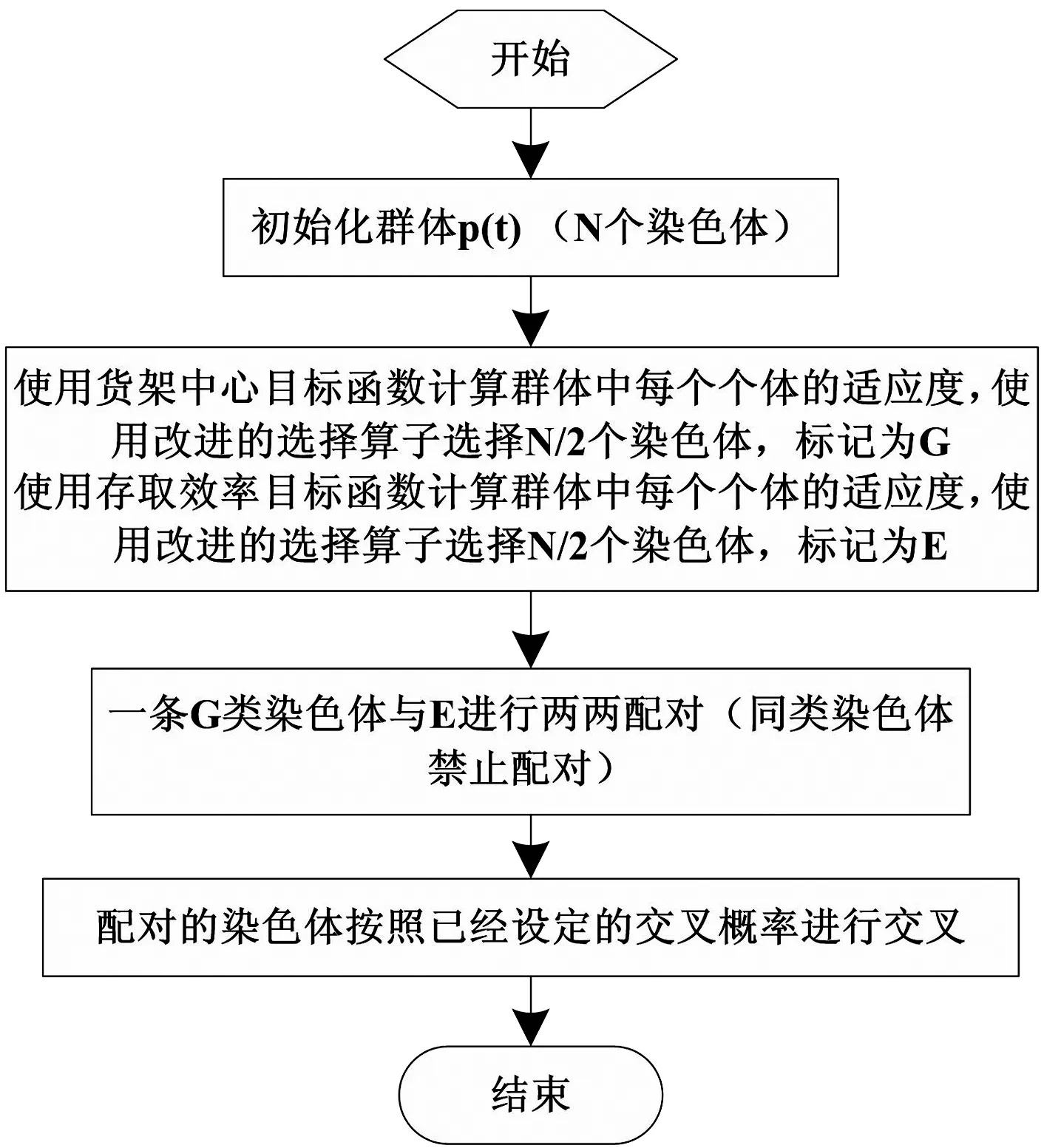
图3 限制交叉策略流程图

首先初始化一个数目为N的群体P(t)，将其分为两个种群，个数都为2/N个，分别使用改进的重心选择操作数和改进的效率选择操作数作用于两个群体，对得到的两个下一代子种群设定不同的标签，禁止子种群内部进行交叉，让这两个子种群之间进行两两随机配对，具体流程如图3所示。

4 遗传算法货位分配仿真实例

4.1 仿真实例

立体仓库货架为4层6列的形式。其中货架长L=0.18 m，高度H=0.12 m。堆垛机的运动参数为VX=0.5 m/s，VY=0.5 m/s(所用为最大速度)。为了使模型理想化，设堆垛机的加速、减速耗时为0。对货叉伸缩所耗时间忽略不计。货架的货位编号如表2所示。未经优化前，将货物放入与之编号一样的货位中。

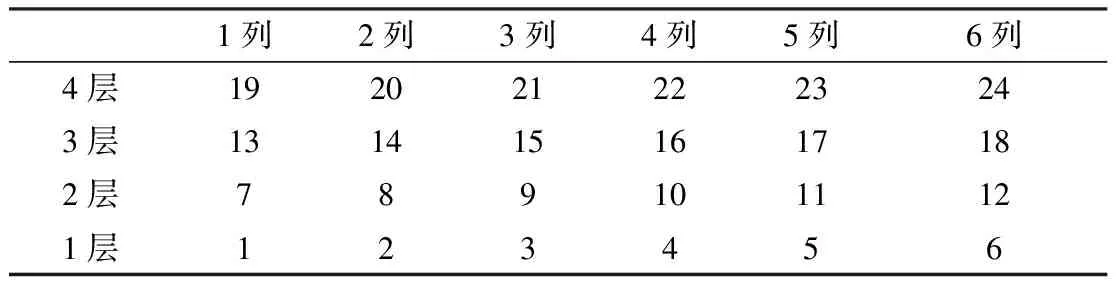
表2 立体仓库货位编号

假设待存入的24件托盘货物的质量和出入库频率表及其货物编号如表3所示。

表3 托盘货物的质量和出入库频率

4.2 仿真求解

根据之前算法的研究，可得出具体操作过程如下：

(1) 编码：根据货位的特点，首先建立一个4*6的矩阵，如果矩阵的第i行第j列位置的元素为m，则表示编号为m的货物放在货架的第(p+1-i)层第j列上。

(2) 确定适应度评价方法：由式(4)，(5)知该函数的优化目标是要求解函数的最小值，因此函数的值越大其遗传到下一代的概率应该越小，故设计适应度函数如公式(7)、(8)所示：

(7)

(8)

式中fg对应于货架重心位置的适应度，fe对应于存取效率的适应度；G和E是个体对应的子函数目标值，Gmax和Emax是进化到最近若干代中目标函数的最大值。

(4) 相关参数设定：① 压力操作数μ取0.25。② 按照流程，选择N/2个染色体用于交叉操作，N(种群个数)取100。③ 交叉运算中取pc=0.4～0.99。 ④变异概率取0.001～0.1。⑤最大进化代数T=20～100。

(5) 算法结束后，根据最终得到的群体，继续计算每个染色体所对应的两个目标函数值，通过比较选择两方面性能都较优的染色体作为最优解。

4.3 仿真结果分析

编写MATLAB程序进行仿真，初始化种群数目为100，最大进化代数100，交叉概率0.9，变异概率为0.099。依据上述算法进行编程求解，最终得出相应的仿真结果。

以2号个体为例，在优化前，其经过随机货物分配后货物摆放情况如下：

进化后货物分配情况则为：

再分别任意选用59号、88号、93号参与运算，也将分别得出其优化后的重心目标函数值和效率目标函数值。则优化前后目标函数值对比情况如表4所示。

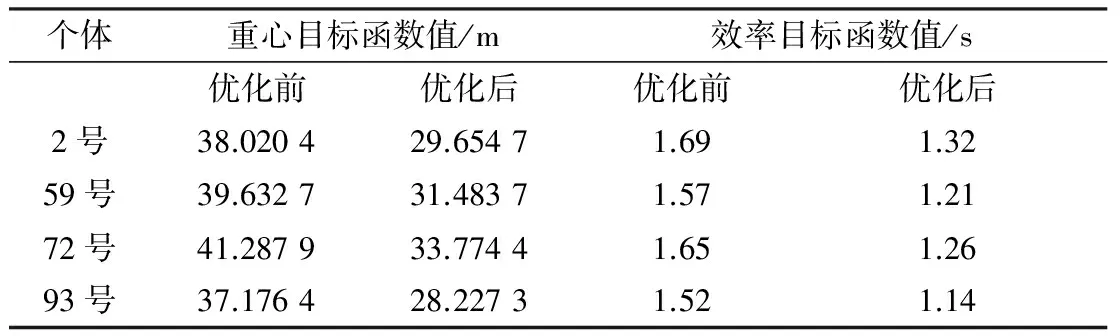
表4 优化前后目标函数值对比

用59号72号93号个体参与运算时，优化后相应的货物分配方案分别如下所示：

结合表3、4中的数据可以得出：采用改进的遗传算法后，货架的重心目标函数值降低，货架的稳定性增强；同时，堆垛机的访问时间目标值降低了，堆垛机的效率得到了提升。由此可见，使用改进的遗传算法对货位进行优化分配可以取得较好的效果。

5 结束语

结合立体仓库的构造模型，根据立体仓库货位分配的几种原则与策略建立了合理的货位分配数学模型，运用遗传算法求解多目标函数的最优解。使用基于Pareto最优解的改进遗传算法进行算法设计，并使用MATLAB语言进行程序设计，对实际一个4*6(即4层6列货架)货架的货位分配进行仿真计算。通过对比优化前后仓库的性能发现，其算法可降低货架的重心目标函数值及堆垛机访问时间目标值，增强了货架的稳定性，提升了堆垛机的效率，仓库的性能得到了有效的提升。

[1] 陈月婷,何芳.基于遗传算法的自动化立体仓库的货位优化分配[J].物流科技, 2008,32(1):2-5.

[2] 张建奇,李墨翰,张建锋.自动化立体仓库控制系统设计[J].自动化仪表,2012,56(1):24-28.

[3] 陈月婷,何芳.基于改进粒子群算法的立体仓库货位分配优化[J].计算机工程与应用,2008,45(11):35-39.

[4] 王强.基于遗传算法的自动化立体仓库出入库货位分配优化研究[J].物流工程与管理,2012,34(3):11-16.

[5] 陈厚孙.自动化立体仓库出入库货位分配优化研究[D].湖北:武汉大学,2011.

[6] 孙嘉炜.立体仓库出入库货位优化模型与算法研究[D].沈阳:东北大学,2013.

[7] 马清悦,张纪会,宋晓鹏,等. 基于启发式算法的自动化立体仓库拣货路径优化研究[J].青岛大学学报,2012,27(3):34-39.

[8] RAO S S,ADIL G K．A mathematical model for optimal partitions of warehouse storage space based on turnover density.[J].Proceedings of the 5thAsia Modelling Symposium,2011(3):24-29.

[9] KOFLER M．Modeling and optimizing storage assignment in a steel slab yard[J].Proceedings of the 4thIEEE International Symposium on Logistics and Industrial Informatics, 2011(6):46-51.

[10] 张学敏,张航.基于改进蚁群算法的最短路径问题研究[J].控制理论与应用,2009,7(28):35-39.

[11] 熊芳敏，芩宇森，曾碧卿. 运用蚁群算法解决物流中心拣货路径问题[J].华南师范大学学报,2010,55(2):56-61.

[12] 庞龙, 陆金桂. 基于蚁群遗传算法的自动化立体仓库拣选路径优化[J].计算机工程与科学,2012,40(3):45-50.

Research on Cargo Stowage in the Automatic Stereoscopic Warehouse Based on Genetic Algorithm

Yao Qi，Zhou Le，Chen Baosheng，He Mingkai

(State Grid Wuzhong Power Supply Company, Wuzhong, Ningxia 751100, China)

With respect to cargo position stowage in the automatic stereoscopic warehouse, we build up a multi-objective mathematical model. First, we establish a reasonable model for the shelf gravity center and objective function according to the principle and strategy of position assignment in the stereoscopic warehouse. Second, we establish a model for optimal goods access efficiency in the principle of high in and out-warehousing efficiency. An optimal stowage result is achieved by means of genetic algorithm based on population operation. Through optimization of genetic algorithm and Matlab programming, we calculate simulation examples for position assignment in actual shelve. The results show that by adopting the improved genetic algorithm to optimize the allocation of cargo space, we can reduce the objective function value of the gravity center of the shelves as well as the target value of stacker access time, thus enhancing shelf stability, raising stacker efficiency and improving warehouse performance.

automatic stereoscopic warehouse; storage allocation; multi-objective optimization;genetic algorithm; MATLAB simulation

10.3969/j.issn.1000-3886.2016.04.015

TP273

A

1000-3886(2016)04-0045-04

姚琪(1986-)，男，宁夏吴忠人，中级工程师，工学硕士学位，主要从事电力系统自动化工作，研究方向电力系统保护与自动控制。 周乐(1990-)，男，宁夏吴忠人，助理工程师，工学学士学位，主要从事电力系统自动化工作，研究方向电力系统保护与自动控制。 陈宝生(1986-)，男，辽宁阜新人，高级技师，工学双学士学位，主要从事电力系统自动化工作，研究方向自动控制与应用。 何明凯(1987-)，男，宁夏盐池人，技师，工学学士学位，主要从事电气自动化工作，研究方向自动控制。

定稿日期: 2015-12-30