带内树状支承柱单层球壳的优化分析

高健, 高轩能

(华侨大学 土木工程学院， 福建 厦门 361021)



带内树状支承柱单层球壳的优化分析

高健, 高轩能

(华侨大学 土木工程学院， 福建 厦门 361021)

采用遗传算法和拟满应力法，以结构总质量为目标函数，杆件截面积为离散变量，对某带内树状支承柱单层球壳实际工程进行优化分析.通过在强度、杆件稳定和刚度等约束条件下，对优化结果的比较分析及对优化后的球壳结构的几何非线性全过程整体稳定性分析，使设计方案更加经济合理.算例结果表明:刚度条件对球壳结构优化起控制作用，杆件稳定和结构整体稳定性不可忽视；对带内树状支承柱单层球壳结构，要使结构设计方案经济合理，进行优化分析和方案比较是必要的.

单层球壳； 遗传算法； 树状支承柱； 优化分析

网壳结构由于结构受力合理、造型美观等特点而广泛应用于各类大型公共建筑当中[1].在保证网壳结构使用功能和满足设计指标的前提下，对网壳进行优化一直是结构设计和研究中需要解决的问题[2].常规大跨球壳结构通过建立自重最小或造价最低的目标函数，调整结构自身参数来实现结构优化.张年文等[3]以杆件截面积为设计变量对网壳进行了优化设计，对比不考虑几何非线性和考虑几何非线性的优化结果，指出网壳设计中考虑几何非线性的重要性.尚凌云等[4]考虑了两种球节点体积对网壳造价的影响并给出优化结果.王法武等[5]在文献[3-4]的基础上，增加了整体稳定等约束条件，对杆件截面进行优化.文献[6-8]围绕网壳的矢高、跨度、网格密度等因素对结构优化结果的影响进行了比较分析，给出结构和构件选型建议.文献[9-12]则利用BP神经网络建立了网壳跨度、矢跨比与用钢量最少的网壳选型的映射关系，简化了结构杆件种类.但上述方法和结论难以直接应用于内设支柱的网壳，而实际工程中这类结构并不鲜见.因此，本文对内设支柱的大跨网壳结构进行优化研究，分析影响结构性能和经济性指标的控制因素，提出结构优化设计建议.

1 工程概况

某创意产业园多功能厅屋盖为扁圆体球面网壳结构屋顶，直径70.8 m，弦高22 m，外檐口边距地3 m，球面屋顶表面积7 000 m2，采用全玻璃屋面.球面屋盖采用单层网壳结构，网壳外圈周边设置V型柱支承，内部设置两圈树状钢结构柱(共24根，内圈6根，外圈18根)支承.V型柱底部与基础铰接，柱顶与网壳铰接；树状支柱底部刚接，柱顶与网壳铰接.球壳屋顶,如图1所示.

(a) 室内效果图 (b) 整体效果图图1 多功能厅的球壳屋顶效果图Fig.1 Spherical shell roof

钢网壳采用钢管(材质为Q235B)相贯线焊接连接，所有杆件均为热轧无缝钢管与电焊钢管.网壳结点采用钢管空间相贯连接方式连接.网壳结构的设计图纸中，主肋杆、最外圈的环向杆件选用钢管截面为φ219×10；最内圈杆件选用钢管截面为φ273×10；树状钢结构柱柱身选用钢管截面为φ600×10；柱身上部树枝状的杆件选用钢管截面为φ245×8；最内圈及最外圈的环向杆件、非主肋的径向杆件、斜杆以及V型柱选用钢管截面为φ219×8.网壳结构各部分组成和整体结构示意图，如图2所示.

图2 球壳结构组成及整体模型图Fig.2 Components and overall model of spherical shell

2 带内支承柱单层球壳的优化分析

2.1 结构优化方法的选择

根据设计变量的不同,结构优化方法可以分为连续变量优化设计法和离散变量优化设计法.已有的研究表明，采用连续变量优化设计法对网壳结构求最优解，再圆整得到离散解，通常会产生较大偏差，其优化结果并不理想[12-13].同时，由于结构构件截面选材的离散性，网壳结构的优化宜采用离散变量优化设计法，包括一维搜索算法和遗传算法.

一维搜索算法的基本思想是将设计变量的离散集按照升序进行排列，保证目标函数是设计变量的单调递增函数、约束函数是设计变量的单调递减函数的前提下，依次将设计变量离散集中的截面参数代入到约束条件当中，若约束条件不满足，则将排序中的下一个截面参数继续代入到约束条件当中，直至所有约束条件都得到满足为止.此逻辑下找到的第一组满足要求的截面参数，即为结构优化的最优解.其优点在于优化计算收敛速度快，但是一次只能针对单个变量进行计算，不适用于优化设计中同时存在多个变量的情况.遗传算法将自然遗传优选的过程抽象剥离出来，以优化计算中的多种变量构成一组染色体，在对多种变量分别赋予离散的变量值后，形成多组染色体组成的初始母体种群，在此基础上进行选择、交叉、变异等运算，并通过适应度函数评定染色体的优劣程度，保留适应度大的染色体，淘汰适应度小的染色体，反复循环该过程，得到结构优化的最优解.

对于设置内支承树状支柱的钢球壳结构，优化的设计变量并不单一，一维搜索法难以满足要求，故采用遗传算法.首先，通过通用有限元ANSYS进行优化设计计算，在优化过程中，加入强度、单杆稳定、刚度等约束条件；然后，进行球壳的整体稳定性校核.为对比优化效果，应用钢结构设计专业软件3D3S中的拟满应力法，对球壳结构进行优化，并对结果进行比较分析.

2.2 优化设计数学模型的建立

目标函数是以单层网壳总质量为目标建立的函数，即

(1)

式(1)中:W为结构所有杆件的总质量(kg)；ρi为第i根杆件材料的密度，杆件为钢材，取为7.85 kg·m-3；Ai为第i根杆件的横截面积(m2)；Li为第i根杆件的实际长度(m).

按照总用钢量最少的优化目标，拟定5个设计变量分别为：除最内圈和最外圈外的环向杆件、非主肋的径向杆件、斜杆及V型柱钢管的截面面积(Aa)；主肋杆、最外圈环向杆件钢管的截面面积(Ab)；最内圈环向杆件钢管的截面面积(Ac)；树状钢结构柱柱身钢管的截面面积(Ad)；树枝状部分的杆件钢管截面面积(Ae).每组构件截面面积为离散化变量，分布情况如图3所示.其取值范围根据3D3S截面库中对应类型的钢管截面信息确定.

图3 杆件分布图Fig.3 Member distribution

约束条件：结构和构件应满足我国设计规范JGJ 7-2010《空间网格结构技术规程》[14]的要求.

刚度条件：单层网壳屋盖结构的最大挠度为其短跨方向的1/400，即Δmax≤2R/400=70 800/400=177 mm.杆件长细比：受压杆件的容许长细比≤150；承受静载的受拉杆件容许长细比≤300；承受动载的受拉杆件容许长细比≤250.

杆件强度约束条件为

(2)

式(2)中:Ni为第i根杆件的轴力；Mi为第i根杆件上的最大弯矩；Ai为第i根杆件的截面面积；Wi为第i根杆件的抗弯模量；γ为塑性发展系数，所有截面均为圆钢管，γ取1.15.

平面内压弯杆稳定性约束条件为

(3)

平面外压弯杆稳定性约束条件为

(4)

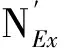
单层球壳除应满足构件稳定条件外，还应满足结构的整体稳定性.鉴于仅对优化结果进行整体稳定性校核，文中按弹性理论进行整体稳定全过程分析.将求得的临界荷载pcr除以安全系数K，即得到单层球壳的整体稳定承载力(标准值)，并据此验证结构的整体稳定性是否满足设计要求.

2.3 优化结果及分析

为了便于比较分析，设工程原设计为方案1，优化后为方案2，移除网壳内部树状支柱重新调整网壳杆件截面并优化的结构为方案3.各设计方案的球壳杆件截面尺寸通过3D3S建模计算确定，计Pa算考虑的荷载包括恒载DL(取值为1.2kPa)、活载LL(取值为0.5kPa)、以朝向网壳门洞为正向且相互正交的4个方向的风荷载WL1-WL4(基本风压取0.45kPa)、地震荷载EL及温度作用TL(±30 ℃)等，共有23种工况组合.

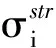
表1 原设计方案1计算结果

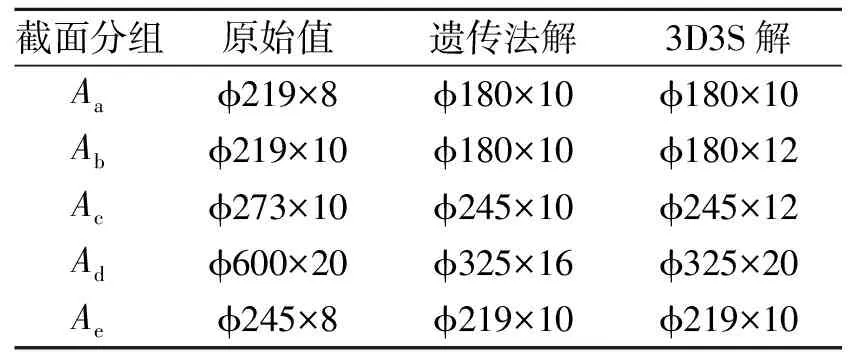
表2 方案1的杆件截面优化表

按上述方法对方案1的单层球壳进行优化计算，具体过程如下：1) 应用3D3S生成ANSYS下的网壳建模命令流，导入到ANSYS当中进行优化计算；2) 建立备选钢管截面型号表，并将截面的型号赋值于优化设计的数组中；3) 应用遗传算法进行迭代计算，将原设计方案中Aa～Ae截面替换为优选截面；4) 在3D3S中，利用拟满应力法进行网壳杆件截面优化，得到另一组杆件优选截面.杆件优化结果，如表2所示.对优化后的球壳(方案2)重新计算，得到的结构最不利工况计算结果和总质量优化率(与原设计球壳总质量相比的总质量减少比率)， 如表3所示.表3中：η为优化率.由表3可知：采用遗传算法优化计算后，带内

表3 方案2的计算结果

图4 杆件轴向变形分布(方案2)Fig.4 Axial deformation distribution of member (scheme 2)

树状支承球壳的总质量减少了20.44 t，优化率为4.50%；而采用3D3S的优化率为3.85%，效果明显.在进行遗传算法优化计算时，由于ANSYS无法直接得到杆件的稳定计算结果，需要通过提取相应杆件编号的内力，代入式(3)和式(4)验算杆件的稳定性.以总质量最少为目标函数的单层球壳优化设计，结构的最大挠度和杆件的稳定承载力是主要控制因素.

最大杆件变形对应工况的球壳整体变形分布,如图4所示.由图4可知：带内树状支承球壳的杆件轴向最大压缩量为2.38 mm，最大拉伸量为1.21 mm，且压缩变形主要集中在开设门洞区域的5～6环杆件上.

表4 去除内支承柱球壳的杆件截面优化表

为了进一步优化设计和比较分析，取消原设计球壳内部设置的树枝支柱，对球壳结构重新进行建模，并按上述过程进行优化计算.相应的杆件优化结果，如表4所示.结构最不利工况计算结果和总质量优化率,如表5所示.最大杆件变形对应工况的球壳整体变形分布，如图5所示.

由表4可知：相比原设计，优化得到的球壳杆件截面，部分有增大，这将导致网壳结构总质量的增加.这是因为去除内树状支承柱后，球壳结构由周边+内多点支承体系改变为周边支承网壳，屋盖荷载由支柱和球壳共同承担变为由网壳单独承担.由表5可知：尽管网壳杆件截面有所增大，但相比原设计方案，采用遗传算法和3D3S优化后的球壳结构总质量优化率仍然可以达到1.20%和0.83%.

表5 方案3的计算结果

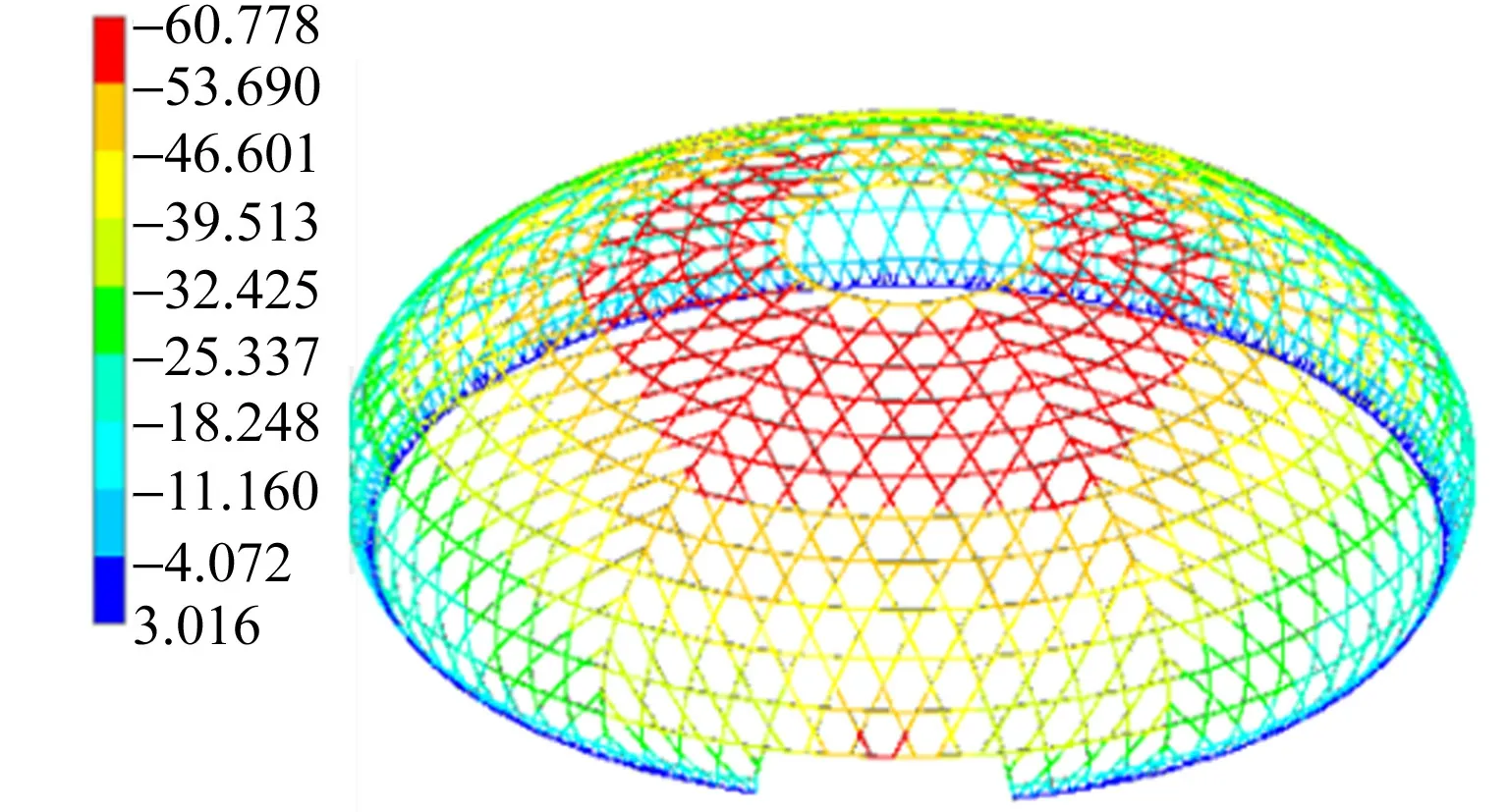
图5 杆件轴向变形分布(方案3)Fig.5 Axial deformation distribution of member (scheme 3)

由图5可知：去除内树状支承柱后的球壳杆件变形程度相比方案2有明显增大，网壳整体变形分布不如带内树状支承柱时均匀.杆件轴向最大压缩量达到6.08 mm，最大拉伸量为0.30 mm，压杆的分布区域从第一环延伸至6～7环.由此可知，内树状支承柱使网壳杆件的受力均匀合理.因此，在构件选型追求简洁的实际工程中，内树状支承柱的采用有利于材料的充分使用，但同时也将减小结构空间内的使用面积.

3 优化后结构的整体稳定分析

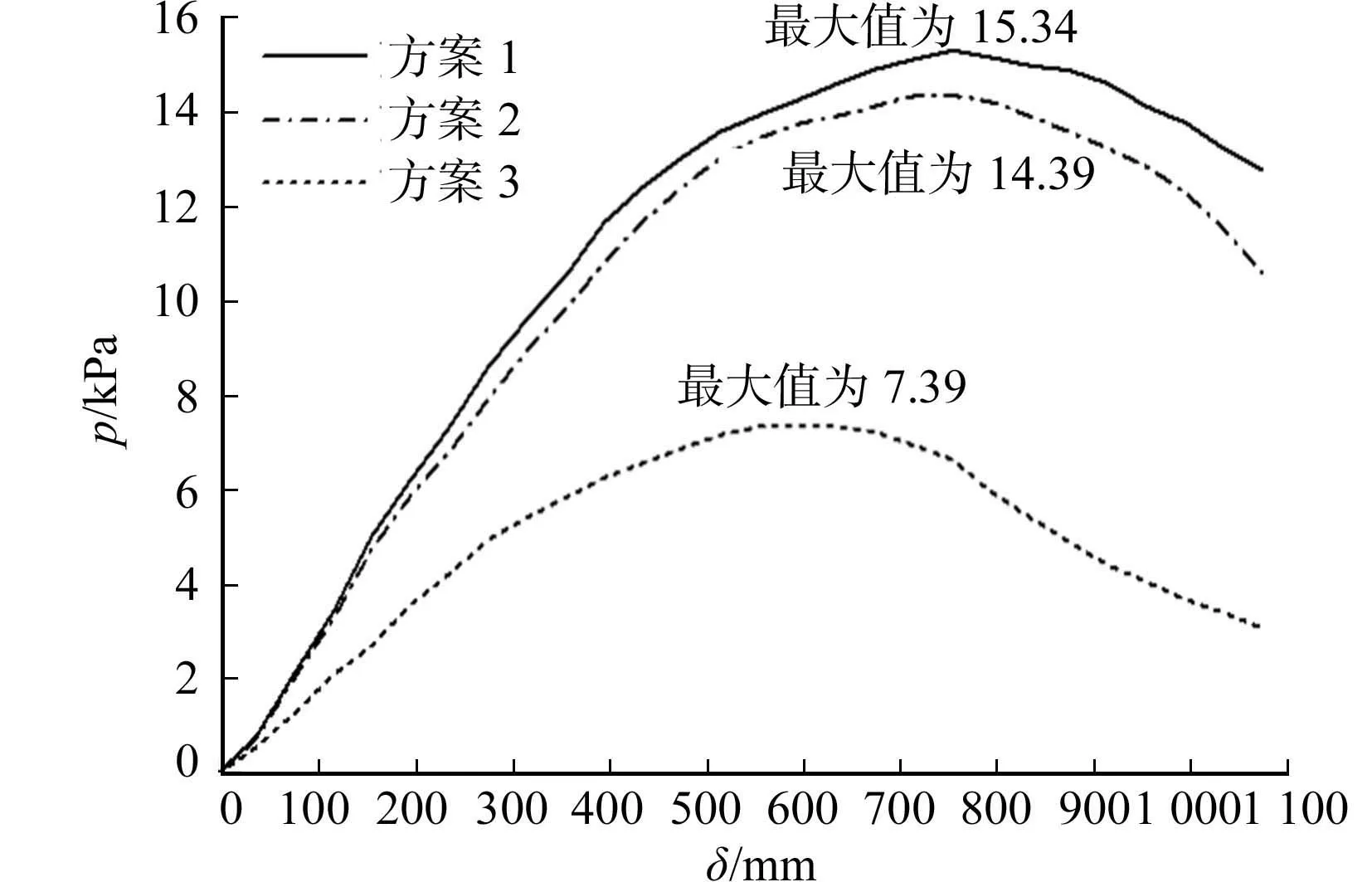
图6 最大位移节点的p-δ曲线图Fig.6 p-δ curves of node with maximum displacement

对网壳结构的优化可以有效减少结构耗钢量，节约成本，但优化后的网壳结构必须满足整体稳定承载力要求.单层球壳的整体稳定性计算依照JGJ 7-2010《空间网格结构技术规程》[14]的相关要求进行.应用ANSYS对原设计方案(方案1)和2种优化方案(方案2，3)进行几何非线性全过程整体稳定性分析.荷载按文献[14]规定取值，满跨均布.初始几何缺陷按结构一阶屈曲模态分布，初始缺陷最大值按文献[14]规定取值，为网壳跨度的1/300(即236 mm).3个方案最大位移节点的荷载(p)-位移(δ)全过程曲线，即整体分析结果如图6所示.

不同的单层球壳设计方案1，方案2和方案3，经ANSYS几何非线性全过程整体稳定性分析，求得的球壳稳定极限承载力分别为15.34，14.39和7.39 kPa.根据文献[14],除以安全系数4.2，即可得到方案1，方案2和方案3的稳定容许承载力标准值puk分别为3.65，3.43和1.76 kPa，均大于球壳的荷载标准值1.70 kPa，满足要求.结果表明：原设计方案1和优化方案2，3的整体稳定性均满足规范要求.

从计算结果可知：优化方案2不改变结构布置形式，结构更轻巧，有较富余的稳定承载能力，其极限稳定承载力相对于原设计仅降低6.2%；不设置内部支承柱的球壳(方案3)相比原方案，在略微降低用钢量的情况下，还可以获得更完整的大空间，但其极限稳定承载力相对于原设计降低较多，已接近设计限值.另外，方案3的最大挠度也接近于设计限值.对比方案2和方案3可知：大跨单层球壳内部设置支柱可调节网壳杆件的内力分布，增加结构的刚度和整体稳定承载力，虽然增加了支柱部分的用钢量，却能有效削减网壳杆件的截面尺寸，综合降低结构总体用钢量.由此可见，对单层球壳进行优化分析是必要的，通过优化方案比较分析，可使设计方案更经济合理.

4 结论

通过对上述内设树枝支承柱大跨球壳结构实例的优化计算和分析，可以得到以下4点结论.

1) 对于复杂形式的大跨单层球壳，进行优化分析和方案比较是必要的，可使结构设计方案节省钢材，更经济合理.

2) 对于周边支承的大跨单层球壳，在强度、杆件稳定、整体稳定和刚度约束条件中，对优化结果起控制作用的是刚度约束条件.应在网壳优化分析中重点考虑刚度约束条件，同时，不可忽视杆件稳定和结构整体稳定约束条件.

3) 除非必需，不设置内部支承柱的球壳可获得完整大空间，通过优化分析可做到不增加网壳结构总用钢量，使设计方案更经济合理.

4) 对于单层球壳内部不需要用到全开阔大空间时，可在网壳内部设置支承柱，并通过优化分析使构件截面合理分布，减轻结构自重，使设计方案经济合理.

[1] 段雷琳,高轩能,江媛.内爆炸下球面钢网壳结构的冲击波超压计算分析[J].华侨大学学报(自然科学版),2013,34(5):557-562.

[2] 王哲,陈志华,王小盾，等.宝坻体育馆扁平椭球壳弦支穹顶设计分析[J].空间结构,2015,21(1):47-53.

[3] 张年文,董石麟,黄业飞，等.考虑几何非线性影响的单层网壳优化设计[J].空间结构,2003,9(1):31-34.

[4] 尚凌云,鹿晓阳.基于离散变量的网壳结构截面优化设计[J].工业建筑,2004,34(9):74-77.

[5] 王法武,唐敢.考虑整体稳定的单层网壳截面优化设计[J].空间结构,2006,12(3):31-34

[6] 徐菁,杨松森,刁延松.单层球面网壳的优化设计[J].空间结构,2006,12(3):35-37.

[7] 刘宗发,李正良,晏致涛.单层球面网壳的优化分析[J].重庆建筑大学学报,2005,27(1):67-70.

[8] 刘宗发,晏致涛,王彦生，等.单层球面网壳选型优化设计[J].重庆建筑大学学报,2007,29(4):83-86.

[9] 陈世英,郭玉霞,鹿晓阳.单层球面网壳结构选型优化设计[J].建筑钢结构进展,2010,10(4):46-50.

[10] 陈世英,鹿晓阳,朱海燕.杆件分组和网格密度对网壳截面优化结果的影响[J].力学与实践,2011,33(2):71-74.

[11] 陈世英,鹿晓阳,王洪利，等.截面优化对网壳结构应力、位移和整体稳定性影响分析[J].空间结构,2014,20(1):45-52.

[12] 陈明明,孟文清,李万庆.基于APDL的大跨度圆柱面网壳结构优化设计[J].钢结构,2013,28(7):39-42.

[13] 郭惠勇,曾虹,李正良.离散变量结构优化设计的理论与方法[J].重庆科技学院学报(自然科学版),2010,12(4):97-100.

[14] 中国建筑科学研究院.空间网格结构技术规程: JGJ 7-2010[S].北京:中国建筑工业出版社,2010:19-20.

(责任编辑： 黄晓楠 英文审校： 方德平)

Optimization Analysis of Single-Layer Spherical Reticulated Shell With Internal Tree Columns

GAO Jian， GAO Xuanneng

(College of Civil Engineering, Huaqiao University, Xiamen 361021, China)

Using genetic algorithm and imitative full-stress method, taking total mass of the structure as objective function and the cross-sectional area of the elements as discrete variable, the optimization analysis of a single-layer spherical reticulated shell with internal tree columns was carried out. Through the comparative analysis of the optimal solutions under constraint conditions such as strength of member, stability of member and stiffness of structure, as well as the geometrically nonlinear whole process overall stability analysis for the optimized spherical shell, the final design scheme was more economical and reasonable. The results indicate that the stiffness condition plays a controlling role on the optimization of spherical shell, stability of member and overall stability of structure can not be ignored. In order to make the design more economical and reasonable for the single-layer spherical reticulated shell with internal tree columns, optimal analysis and scheme comparison are necessary.

single-layer spherical reticulated shell; genetic algorithm; tree-column; optimization analysis

10.11830/ISSN.1000-5013.201606009

2016-02-25

高轩能(1962-)，男，教授，博士，主要从事钢结构及工程结构灾害控制的研究.E-mail:gaoxn117@sina.com.

国家自然科学基金资助项目(51278208); 福建省科技计划重大项目(2012Y4010)

TU 393.3

A

1000-5013(2016)06-0702-06