抛体运动与圆周运动命题规律探究

山东省枣庄二中　朱怀东

抛体运动与圆周运动命题规律探究

山东省枣庄二中朱怀东

一、运动的合成与分解

该热点在高考中主要以选择题的形式进行考查，命题角度有以下几点：（1）根据分运动性质判断合运动性质。（2）根据合运动性质判断分运动性质。（3）考查运动中的临界极值问题。

例1（2014年四川卷）有一条两岸平直、河水均匀流动、流速恒为v的大河。小明驾着小船渡河，去程时船头指向始终与河岸垂直，回程时行驶路线与河岸垂直。去程与回程所用时间的比值为k，船在静水中的速度大小相同，则小船在静水中的速度大小为（）。

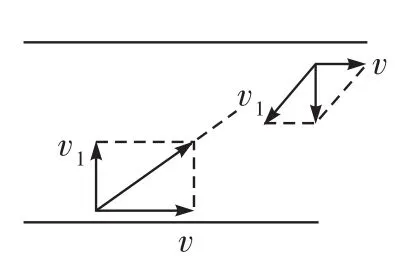
图1

解析去程时船头垂直河岸如图1所示，设河宽为d，由合运动与分运动具有等时性，则去程时间；回程时行驶路线垂直河岸，故回程时间。由题意有，则，得，选项B正确。

例2如图2，在高于河面20 m的岸上有人用长绳拴住一条小船，开始时绳与水面的夹角为30°。人以恒定的速率v=3 m/s拉绳，使小船靠岸，那么（）。

A.5 s时绳与水面的夹角为60°

B.5 s内小船前进了15 m

C.5 s时小船的速率为4 m/s

D.5 s时小船距离岸边15 m

图2

总结提升运动合成与分解的一般思路

（1）明确合运动或分运动的运动性质。

（2）明确是在哪两个方向上的合成或分解。

（3）找出各个方向上已知的物理量（速度、位移、加速度）。

（4）运用力与速度的关系或矢量运算法则进行分析求解。

二、平抛运动规律及应用

命题规律平抛运动的规律是每年高考的重点，有时以选择题的形式出现，有时出现于力学综合题中，有时还以带电粒子在电场中的运动为背景考查类平抛运动的处理方法。

例3（2014年全国卷）取水平地面为重力势能零点。一物块从某一高度水平抛出，在抛出点其动能与重力势能恰好相等。不计空气阻力，该物块落地时的速度方向与水平方向的夹角为（）。

解析设物块在抛出点的速度为v0，落地时速度为v，抛出时重力势能为Ep，由题意知；由机械能守恒定律，得，解得，设落地时速度方向与水平方向的夹角为θ，则，解得，B正确。答案选B。

例4如图3所示，边长为L的正方形ABCD中有竖直向上的匀强电场，一个不计重力的带电粒子，质量为m，电荷量为q，以初速度v0从A点沿AD方向射入，正好从CD的中点射出，而且射出时速度方向与CD成θ=30°的夹角。

图3

（1）该带电粒子带什么电？

（2）该电场的电场强度E为多少？

解析（1）做曲线运动的物体受的合力总是指向曲线凹的一侧，故带电粒子受到的电场力的方向为竖直向下，与电场强度的方向相反，所以粒子应带负电。

（2）带电粒子在电场中做类平抛运动，

则在水平方向上：L=v0t，

在竖直方向上：vy=at，

由牛顿第二定律得：Eq=ma，

总结提升（1）“化曲为直”是处理平抛（类平抛）运动的基本思路和方法。

（2）平抛运动与斜面的结合有下列两种情形：

方法　斜面　内容v0 ___v0分解速度垂直打到斜面　θ vyv θ水平速度vx=v0，竖直速度vy=gt，合速度v=　v2x+v2y■图4 v0 y分解位移___θ水平位移x=v0t，竖直位移y=1 x 2gt2，θ合位移x合=　x2+y2■图5

三、圆周运动问题的分析

命题规律该知识为每年高考的重点和热点，题型既有选择题，也有计算题。近几年的高考命题规律主要有以下几点：

（1）圆周运动与平衡知识的综合题。

（2）考查圆周运动的临界和极值问题。

（3）与平抛运动、功能关系相结合的力学综合题。

例5（2014年全国卷）如图6，一质量为M的光滑大圆环，用一细轻杆固定在竖直平面内；套在大环上质量为m的小环（可视为质点），从大环的最高处由静止滑下。重力加速度大小为g，当小环滑到大环的最低点时，大环对轻杆拉力的大小为（）。

A.Mg-5mgB.Mg+mgC.Mg+5mgD.Mg+10mg

图6

解析方法一：以小环为研究对象，设大环半径为R，根据机械能守恒定律，得，在大环最低点有，得FN= 5mg，此时再以大环为研究对象，受力分析如图7，由牛顿第三定律知，小环对大环的压力为FN′=FN，方向竖直向下，故F=Mg+5mg。由牛顿第三定律知C正确。

图7

图8

方法二：设小环滑到大环最低点时速度为v，加速度为a，根据机械能守恒定律，且，所以a=4g，以整体为研究对象，受力情况如图所示。F-Mg-mg=ma+M·0，所以F=Mg+ 5mg，C正确。

例6（2014年安徽卷）如图9所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω转动，盘面上离转轴距离2.5 m处有一小物体与圆盘始终保持相对静止。物体与盘面间的动摩擦因数为（设最大静摩擦力等于滑动摩擦力），盘面与水平面的夹角为30°，g取10m/s2。则ω的最大值是（）。

图9

解析当物体转到圆盘的最低点恰好不滑动时，转盘的角速度最大，其受力如图10所示（其中O为对称轴位置）

图10

由沿斜面的合力提供向心力，有μmgcos30°-mgsin30°=mω2R，

总结提升解决圆周运动力学问题要注意以下几点

（1）要进行受力分析，明确向心力的来源，确定圆心以及半径。

（3）对于竖直面内的圆周运动，要注意“杆模型”和“绳模型”的临界条件。

四、平抛与圆周运动的组合问题

曲线运动的综合题往往涉及圆周运动、平抛运动等多个运动过程，考查运动的合成与分解、牛顿第二定律和功能关系等知识，常以计算题的形式呈现。

图11

（1）求物块到达B点时对圆形轨道的压力大小。

（2）求物块做平抛运动的时间。

（3）若下滑过程中某时刻物块和木板达到共同速度，则这个速度为多大？

由牛顿第三定律可知物块对轨道的压力为3 N。

对物块：v′=v+a1t，a1=g（sinθ-μcosθ）=2.5 m/s2，

对木板：v′=a2t，a2=g（sinθ+μcosθ）=7.5 m/s2，

总结提升解决平抛与圆周运动的组合问题时极易因以下几点出错：①不能熟练掌握平抛运动和圆周运动的规律；②找不到衔接两种运动过程的关键物理量；③对竖直面内圆周运动的几种模型不能熟练掌握，找不出向心力。

应从以下几点进行防范：①熟练掌握各个运动过程的运动规律；②注意运动速度如何变化，机械能是否守恒；③要善于抓住转折点或临界点的速度进行突破；④明确各子过程或全过程有关物理量的变化规律。