基于激励机制优化模型下现行“打车软件”的改进分析

王锐杰,杨鹏辉,贾斯钰,黄丽华

(安徽财经大学 a. 金融学院; b. 统计与应用数学学院， 安徽 蚌埠 233030)



基于激励机制优化模型下现行“打车软件”的改进分析

王锐杰a,杨鹏辉b,贾斯钰b,黄丽华b

(安徽财经大学 a. 金融学院; b. 统计与应用数学学院， 安徽 蚌埠 233030)

针对打车软件对缓解打车难的绩效分析问题,建立了一个基于空驶量的司乘推荐模型,并对现有打车软件进行了评价分析.进一步根据评价分析结果,利用激励机制约束模型和借助MATLAB软件创建出具有自动搜寻最优补贴方案功能的打车软件服务平台.最后以北京市为例,对改进后的打车服务平台进行实证分析,验证了平台的合理性.

打车软件改进；司乘推荐模型；激励机制约束； MATLAB

近年来,随着“互联网+”概念的推出,利用信息技术和互联网平台来发展各行各业正冲击着我国的传统行业.出租车公司这一传统行业现在也正面临着这一挑战.在这样的大环境下,出租车市场涌现出了以滴滴打车与快的打车两家软件公司为代表的多款打车软件,深受用户追捧.打车软件借助发达的信息网络技术及用户大数据的优势,并通过对司机和乘客双方进行不同程度的补贴,极大提高了出行者的打车成功率,实现了乘客与出租车司机的共赢,进而在我国各大城市得以快速发展.但是由于其发展过快,打车软件自身存在着管理体制和盈利模式上的缺陷,致使出租车市场出现规模扩大过快、道路交通资源浪费及配置不合理等问题.同时对于打车软件公司推出的补贴方案是否真的可以缓解“打车难”问题仍值得考究.因此综上所述,通过分析现有打车软件的存在的不足并对其进行改进对出租车资源的合理配置及寻找缓解“打车难”的最优方案都具有较深远的意义.

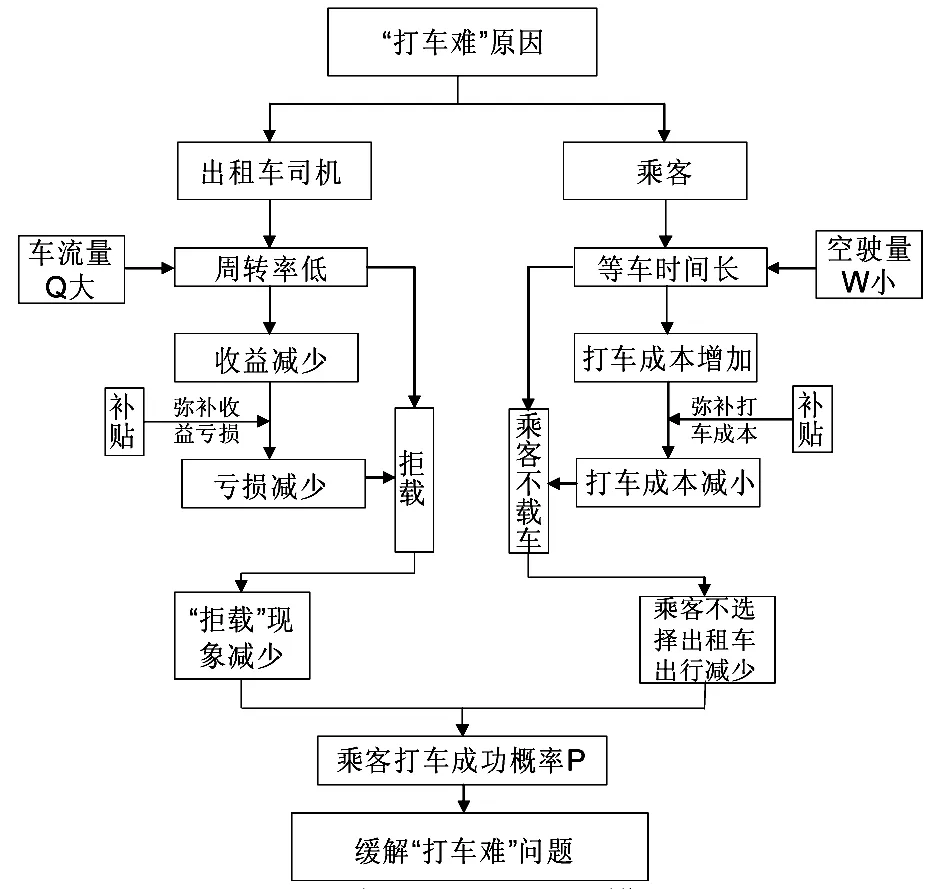
图1 基于空驶量的司乘推荐模型思路图

1 现有“打车软件”绩效评价分析

1.1 研究思路

近年来我国出租车市场涌现出越来越多的“打车软件”,究其是否真的可以缓解城市“打车难”问题有待商榷.针对这一问题的解决办法,主要得找出影响“打车难”的根本原因.经查阅相关文献得知,目前对这一问题研究大多数所采用模型的是司乘推荐模型[1],但是该模型其仅仅考虑了一些简单客观影响因素,并没有将主要影响因素考虑其模型中,导致分析效果不佳.因此本文在该模型基础之上进行了优化设计,并从乘客和司机双方出发分析将影响“打车难”的主要因素量化,从而建立了一个基于空驶量的衡量“打车难”的司乘推荐模型,具体建模思路见图1.

1.2 模型建立

1.2.1“周转率—车流量”联合关系函数

从出租车司机角度出发,发现之所以出现“拒载”、“挑客”现象,主要是由于出租车司机“周转率”较低引起的.为了较好地反映观测“周转率”这一指标,本文建立了车流量与周转率间的联合函数.

其中:P1为出租车起步平均价；ΔP为超出规定里程的费用；u为出租车司机的补贴费用;v为出租车司机的补贴费用；C为周转率；Q为车流量；S为司机总收益；Gn为出租车行驶公里折旧系数.

1.2.2“乘客等候时间—空驶量”联合关系函数

同时,从乘客角度出发,经分析发现,乘客等候时间的长短是影响乘客是否打车的主要因素.一般情况下乘客等候时间越长,出行人们选择出租车的概率越低[2],而在一定程度上,其与空驶量W存在较大关系,一般空驶量越大,乘客等候时间越短；反之越长.因此在既定条件下可以建立如下关系式：

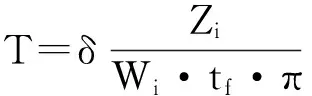
其中:T为乘客等候时间；W为空驶量；Zi为第交通区车辆达到率(辆/h)；tf为出租车的平均搜索乘客时间(min)；p为乘客乘车补贴费.

1.2.3“打车概率”函数

为了定量地分析打车难易程度,本文以“打车概率”作为绩效评价关键,利用可以量化的“打车概率”来衡量打车难易程度.经发现,打车概率在一定程度上与车流量和空驶量存在关系.因此利用上述所建关系,最终可得到打车概率函数表达式为

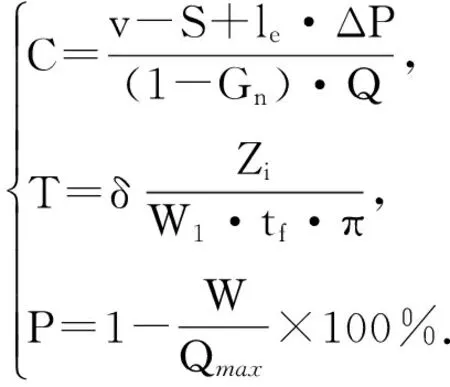
1.3绩效分析

经调查研究发现,打车软件公司在缓解打车难这一问题时,主要采用了向乘客和司机双方进行补贴的方法.为此本文主要以快的打车和滴滴打车两家主要打车软件公司为研究对象,结合上文所建模型对其是否能够缓解打车难进行客观分析.

以快的打车为例,其补贴是以出租车每次接单数为基础进行补贴,即每接一次单成功后给司机和乘客都进行补贴.通过统计补贴金额得知,快的打车乘客补贴均值为每单9.8元,给司机补贴均值为8.7元.则根据δ=T·(1-Gn)·m司机补贴单价;v=T·(1-Gn)·m乘客补贴单价.其中,m司机补贴单价为向司机平均每单补贴金额,m乘客补贴单价为向乘客平均每单补贴金额.

按上述分析可得，δ1=T·(1-Gn)·m司机补贴单价=164元，v1=T·(1-Gn)·m乘客补贴单价196元,将其代入打车成功概率模型得：

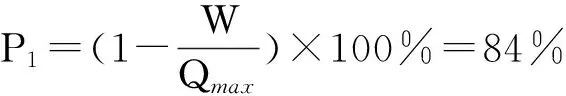
再以滴滴打车为例,其通过统计变化的补贴金额,滴滴打车乘客补贴均值为每单12.5元,给司机补贴均值为9.2元.因此可得其补贴方案实施之后的打车概率为：

对比分析传统出租车公司发现,其只针对出租车司机进行补贴.例如,每车每年补贴运营费17733.6元；每车每天补贴运营费49.26元；每车每年补贴燃油费用为9326元；每车每天补贴燃油费用25.5元.利用上述数据我们可得传统方案下总补贴费d=d0+d1=49.26+25.5=74.76元,最终得到其打车概率P为55%.经上述分析所得数据可知,我们利用EXCEL软件各个补贴方案下的打车成功率画出打车成功率变化曲线图,如图2：

图2 打车成功率折线图

从图2中可见,打车软件公司推出的补贴方案比传统公司的补贴方案提高的打车率要高出39%～42%.说明对乘客进行补贴,能提高乘客的耐心,使得乘客愿意花更多的时间去等车；另一方面打车软件公司变更了对司机的补贴方案,调动了司机接单的积极性,只要接单就有较高的利益,省去了因交通拥堵而出现的“拒接”现象,提高了出租车资源利用率.而且其利用了现如今日臻完善的互联网技术平台,极大提高了信息利用率,从而大大缓解了打车难问题.但是从一定程度上讲,上述两家公司补贴方案并没较好解决高峰路段打车难问题,从而说明打车软件还存在改进空间.

2 对现有“打车软件”改进的实证研究

2.1 研究思路

为了弥补目前市场上出现的打车软件具有的缺陷,设计出更好的打车软件服务平台[3].本文将首先利用委托-代理中的激励机制模型,并借助Matlab7创建一个具有自动寻优补贴方案的智能打车软件服务平台.然后利用上述新的打车服务平台,设计出优化处理后的“补贴方案”.最后,选取北京市五个典型地区进行研究,依据新的打车服务平台得出各地区的补贴方案,并通过对比分析实施补贴方案前后打车成功率的变化验证其打车服务平台是否具有合理性.

2.2 打车软件服务平台的优化设计

2.2.1基于第三方软件平台公司激励机制的优化匹配模型构建

在研究过程中,假定第三方打车软件公司[4]为委托人,其风险是中性的,出租车司机为代理人,风险可规避.在给定的合同下,可以得到其期望收入如下：

En(m-S(m))=E(g+b(m-m0)))=-g+bm+aw(1-b),

其中:S(m)=g+b(m-m0);m为出租车司机的补贴金额;a是公司累计补贴能力系数;b为第三方打车软件公司的激励强度;g是第三方打车软件公司给予出租车司机基础补贴.

同时,假设司机因第三方软件补贴程度增加其运营成本,而出租车司机因接受第三方软件公司的补贴而使运营成本降低,故而司机的实际收入为：

q=S(m)-d(w)=g+b(m-m0)-cw2/3.

令Sb为司机的保留收入,则如果司机的确定性等价收入小于q时,司机将可以不接受公司给与的补贴,因此,司机的参与约束IR为：

其中es2b2/2为司机的风险成本.

最后在最优情况下,将参与约束通过固定项γ代入目标函数,并将结果代入司机的参与约束IR得：

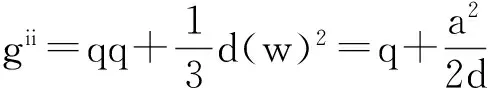
其中gii为可观测条件下的帕累托最优解.最优解是指在代理人不承担任何风险的情况下,第三方打车软件补贴给司机的金额正好等于司机的保留收入与运营成本之和.这时该软件对出租车司机的累计补贴是满足司机和乘客利益最大化的解,它是由第三方软件根据乘客与司机所处的地理信息,系统自动累加加权,最终使司机与乘客满足利益最大化.

2.2.2新补贴方案的设计

在设计新方案时,通过建立第三方打车软件激励机制的优化匹配模型[5],使其系统通过分析乘客与出租车司机的所处地理位置,根据乘客与司机的距离及乘客所处交通路段的情况自动模拟出累计加权补贴,最终使得乘客成功打到车,提高其打车成功率.根据Matlab7软件运行结果得到新补贴方案如下表：

表1 激励机制模型下不同情况下的补贴方案表

附：新打车软件实施积分制运营,即每当司机接一个“差单”可得多少积分,而该积分达到一定程度可帮助司机抢单,即在两出租车与乘客距离一样的情况下,积分多的司机抢单成功率大.

2.3 实证结果分析

为了验证改进后的打车软件服务平台其效果如何,本文选取了北京市五个典型地区作为研究地区,并借助“苍穹”智能出行平台[6]收集统计各个地区相关补贴方案下的相关数据,如下表：

表2 各地区相关补贴下的数据表

将上述五个不同地区具体补贴方案代入打车概率模型,可以得到补贴之后的打车成功率,并与之前补贴方案下的打车概率进行对比,如表3：

表3 北京市A～E不同地区补贴前后打车概率对比表

从上表可得,改进后的补贴方案效果与软件公司补贴方案效果相对比,打车成功率在一定程度上都有了提高.朝阳路成功率提高了2.8%,陶然亭提高了3.4%,白石桥提高了0.94%,学院路提高了9.7%,建国门提高了4.1%.增加高峰路段每次乘客叫单所增加的补贴金额,在一定程度上缓解了早晚高峰期打车难的问题,降低了出租车司机“拒接”的概率,使得出租车资源得到了更加有效地利用,弥补了之前打车软件的不足,也说明了改进后的方案是合理的.

3 关于影响设计平台运行结果的重要指标修正

3.1 研究思路

由于本文中两个重要模型都用到了“车流量”这一重要指标,因此该指标数据的准确性直接决定着模型设计可靠性.而上述模型中在收集该指标数据时,采用了“苍穹”智能出行平台提供的数据,其来源的可靠性以及可用性都值得作进一步验证及修正.通过数据分析,该指标数据属于时间序列数据,为此本文决定建立“车流量”的时间序列预测模型[7],借助EVIEWS软件对其预测数据进行合理性修正,尽可能使其与实际数据相吻合.

3.2 研究方法—时间序列预测模型

对上述论文中“车流量”运用EVIEWS软件做时序图(图3). 由图中容易看出,该组数据不平稳.为了满足预测模型的条件,对数据进行对数LOG处理,设得到平稳序列y1,对y1的平稳性进行单位根检验见图4,由检验可知：该序列单位根检验值的绝对值大于给出的显著性水平1%-10%的ADF临界值,落在拒绝域内,拒绝原假设,故该序列为平稳序列.

图3 出租车的需求量时序图

图4 LOG变换后的平稳性检验图

接着对y1做自相关、偏自相关分析,并分别建立序列AR(1)、MA(1)、ARMA(1,1),并比较三种序列的AIC和SC值,如表4：

表4 AR(1)、MA(1)、ARMA(1,1)模型的AIC和SC的比较

据表4可得,由于AIC：2.54>-0.59>-0.92,SC：2.63>-0.51>-0.79,易知ARMA(1,1)模型较为合理,能更好的对数据进行拟合.同时可以得到模拟ARMA(1,1)模型表达式：

ARMA(1,1)∶xt-5.10=0.74(xt-1-5.10)+et+1.00et-1.

为保证模型的完整性,对序列ARMA(1,1)进行残差检验后发现[8],P检验值大于临界值0.05,落在不拒绝域内,所以不能拒绝原假设,即该序列为白噪声序列,也就说明可用上述序列表达式对“车流量”进行预测.

4 结语

本文在分析“打车软件”缓解打车难绩效时,从乘客和司机两个影响“打车难”的主要因素出发,并结合实际所收集数据的能力,寻找不同因素间的相关联系,巧妙地用简单易搜集的指标代替较难搜集的指标,并最终建立了基于空驶辆的司乘推荐模型,为目前定量分析“打车软件”绩效提供了参考.另外,文章的重点研究方向是对现有打车软件的改进.通过对现有打车软件绩效评价分析,发现其虽然相比传统出租车公司较大提高了市民出行打车成功率,但是并没有较好解决高峰路段打车难问题.为此,本文结合激励机制约束模型,创建出了一种具有自动搜寻最优补贴方案功能的打车软件服务平台,也是本文的主要创新之处,可为现有打车平台改进提供借鉴.在理论基础上验证后发现,该服务平台较好地解决了高峰路段打车难问题,弥补了现有打车软件的不足.

[1]刘仰东,田野,袁博,等.一种基于车流量的司乘推荐模型[J].科研信息化技术与应用,2015,6(3):66-73.

[2]林玉川.移动打车软件用户行为研究[D].厦门:厦门大学,2014.

[3]王一帆. 基于打车软件的出租车服务模式优化研究[D].上海:上海交通大学,2014.

[4]陆佳敏.论企业绩效激励机制的构建[J].财经界(学术版),2010,(9):76-77.

[5]秦永召. P2P网络的激励机制设计与实现[D].太原:太原科技大学,2013.

[6]苍穹智能出行平台[DB/OL].(2015-05-10)[2016-3-1].http://v.kuaidadi.com/ download/2015/20150509

[7]张浒.时间序列短期预测模型研究与应用[D].武汉:华中科技大学,2013.

[8]杨桂元,朱家明.数学建模竞赛优秀论文评析[M].合肥:中国科技大学出版社,2013.

(编校：曾福庚)

Improvement of Taxi Software Based on the Incentive Mechanism Optimization Model

WANG Rui-jiea,YANG Peng-huib,JIA Si-yub,HUANG Li-huab

(a. School of Finance, b.School of Statistics and Appl. Math, Anhui University of Finance and Economics, Bengbu Anhui 233030, China )

Aiming to analyzing the performance of Taxi Software which seeks to ease the taxi difficulty, a taxi passenger-driver recommendation model was established based on the amount of empty ride. Meanwhile, the existing Taxi Software was evaluated. Furthermore, according to the results of evaluation and by applying the optimizing model based on the incentive mechanism and with the help of MATLAB software, the Taxi Software service platform was created with the function of automatically searching the Optimal Subsidy Scheme. Finally, by taking urban Beijing as an example, the improved taxi service platform is proved reasonable after empirical analysis.

Taxi Software improvement; tax passenger-drive recommendation model; incentive mechanism; MATLAB

2016-03-20

国家大学生创新创业训练计划项目(201510378050)；国家自然科学基金资助项目(11301001)

杨鹏辉(1981-),女,安徽省淮南市人,安徽财经大学统计与数学应用学院讲师,硕士,主要研究方向为应用数学与数学建模.

F572.88

A

1008-6722(2016) 05-0114-06

10.13307/j.issn.1008-6722.2016.05.22