基于初始值优化的灰色马尔科夫链预测模型研究

李志亮，罗 芳

(宁德师范学院 计算机系，福建 宁德 352100)



基于初始值优化的灰色马尔科夫链预测模型研究

李志亮，罗 芳

(宁德师范学院 计算机系，福建 宁德 352100)

在传统灰色GM(1，1)预测模型的基础上，首先对预测模型的初始值进行优化，然后采用马尔科夫链对优化后的模型进一步改进，建立了一种基于初始值优化的灰色马尔科夫预测模型，优化后的模型可以有效提升预测的准确性和稳定性.最后通过对宁德市旅游入境总人数的实例分析，验证了新模型的有效性，拓展了灰色预测模型的应用范围，为宁德市旅游事业的发展提供了一种新方法和新思路.

初始值优化;马氏灰色预测模型;实例分析

0 引言

近年来，随着旅游行业的快速发展，宁德市旅游产业规模越来越大，并且带来的经济效益日益扩大，旅游业已经成为宁德市社会发展和经济发展的重要推动力量.旅游人数是衡量旅游业发展的重要指标，与当地经济发展和人民消费密切相关，而旅游人数的预测对于促进旅游业的发展有着重要的影响.目前旅游人数预测主要的方法包括时间序列法、神经网络预测模型和灰色预测模型等[1]，这些预测模型中，灰色理论[2]中的GM(1，1)灰色预测模型具有数据样本小、计算简单、预测结果与实际结果较为拟合等特点，已经被众多学者研究和应用[3]，并且很多学者已经对GM(1，1)灰色预测模型进行了优化和改进[4-5].王晓霞等运用GM(1，1)灰色预测模型建立了旅游人数预测模型，并应用到牡丹江市的旅游人数预测中，得到了未来旅游人数的变化规律[6].王璐等对GM(1，1)模型进行优化，并实例验证了优化后模型在预测结果上的有效性[7].优化后的灰色预测模型已经越来越多的应用到旅游领域中，并起到了较好的效果[8-9].

虽然GM(1，1)模型具有上述优点，但是其在预测波动性较强的数据序列时预测效果较差，并且在初值的选取方面还有待进一步的优化[10]，而马尔科夫链对于数据随机波动较大的预测具有较好的预测精度和稳定性[11]，因此采用马尔科夫链对GM(1，1)灰色预测模型优化有着较好的理论基础和科学依据.

结合上述学者的研究以及旅游历史数据随机波动较大的特点，首先在传统灰色GM(1，1)预测模型的基础上，拓展预测数据的范围，优化GM(1，1)模型预测过程中的初始值.然后通过马尔科夫链对优化模型进行进一步的修正，进而提高预测模型的预测精度和稳定性.最后以宁德市旅游入境总人数预测为例，对比传统灰色预测模型的预测结果、改进预测模型的预测结果和实际旅游相关数据结果，验证优化预测模型的准确性和稳定性.

1 灰色GM(1，1)预测模型中初始值的优化

传统的GM(1，1)预测模型，在一步累加得到的序列具有较强的灰指数率，参数a,b的选取对预测精度有着重要的影响，而原始数据和模型的初始值又直接影响这参数a,b的值，因此初始值的优化对GM(1，1)预测模型的预测精度有着重要的影响.传统的初始值是采用公式(1)进行计算初始值的，具体如下：

X(1)(i)=0.5×(X(0)(i)+X(0)(i-1)).

(1)

上述初始值的选取没有对后续信息的利用，因此会对预测结果的精度产生不良影响.本文在传统初始值计算的基础上，通过对传统初始值计算的优化，来提高预测精度.本文中选取预测值残差最小的X(1)的分量X(1)(i)最为灰色预测模型的初始条件，这样充分利用了后续的新信息，可以较好的提高预测精度，初始值的选取公式如下：

X(1)=min(X(1)(i))，

(2)

其中i=1,2,…n.

则初始值优化后灰色预测模型的时间响应表达式为：

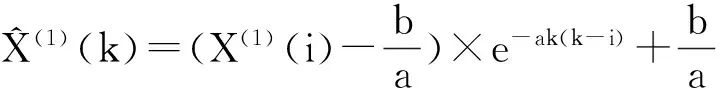
(3)

恢复原始序列，得到预测值：

(4)

2 马尔科夫链修正后的模型

在初始值优化的基础上，结合马尔科夫链理论，建立初始值优化的灰色马尔科夫链预测模型，进一步提高预测的稳定性和准确性.具体步骤如下：

1)计算残差

由公式(5)计算残差序列，用E(0)(k)表示:

(5)

其中k=1,2,…n.

2)划分残差状态

根据公式预测模型中的残差大小，划分为m个状态，每个状态用Si表示，其中：Si∈[Li,Hi].Li和Hi表示第i个状态的上下边界：

(6)

其中k=1,2,…n;i=1,2,…m.

3)构造状态转移概率矩阵

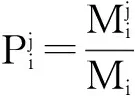
(7)

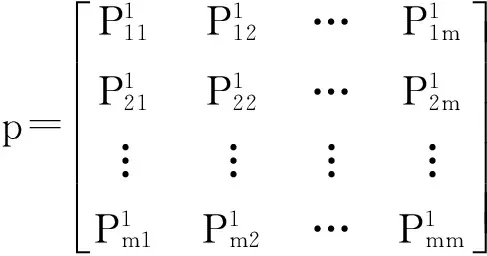
(8)

4)得到预测值 根据状态转移概率矩阵，得到预测值：

(9)

其中：ui(t)表示灰色残差序列中从上一个状态变换为下一个状态的概率，参数t为转移的时间，vi表示区间的中点.

3 实例分析

采用宁德市近7年的旅游收入数据，数据来自宁德市国民经济和社会发展统计公报，以宁德市旅游入境总人数数据为例，利用前6年宁德市旅游入境总人数的历史数据进行建模，预测宁德市旅游入境总人数，原始的历史数据见表1.

表1 2010-2015年宁德市旅游入境总人数

注：表中总人数和后续表中的预测值与实际值的单位均为万人.

根据表1中的实际数据，采用传统的GM(1，1)预测模型和初始值优化后的灰色预测模型，对2010年后的宁德旅游入境总人数进行预测，把预测结果、残差分析和实际总人数进行对比.具体结果如表2.

表2 两种预测模型的预测值、残差和实际值

由表2可以看出，通过初始值优化后预测结果比传统的GM(1，1)预测模型的预测结果更为准确，其残差更小，波动幅度值更低.两种预测模型对2015年宁德市入境总人数预测的结果分别是1877.91万人和1857.6501万人，而2015年宁德市旅游入境总人数为1837.4万人，可见预测结果随着数据的增多，其波动值基本是降低趋势，但是在波动范围较大的变化时，比如2012年旅游人数急剧增加的时候，两种预测方法的预测结果都有较大的波动，但比较起来，初始值优化的预测模型较原始GM(1，1)预测模型的预测结果具有更高的准确性和稳定性.

下面通过马尔科夫修正的灰色预测模型，对宁德市旅游总收入进行进一步的预测，过程如下.

1)划分残差状态

根据表2中的残差值，划分残差状态数量为3个，分别表示增长趋势减缓、增长趋势增长和增长趋势较快三个状态，分别用S1、S2和S3，残差采用初始值优化后的残差结果，其区间范围分别为：

S1∈[-36.1794,-25.3187],S2∈[-25.3186,6.5251],S3∈[6.5252,53.0625].

2)构造状态转移矩阵

根据表2中残差修正的数据，结合残差状态划分，将表2中的数据残差划分为3个状态，得到表3.

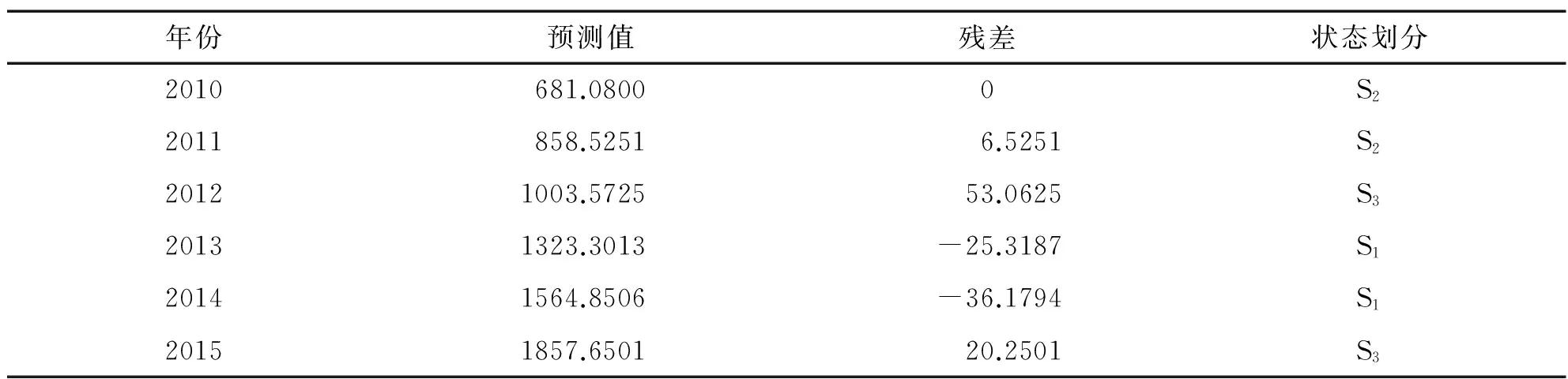
表3 宁德市旅游总收入预测与残差状态划分

通过公式(11)计算状态转移矩阵，结合表3中状态划分，得到宁德市旅游入境总人数的状态转移矩阵P：

3)得到预测值

结合状态转移矩阵，根据公式(13)得到预测值，预测结果见表4.

表4 灰色马尔科夫模型预测结果

由表4可以看出，随着数据量的增多，数据预测呈现更好的稳定性和准确性，在初始值优化基础上的灰色马尔科夫预测模型，可以更精确的预测宁德市旅游入境总人数，特别是在数据波动较大的2012年，其预测结果与初始值优化后的预测模型比较，和真实值的拟合性更好.

把传统的GM(1，1)模型、初始值优化后的预测模型和灰色马尔科夫优化后的预测模型的预测值进行整合，把三种预测模型的预测结果与真实值进行汇总分析，得到表5，表5中数据反映了三种预测模型与真实值的拟合情况.从表5可以看出，基于初始值优化的灰色马尔科夫预测模型具有更好的拟合性，与真实值的残差更小，即预测结果更准确，稳定性更好.

表5 三种预测模型预测结果与实际值

从表5中数据可以得出，对传统GM(1，1)灰色预测模型改进过程中，预测结果的残差是呈降低趋势的，即初始值优化模型的残差小于传统GM(1，1)预测模型的残差，而灰色马尔科夫预测模型的残差比初始值优化的预测模型残差更小，各种预测模型的残差计算结果如表6.

表6 三种预测模型残差结果比较

由表6的残差数据对比可以看出，灰色马尔科夫预测模型除了2011年预测的残差较大外，其余年份预测结果残差都是最小的，这说明随着数据量的增多，其预测结果越来越拟合实际值，而且其在2012年数据波动性较大时的预测结果与实际结果更为拟合，验证了基于初始值优化的灰色马尔科夫预测模型的有效性和准确性.

4 总结

本文从传统灰色预测的GM(1，1)模型的局限性出发，通过初始值优化和马尔科夫链对GM(1，1)模型进行优化，优化的灰色预测模型可以较好的解决传统GM(1，1)预测模型对随机波动数据预测结果不够准确的问题，拓展了传统灰色GM(1，1)预测模型的应用范围，并较好的提高了预测精度和稳定性.最后将优化的灰色预测模型应用到宁德市旅游入境人数的预测中，预测了宁德市旅游入境总人数，并与传统GM(1，1)预测模型和实际值进行对比，通过实例数据对比验证了优化预测模型的有效性和准确性，为旅游业的发展提供决策支持.

未来工作中将进一步优化残差修正，寻求更优残差修正值，进一步提高预测的精度和准确性.同时对其他的灰色预测模型进行研究，包括灰色Verhulst预测模型，深入研究这些模型的特点，拓展灰色预测模型的使用范围，提升灰色预测模型的预测精度.

[1]王哲河,林越,张侨. Dijkstra算法在三亚旅游线路规划中的应用[J].琼州学院学报,2015,22 (5):98-102.

[2]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.

[3]刘思峰.灰色系统理论及其应用[M].7版.北京:科学出版社,2014.

[4]何俊,张玉灵.灰色预测模型的优化及应用[J].数学的实践与认识,2013,43(6)：86-89.

[5]李克昭,李志伟,赵磊杰.马尔科夫理论的优化灰色模型预测建模[J].测绘科学,2016,41(8)：1-5.

[6]王晓霞,祖培福,潘伟.牡丹江旅游人数预测研究的灰色动态数学模型[J].数学的实践与认识,2013,43(16) : 35-39.

[7] 王璐,沙秀艳,薛颖.改进的GM(1,1)灰色预测模型及其应用[J].统计与决策, 2016(10): 74-77.

[8]何俊,张玉灵,刘银萍.基于灰色马尔科夫链的河南省旅游总收入预测[J].河南科学,2016,44(4) :686-690.

[9]曾冬玲,喻科,赵清俊.基于灰色理论和马尔科夫修正的旅游需求预测——以云南省旅游市场为例[J].重庆工商大学学报( 自然科学版) ,2016,33(4) : 58-68.

[10]刘慧敏,樊锁海.基于灰色系统理论的广州市旅游接待人数预测与分析[J].统计与决策,2010(17):64-66.

[11]李沛杰,张兴明,沈建良.灰色-隐马尔科夫下的信任路径筛选及聚合算法[J].小型微型计算机系统,2015,36(5):964-970.

(编校：曾福庚)

A Gray - Markov Chain Prediction Model Based on the Optimization of Initial Value

LI Zhi-liang，LUO Fang

(Department of Computer, Ningde Normal University, Ningde Fujian 352100, China)

On the basis of the traditional grey GM (1, 1) prediction model, the initial value of the forecasting model was optimized, and then Markov chain was used to further improve the optimized model. Based on the initial value optimization, a grey Markov prediction model was established. Consequently the optimized model can effectively improve the accuracy and stability of the prediction. Finally in order to provide a new method and new idea for the development of tourism in Ningde, by analyzing the instance of the total number of Ningde city tourism entry, the validity of the new model is verified, meanwhile the application range of the grey prediction model is expanded.

optimization of initial value; Markov Gray forecasting model; case analysis

2016-09-07

福建省中青年教师教育科研项目(JAT160543)；福建省大学生创新创业训练计划项目(201610398042)；宁德师范学院青年专项(2015Q05)

李志亮(1981-)，男，山东禹城人，宁德师范学院计算机系讲师，研究方向为不确定系统理论.

O211.62；N941.5

A

1008-6722(2016) 05-0055-04

10.13307/j.issn.1008-6722.2016.05.11