对角线元为幂等矩阵的2×2分块方阵的数量幂等性
2016-12-06于明明
于明明,吴 炎
(海南热带海洋学院 数学系, 海南 三亚 572022)
对角线元为幂等矩阵的2×2分块方阵的数量幂等性
于明明,吴 炎
(海南热带海洋学院 数学系, 海南 三亚 572022)
设G是对角线元为幂等矩阵的2×2分块方阵,利用矩阵理论和方法,研究并得到了对角线元为幂等矩阵的2×2分块方阵G的k次数量幂等性,确定了方程Gk=λG有解的充要条件,其中k=2,3.
数量幂等矩阵;分块矩阵;数量幂等性
1 引言与预备知识
2×2分块矩阵的特殊性质(包括矩阵块独立性的结果),对于矩阵的广义逆的研究,以及线性统计估计与等式约束二次规划问题的研究均有重要理论意义和应用价值[1-3],特别是分块矩阵的加权M-P逆在线性统计推断、预报理论、控制系统分析、曲线拟合、数值分析等领域均有很好的实际应用[2].
文献[1-3]主要研究分块矩阵g一逆和加权M-P逆的块独立性,得到两个和三个复矩阵块独立的充分必要条件,并揭示了不同定义下的块独立性定义之间的联系.文献[4]主要对幂等和n阶k次幂等矩阵的一些秩性质进行研究,而文献[5]利用矩阵方法给出了局部环上高次幂等矩阵的伪标准型和3次幂等矩阵的相似标准形及其在广义逆中的应用.文献[6]研究了m次数量幂等矩阵线性组合的可逆条件.文献[7]则从另一方面研究并得到了局部环上3个幂等矩阵线性组合的广义逆之间的关系,以及这些广义逆之间包含关系成立的条件.文献[8]主要研究了在一定条件下,复分块矩阵是幂等矩阵且某些性质成立时,关于复分块矩阵的广义Schur补的性质.文献[9]利用矩阵理论研究了相似变换下的幂零矩阵的{2,3}-逆问题,而文献[10]利用矩阵理论和矩阵计算技巧研究了对角线元为数量幂等矩阵的高阶上三角分块矩阵的数量幂等性,并给出了2×2分块上三角矩阵的{1,3}-逆表示式.
然而,上述文献都没有考虑关于对角线元为数量幂等矩阵的非上、下三角的一般2×2分块矩阵的特殊性质(如幂等性等)的研究,因此其实质性问题仍待需要进一步的探讨.本文利用矩阵理论和矩阵计算方法,特别是幂等矩阵的相似标准形理论,在实数域上研究了对角线元为幂等矩阵的一般2×2分块方阵的低阶数量幂等性质,得到若干个比较整齐的充要条件和结果.
为了使用方便,本文中用R表示实数域,用Rn×n表示R上所有n×n阶矩阵的集合,用En表示n阶单位矩阵,用r(A)表示矩阵A的秩,用N+表示全体正整数集,用A⊕B表示对角矩阵diag{A,B}.
定义1[6]设A∈Rn×n,λ∈R(λ≠0).若存在最小正整数k∈N+,使得Ak=λA,则称A为k次幂等矩阵.
在本文中,不失一般性假设A∈Rn×n,D∈Rs×s,A2=A,D2=D(A≠0,D≠0;n,s∈N+),且不妨设r(A)=r,r(D)=t,则由文献[5]易知,存在P1∈GLn(R)和P2∈GLs(R),使得
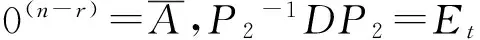
利用上述非零的幂等矩阵A,D和矩阵B∈Rn×s,C∈Rs×n构作如下2×2分块方阵
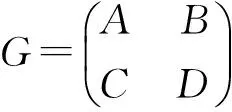
(1)
令P=P1⊕P2,则有

(2)
其中可设
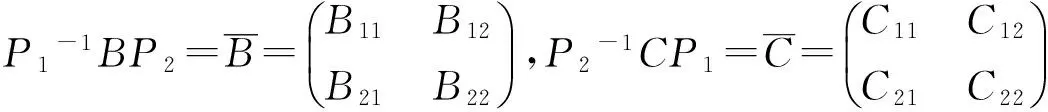
(3)
而
B11∈Rr×t,B12∈Rr×(s-t),B21∈R(n-r)×t,B22∈R(n-r)×(s-t),
C11∈Rt×r,C12∈Rt×(n-r),C21∈R(s-t)×r,C22∈R(s-t)×(n-r).

在本文中,我们主要研究(1)式中的矩阵所确定的方程Gk=λG(k=2,3)有解的充要条件,以及相应的一些性质.
2 对角线元为幂等矩阵的2×2分块方阵的数量幂等性
本节运用了幂等矩阵的相关性质,并通过一系列的计算得到以下两个定理.

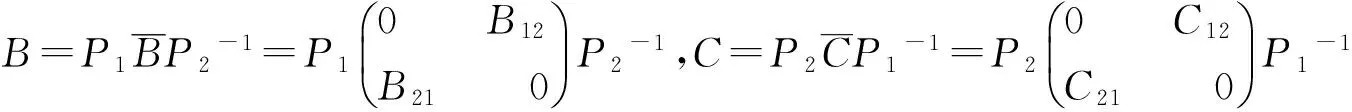
(4)
其中:B12,B21,C12,C21满足B21C12=0,B12C21=0,C21B12=0,C12B21=0;P1∈GLn(R),P2∈GLs(R).
或者λ=2,且

(5)
其中:B11,C11满足B11C11=Er,C11B11=Et;P1∈GLn(R),P2∈GLs(R).

(6)
由式(3)分别代入式(6)中各式,依次得到
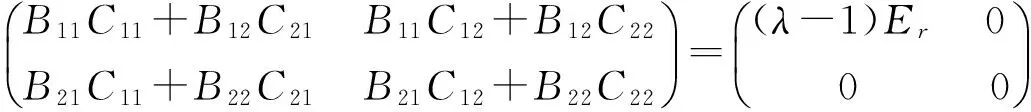
(7)
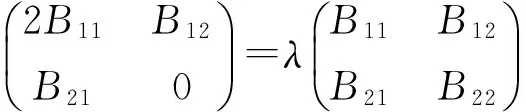
(8)

(9)

(10)

(11)

首先,当λ=1时,由(11)式得到B11=0,B22=0,C11=0,C22=0,将之代入式(7)和式(10),就得到
B21C12=0,B12C21=0,C21B12=0,C12B12=0 .
(12)

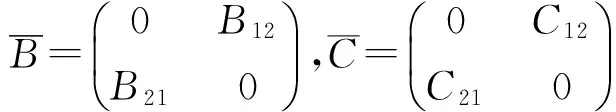
其中B12,B21,C12,C21满足式(12)条件.
其次,当λ=2时,同样由式(11)得到B12=0,B21=0,C21=0,C12=0,C22=0.将之代入式(7)和式(10),就得到
B11C11=Er,C11B11=Et.
(13)


其中B11,C11满足式(13)条件.
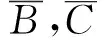
综上讨论可得,定理1结论成立.


(14)
其中,P1∈GLn(R),P2∈GLs(R),且Bij,Cij满足如下条件
B11C11=0,C11B11=0,B11C12=0,C11B12=0,C21B11=0,B21C11=0,B22=B22C22B22,C22=C22B22C22.
或者λ=4,且

其中:P1∈GLn(R),P2∈GLs(R),且Bij,Cij满足如下条件
(15)
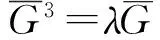
由式(3)分别代入式(16)、(19)、(17)和式(18),依次得到如下四个等式组
将(II1)中式(20)、(21)和(II2)中式(26)代入式(28)得到
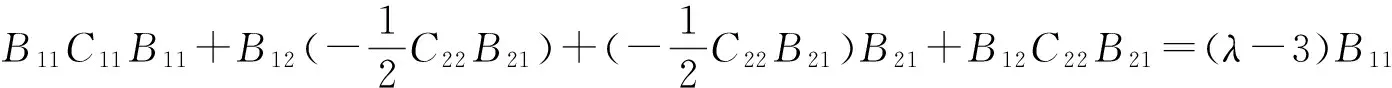
将(II1)中式(20)代入上式并整理得到

(36)
类似地,利用(II1)中式(21)和(II2)中式(25)、(27)代入式(29)并整理得到

(37)
利用(II1)中式(22)、(23)和(II2)中式(26)代入式(30)并整理得到
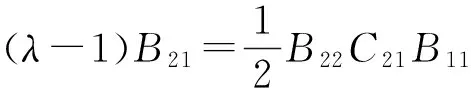
(38)
利用(II1)中式(22)、(23)和(II2)中式(27)代入式(31)并整理得到
λB22=B22C22B22.
(39)
因此等式组(II3)等价于
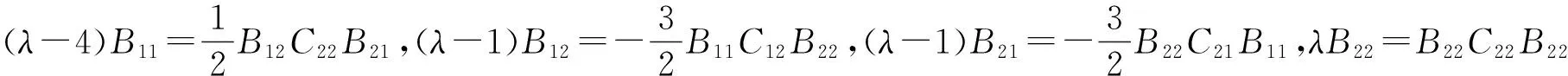
(40)
同理,利用(II1)和(II2)中的关系式,可以将等式组(II4)得到变为如下等价的等式

(41)
由于等式组(I)等价于四个等式组(II1)-(II4)因此等式组(I)等价与如下等式组(II)
下面对等式组(II)分λ=1,或λ=4,或λ≠1且λ≠4的情况讨论如下:
1)λ≠1且λ≠4,由(44)中第1式和(45)中第1式得到

(46)
由此得到
B11C11=0,C11B11=0,B11C12=0,C11B12=0.
(47)
将式(47)分别代入式(44)和式(45)中的第2和第3式,得到
B12=0,B21=0,C12=0,C21=0.
(48)
由此及式(46)得到
B11=0,C11=0.
(49)
将式(48)和式(49)分别代入式(42)和式(43)中的第1式,得到如下两个矛盾方程
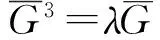
2)当λ=1时,由(44)和(45)中第1式得到
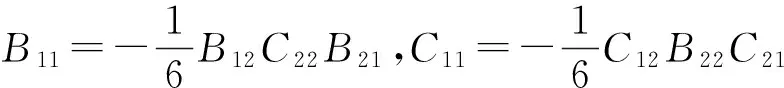
(50)
注意到式(42)和式(43)中B21C22=0,C21B12=0,由此及式(50)得到
B11C11=0,C11B11=0,B11C12=0,C11B12=0,C21B11=0,B21C11=0.
(51)
注意到式(42)和式(43)中有B12C22=-2B11C12,C12B22=-2C11B12,由此及式(50)、式(51)得到
B11=0,C11=0.
(52)
因此方程(II)等价于
也即G3=λG成立时有本定理中λ=1时的结论成立.
3)当λ=4,类似2)的讨论,可得到式(5)的结果.
[1]Hall F J. Generalized inverses of a bordered matrix of operators[J].SIAM J. Appl. Math., 1975, 29:152-163.
[2]章里程,廖祖华.分块矩阵加权Moore-Penrose逆的块独立性[J].数学杂志,2010,30(5):921-925.
[3]郭文彬,刘永辉,魏木生. 分块矩阵g-逆的块独立性[J].数学学报,2004,47(6): 1205-1212.
[4]YonggeTian.Rankequalitiesforidempotentandinvolutorymatrices[J].LinearAlgebraandApplications. 2001, 335: 101-117. [5]吴炎,王鸿绪.环Z/pkZ上s次幂等矩阵及矩阵的加权广义逆[J].大学数学,2004,20(6):55-59.
[6]杨忠鹏,傅丹娟,陈梅香.m次数量幂等矩阵线性组合的可逆性[J].数学研究,2010,43(2):178-184.
[7]吴炎.局部环上幂等矩阵线性组合的广义逆之间的关系[J].纯粹数学与应用数学,2012,28(2):155-166.
[8]杨晓英,刘新.分块幂等矩阵广义schur补的性质[J].云南师范大学学报,2009,29(6):18-21.
[9]吴炎.相似变换下幂零矩阵的{2,3}-逆的表示式[J].琼州学院学报,2013,20(5):19-25.
[10]张宗杰,吴炎.对角线元为数量幂等矩阵的上三角矩阵及其应用[J].西南师范大学学报(自然科学版),2016,41(8):6-11.
(编校:曾福庚)
Scalar-idempotent Properties of 2×2 Square Matrix of All Diagonal Elements in the Set of Idempotent Matrices
YU Ming-ming, WU Yan
(Department of Mathematics, Hainan Tropical Ocean University, Sanya Hainan 572022, China)
Let G be the 2×2 square matrix whose diagonal elements are idempotent matrices. By the matrix theory and methods, the k scalar-idempotent properties of the matrix G were studied, and the necessary and sufficient conditions for the existence of solution of equationsGk=λGwere obtained ,where k=2,3.
scalar-idempotent matrix; block matrix; scalar-idempotent property
2016-04-12
三亚市院地科技合作项目(2015YD24)
吴炎(1964-),男,海南乐东人,海南热带海洋学院教授,研究方向为代数矩阵论及其应用.
O151.21
A
1008-6722(2016) 05-0050-05
10.13307/j.issn.1008-6722.2016.05.10
