多核集群任务分配问题的0-1整数规划求解模型①

杨际祥 凌 玲

(重庆交通大学数学与统计学院 重庆 400074)



多核集群任务分配问题的0-1整数规划求解模型①

杨际祥②凌 玲

(重庆交通大学数学与统计学院 重庆 400074)

研究了典型多核集群任务分配中的节点内通讯特性。基于0-1整数非线性规划模型和线性松弛技术，给出了一种0-1整数线性规划任务分配问题求解优化模型。由于节点内的通讯量与通讯延迟较大，以最小化计算代价和节点间通讯代价为研究目标的传统求解模型具有严重的局限性，而该求解模型考虑了节点内通讯代价，并采用了线性规划松弛技术，其目标是最小化计算代价、节点间通讯代价和节点内通讯代价。计算结果验证了提出的模型的有效性。

多核集群， 任务分配问题(TAP)， 0-1整数规划， 线性规划松弛

0 引 言

任务分配问题(task allocation problem, TAP)是并行计算领域的一个经典问题，任务分配旨在将一组任务分配到一组计算节点上，以最小化总成本。总成本通常包括执行成本和节点间(或处理器间)通讯成本。然而，随着基于多核节点的以层次方式构成的集群成为并行计算的一种发展趋势，通讯成本不但包括节点间通讯成本，还应包括节点内通讯成本，而节点内通讯成本又与节点内的通讯量和通讯延迟两个因素密切相关。文献[1,2]通过通讯量和通讯延迟展示了节点内通讯的重要性。文献[1]指出，网络附属存储(NAS)基准测试中超过50%的通讯量是通过节点内通讯完成的。文献[2]研究表明，在典型的多核集群系统中，在节点内的通讯延迟与节点间的通讯延迟之比随消息的增大而增大。因此，考虑并优化节点内通讯与优化节点间通讯成本同等重要。传统的任务分配问题(TAP)求解以最小化节点计算代价与节点之间的通讯代价为研究目标，具有严重的局限性。

现有的求解TAP的方法大致可分为三类，即图理论法、数学规划法以及启发式方法[3]。数学规划方法将任务分配问题转化为优化问题，并使用数学规划技术[3,4]进行求解。如果未知变量为整数，则该问题为整数规划问题。在实际情况中，通常未知变量个数有限，该问题为一NP难问题。0-1整数规划为整数规划的一种特殊情况，变量或为0或为1，该问题仍为一NP难问题。传统的四个或者更多个计算机上的任务分配问题的求解为一NP完全问题，更不必说新的多核集群任务分配问题(task allocation problem in multi-core clusters，TAPMC)的求解为一难解问题。本文使用整数规划理论求解TAPMC，首先给出一个0-1整数非线性规划求解模型，然后借助线性规划松弛技术与优化方法给出一种新的0-1整数线性规划模型。

1 传统TAP的0-1整数规划模型

不失一般性，假设n个任务分配到m个计算节点上，部分任务间彼此存在通讯。如果任务i被分配到计算节点j上，产生的执行成本设为eij，而设当任务i与任务k未被分配到同一个计算节点上产生的通讯成本为cik。二元变量xij定义为1，当且仅当任务i分配到计算节点j上，反之为0。传统任务分配问题可转化为0-1整数规划问题，该0-1整数规划问题旨在最小化完成任务的总成本，如模型

(1)

所示。

0-1整数规划问题可分为整数规划问题或者非线性规划问题，部分研究者给出了该问题的求解方法。基于分枝限界技术，文献[5]给出了一种求解该问题的方法。文献[6]使用Lagrangian对偶公式分枝限界法给出了一种有效的求解算法；文献[7,8]给出一种解决整数规划问题的列生成模型，并且证明了它们的计算性能；文献[4]引入一种混合整数规划模型，当存在大量的任务通讯时尤其有效，求解大规模问题时比其它精确算法更为有效。

2 多核集群任务分配问题(TAPMC)求解模型

2.1 0-1整数非线性规划模型

0-1整数规模划型(式(1))能够有效求解传统任务分配问题，但无法有效求解多核集群任务分配问题。在本文中，考虑了多核集群任务分配问题的0-1整数规划问题，给出多核集群任务分配问题的一种0-1整数非线性规划求解模型，如模型

(2)

所示。

在模型式(2)中，目标函数包括以下三个部分：

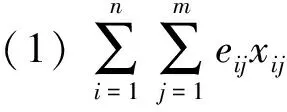
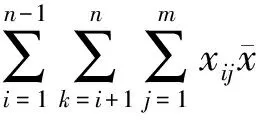
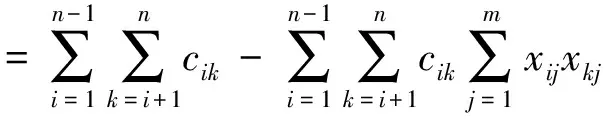
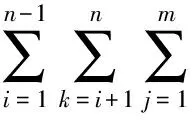
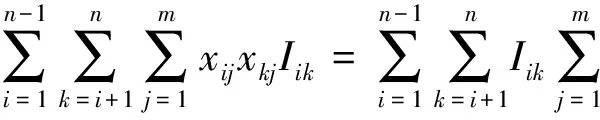
为有助于求解TAPMC问题，模型式(2)可表示为

(3)

2.2 0-1线性整数规划模型

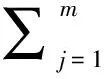
(4)

进一步，引入变量uij与vij。若任务i未分配到计算节点j，则uij(或者vij)为0，否则表示任务i与其它任务(任务i+1,i+2,…,n)之间发生的节点间(或者节点内)通讯总成本。因此，模型式(4)可表示为

(5)

2.3 应用极大独立集优化TAPMC求解模型

尽管给出了求解TAPMC的0-1整数线性规划模型，该模型仍需进一步优化。在计算节点内与节点间的通讯成本时，假定通讯图为一完全图，因此可能产生一些不必要的计算。为避免这些不必要的计算，引入极大独立集理论以优化通讯成本的计算。

定义1：对于一个无向图G=(V,E)及子集S(S⊂V)，若：(1) S中的任意两个节点不相邻，则称S为G的一个独立集；(2) S为G的一个独立集，且对任意v∈V-S，在S中至少存在一个节点邻接v，则称S为G的一个极大独立集。

图1 调整前的通讯图与通讯矩阵

图2 调整后的通讯图与通讯矩阵

在算法1中，swap(i, j)方法完成第i行与第j行之间的数据交换操作，同时完成第i列与第j列之间的数据交换操作。

3 计算结果

任务间的通讯使得分配决策比较困难。传统的任务分配问题的解决方法在任务间存在较少通讯时比较有效，而在解决涉及大量的任务间通讯(如通讯密度为50%、75%或100%)情形时显得较为困难。文献[4]引入了一种任务分配问题整数求解模型U2,且计算结果表明其在当所求解问题存在大量的任务间通讯成本时效果较好。因此，通过与U2计算结果比较，以研究本文模型的有效性。

计算节点具体环境为Intel(R) Core(TM)2 Quad CPU Q6000 @2.40GHz,8G内存,L2 Cache 4M, L1 Cache 32KB;Windows Server 2003;CPLEX 9.0[9]。任务数n配置为100,150,200；计算节点数m配置为4,6,8,10；通讯密度配置为50%,75%,100%。

计算结果如图3～图5所示。在任务数n=100,150,200时，本文模型的求解时间皆快于U2，且随任务间通讯密度的增大，本文模型的优势更加明显。此外，当n=150,m=10，通讯密度=100%；n=200，m=8,10，通讯密度=50%, 75%；n=200,m=6,8,10，通讯密度=100%时，模型U2计算效率低下(超时)，而本文模型则表现出了良好的计算效率与可扩展性。

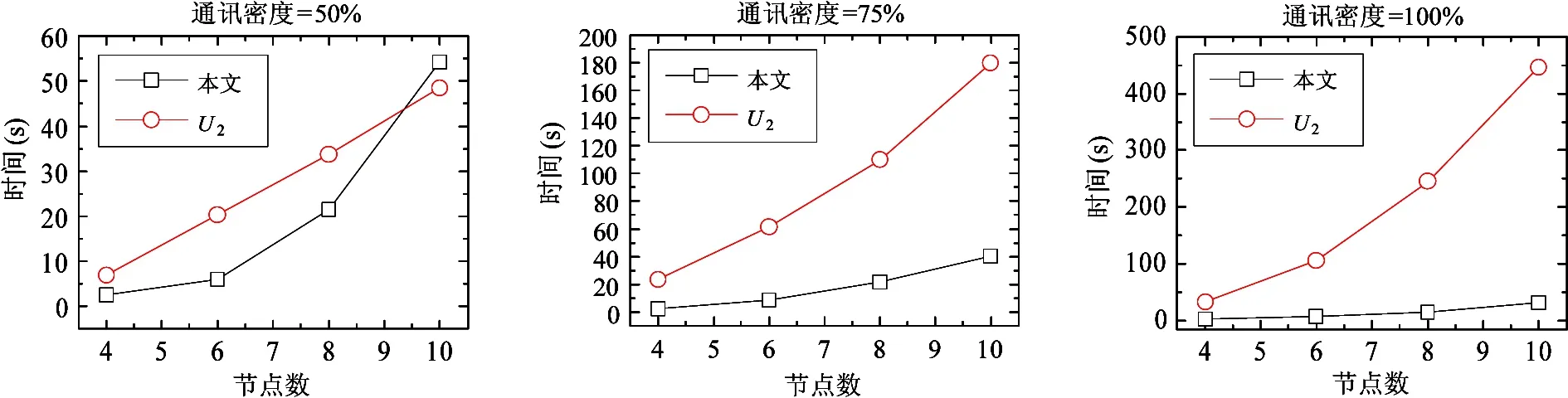
图3 不同通讯密度下的任务(任务数n=100)求解时间随节点数的变化关系

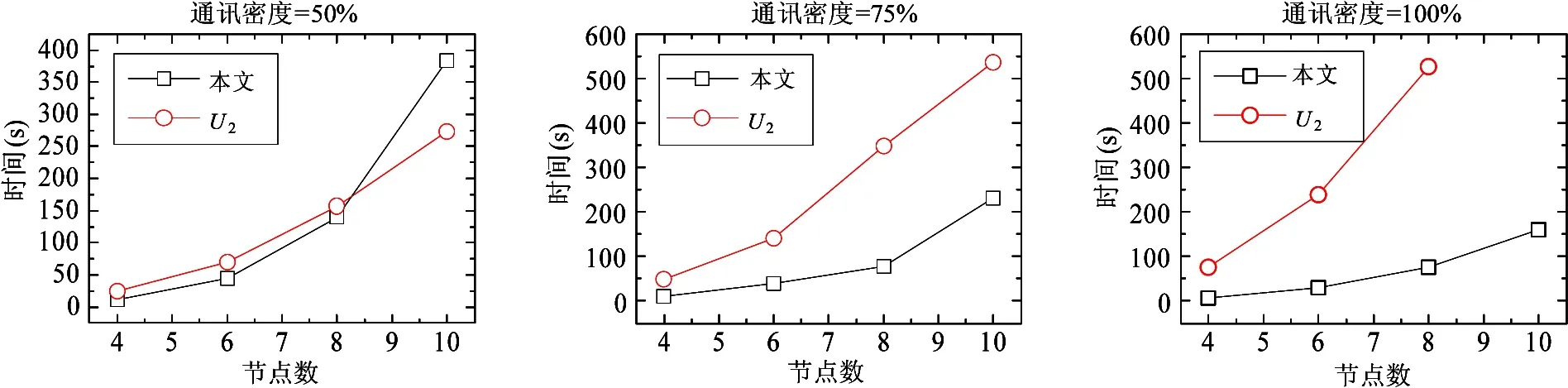
图4 不同通讯密度下的任务(任务数n=150)求解时间随节点数的变化关系

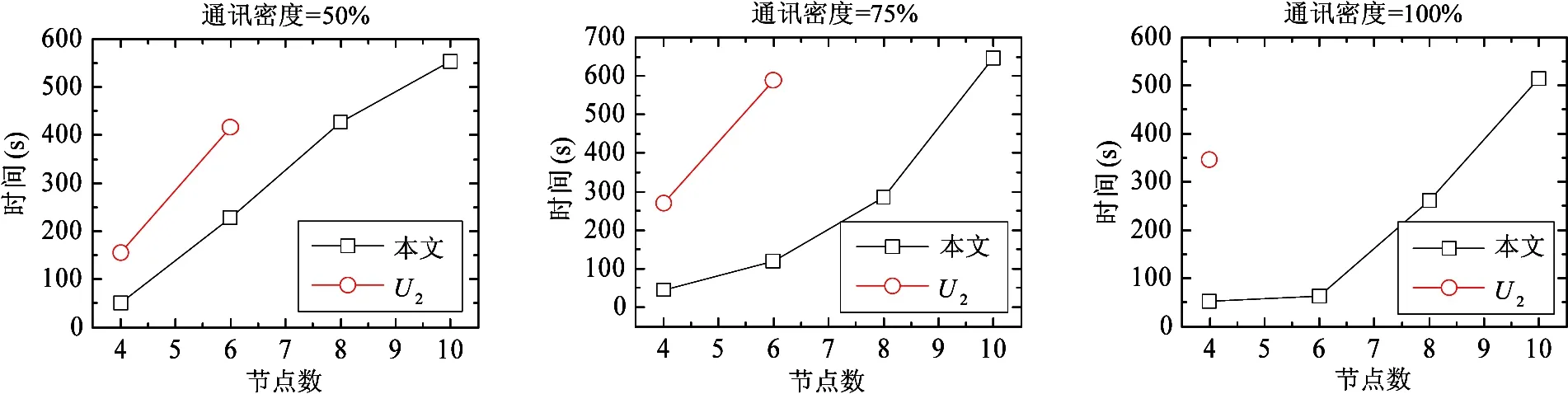
图5 不同通讯密度下的任务(任务数n=200)求解时间随节点数的变化关系

4 结 论

任务分配是多核集群系统中的一个重要问题。传统TAP为NP难问题,新的TAPMC的求解更具有挑战性。本文给出一种求解TAPMC的0-1整数非线性规划模型,并给出一种0-1整数线性规划模型及其优化方法。计算结果表明,当存在大量任务间通讯时,本文给出的计算模型比较有效。

[1] Chai L, Gao Q, Panda D K. Understanding the impact of multi-core architecture in cluster computing: a case study with Intel dual-core system. In: Proceedings of the 7th IEEE International Symposium on Cluster Computing and the Grid, Rio De Janeiro, Brazil, 2007. 471-478

[2] 涂碧波，邹铭，詹剑锋等. 多核处理器机群Memory层次化并行计算模型研究. 计算机学报, 2008, 31(11): 1948-1955

[3] Ernst A, Jiang H, Krishnamoorthy M. Exact solutions to task allocation problems.ManagementScience, 2006, 52(10): 1634-1646

[4] Menon S. Effective reformulations for task allocation in distributed systems with a large number of communicating tasks.IEEETransactionsonKnowledgeandDataEngineering, 2004, 16(12): 1497-1508

[5] Soylu B. Heuristic approaches for biobjective mixed 0-1 integer linear programming problems.EuropeanJournalofOperationalResearch, 2015, 245(3): 690-703

[6] Sherali H D, Smith J C. Higher-level RLT or disjunctive cuts based on a partial enumeration strategy for 0-1 mixed-integer programs.OptimizationLetters, 2012, 6(1): 127-139

[7] Alfandari L, Sadki J, Plateau A. Hybrid column generation for large-size covering integer programs: application to transportation planning.Computers&OperationsResearch, 2013, 40(8): 1938-1946

[8] Rönnberg E, Larsson T. All-integer column generation for set partitioning: basic principles and extensions.EuropeanJournalofOperationalResearch, 2014, 233(3): 529-538

[9] ILOG, Inc. ILOG CPLEX 9.0 User’s Manual. 2003, http://eaton.math.rpi.edu/cplex90html/pdf/usrcplex.pdf

A model for solving task allocation problems in multi-core clusters using 0-1 integer programming

Yang Jixiang, Ling Ling

(School of Mathematics and Statistics, Chongqing Jiaotong University, Chongqing 400074)

The in-node communication characteristics of the task allocation of multi-core clusters was studied. An optimized model for solving task allocation problems in multi-core clusters using 0-1 integer linear programming was proposed based on the 0-1 integer linear programming model and the linear relaxation technique. Considering that the traffic and delay of in-node communications are bigger, which brings serious limitations to the traditional models aiming to minimize the computing cost and the cost of the node-node communications, the proposed model takes account of the cost of in-node communications and adopts the technique of linear programming relaxation, with the aim to minimize the computing cost, the cost of node-node communications, and the in-node communication cost. The effectiveness of the model is verified by the computation result.

multi-core cluster, tast allocation problem, 0-1 integer programming, linear programming relaxation

10.3772/j.issn.1002-0470.2016.04.003

①国家自然科学基金(11401061)，重庆市自然科学基金(KJ1400316)和交通运输部建设科技基金(2014318223030)资助项目。

2015-12-16)

②男，1975年生，博士，副教授；研究方向：并行计算与系统可靠性等；联系人，E-mail: jixiang_yang@126.com(