静电地板耦合强度及成形分析

王军领，詹俊勇，仲太生，罗素萍

（扬力集团股份有限公司，江苏扬州225127）

静电地板耦合强度及成形分析

王军领，詹俊勇，仲太生，罗素萍

（扬力集团股份有限公司，江苏扬州225127）

建立静电地板中混凝土的本构模型，采用损伤塑性模型建立静电地板的耦合模型，对圆弧形和圆锥形两种结构进行有限元耦合强度分析，对比找出强度、刚度更好的结构。最后对两种结构进行成形分析，找出成形工艺更好的结构，最终提供一种成形工艺好、强度高的结构。

耦合强度分析；地板；成形分析；混凝土强度

静电地板上下表面的材料为普通合金钢板经冲压而成，其材料特性为弹性线性变形。组装时将上下合并，通过螺栓拉紧固定，并将中间空腔部分充满水泥材料。测试强度时，将底面四周固定，上面中间区域加载应力，当破坏时，水泥材料首先破坏。所以本文分析中水泥的材料特性极其关键。

1 静电地板混凝土本构模型

混凝土在高压下（三轴）表现出准脆性的行为，不同于普通的脆性材料，混凝土可以有非弹性变形，非弹性变形可以比弹性变形大很多。混凝土损伤机制：①混凝土内部微裂纹和微孔洞的产生和发展；②在高压（静水压力）下材料的固化和多微孔的结构的坍塌；③混凝土的材料属性。

混凝土材料屈服后的行为主要考虑拉伸开裂和压缩破碎而破坏。屈服或破坏面的演化由两个变量εtpl（拉伸等效塑性应变）和εcpl（压缩等效塑性应变）控制。其中混凝土的本构模型如图1、2所示。在弹性阶段，该模型采用线弹性模型对材料的力学性能进行描述，进入损伤阶段后，模型损伤后的弹性模量可以表示为损伤因子d和初始无损弹性模量的关系如式（1）所示。

式中：E0为初始（无损）弹性模量，d为损伤因子[1]。

图1 混凝土单轴拉伸应力应变曲线

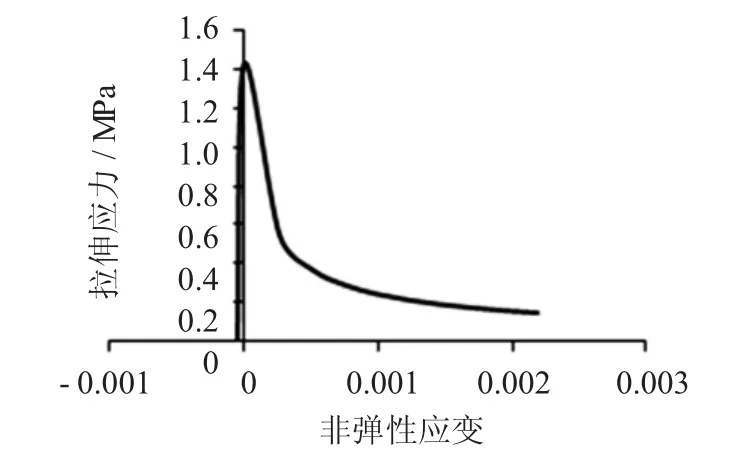
图2 混凝土单轴压缩应力应变曲线

损伤因子应通过试验取值，但一般情况下可按式（2）求得损伤因子的数值：

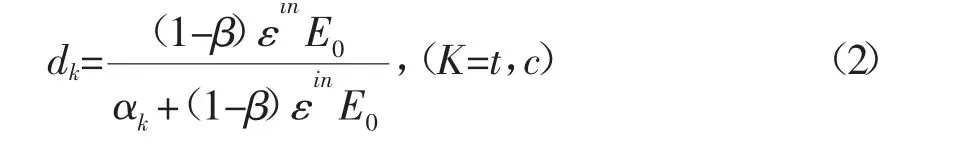
式中：t，c——分别代表拉伸和压缩；

B——塑性应变与非弹性应变的比例系数，受压时取0.35～0.7，受拉时取0.5～0.95；

εin——混凝土拉压情况下的非弹性阶段应变。

从以上可知，拉伸最大应变为0.00219时，相应的真实应力为0.144MPa，当材料的Mises应变达到0.00219后，材料变为理想塑性，即材料会持续变形。换言之，在理想塑性状态下，应力和应变值不是一一对应的，而这有可能造成收敛问题[2]。

2 静电地板耦合强度

单调荷载作用下，弥散开裂模型和损伤塑性模型均能较好地描述钢筋混凝土中混凝土的力学行为，采用这两种模型进行钢筋混凝土非线性分析，所得的计算结果是可信的。但损伤塑性模型的使用范围更广，还能运用于循环和动力荷载的隐式和显式分析[3]，本次分析采用损伤塑性模型。

2.1 耦合模型的建立

此次分析中混合使用了弹塑性材料和线弹性材料。为缩短计算时间，特将水泥混凝土设置为弹塑性材料，将外壳和辅助块设置为线弹性材料，外壳和混凝土的力学行为通过粘结强度建立[4]。

若最大主应力（拉应力）大于混凝土的抗拉强度，则认为混凝土开裂，通过显示最大主应力的法线方向，可以大致表示出裂缝的开裂方向。利用最小主应力，可以查看实体中残余应力的大小[5]。

此静电地板为对称结构，故取1/4模型进行模拟，并将对称面处加载对称约束，如图3、4所示，并定义混凝土和上下两层钢板的本构关系[6]。

2.2 圆弧形耦合强度计算结果

由图1、2可知，混凝土的最大拉应力为1.43MPa，最大压应力为14.3MPa。所以当给面积为160mm×160mm的辅助块一个0.3MPa的压强，即载荷为768kg时，对图5中的圆弧形模型进行耦合强度分析。

图3 力加载和对称面加载模型

图4 固定和对称面加载模型

图5 圆弧形模型

图6 载荷768kg下最大拉应力

由图6可知，混凝土部分最大拉应力为1.319MPa，最大应力处的应变为2.7e-5，已经接近混凝土的最大抗拉强度。所以此时已经接近静电地板承受力的最大极限值。

在工程结构中，等效塑性应变一般不应超过材料的破坏应变[7]，通过单轴试验可知，当超过某应力水平，混凝土表现非线性行为，表现出累积不可修复的损伤直到发生破坏。

2.3 圆锥形耦合强度计算结果

同样给面积为160mm×160mm的辅助块一个0.3MPa的压强，即载荷为768kg时，对图7中的圆锥形模型进行耦合强度分析[8]，计算出静电地板中混凝土的最大拉应力如图8所示。

极限变形准则以材料、截面或构件的极限应变、变形或延性作为破坏的界限条件，当应变、变形（位移和转角）或延性大于极限阈值时认为材料、截面或构件发生破坏，能较好地反映和区分结构屈服后的性能及破坏程度。结构倒塌破坏的本质是材料的失效断裂破坏，故上述破坏准则中，基于材料层次的极限变形准则（极限应变准则）能够较好地描述结构倒塌破坏的本质，其破坏阈值仅与材料自身性能有关，且容易通过试验测定[9-10]。

图7 圆锥形模型

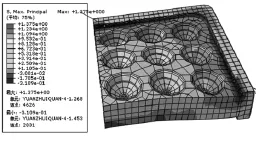
图8 载荷435.2kg下最大拉应力

3 静电地板成形分析

对圆弧形结构和圆锥形结构进行成形有限元分析，两种结构的成形极限图如图9、10所示。

通过上述两图成形分析，圆锥绿色区域多，黄色区域（容易拉裂区域）少，说明其成形质量好，便于成形；而圆弧形黄色区域相对较多，即容易拉裂区域相对较多，成形质量差，危险区域大，不利于组装成品后模型的受力。但由于分析建模时无法保证完全符合成形后板厚，所以有限元模型采用等厚的0.5mm钢板。考虑成形质量优劣的条件下，两种模型装配完成后的刚度和强度应该需要进一步的考虑，但显而易见的是，如果存在拉裂缺陷，必定会降低静电地板的整体强度和刚度，所以可以稍微损失其强度，采用圆锥形结构的模型方案。

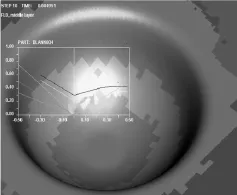
图9 圆弧形成形分析

图10 圆锥形成形分析

4 结语

（1）本文混凝土的破坏采用损伤塑性模型，混凝土单轴拉伸和压缩损伤塑性部分的力学行为则由损伤塑性描述。所有有限元分析软件材料库中的混凝土损伤塑性模型是一种通用的混凝土材料模型，该模型通过拉伸应力应变关系、压缩应力应变关系和损伤因子等来模拟混凝土非线性行为，取得了较为满意的计算结果。

（2）对两种形状模型进行耦合非线性有限元分析，计算出各自在同等载荷下的应力应变云图结果，通过对比得出在同等厚度下，圆弧形结构比圆锥形结构强度好。

（3）为查看两种形状的成形结果，分别对两种结构进行成形有限元分析，并对比成形后的极限图可知，圆锥型结构成形效果更好，如果圆弧形状在成形过程中存在拉裂缺陷，也会降低其承载强度和刚度，故可以损失一些强度，做成圆锥形状。

[1]张劲，王庆扬，胡守营，等.ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构，2008，（8）：127-130.

[2]石亦平，周玉蓉，著.ABAQUS有限元分析实例详解[M].北京：机械工业出版社，2011.

[3]周小军.ABAQUS中弥散裂缝模型与损伤塑性模型的比较[J].福建建筑，2010，（5）：49-51.

[4]张国丽，苏军.基于ABAQUS的钢筋混凝土非线性分析[J].建筑技术，2008，（20）：5620-5624.

[5]王军领，郑翔，吴焕.圆柱滚子轴承动静态有限元分析[J].扬州大学学报（自然科学版），2012，（2）：43-46.

[6]王军领，詹俊勇，仲太生，等.组合式大型压力机横梁强度刚度分析[J].锻压装备与制造技术，2014，49（6）：26-29.

[7]王军领，郑翔，姚菁琳.高速压力机机身减振的研究[J].制造技术与机床，2013，（9）：72-76.

[8]王军领，詹俊勇，仲太生.传动间隙对高速压力机下死点重复精度影响分析与测试[J].锻压装备与制造技术，2013，48（3）：19-22.

[9]郝中华.基于有限元的钢筋混凝土框架结构倒塌分析[D].沈阳：沈阳建筑大学，2014.

[10]王军领，詹俊勇，仲太生，等.高速压力机齿轮啮合强度分析[J].机械工程与自动化，2015，（3）：96-100.

Analysis of coupling strength and form ing process for electrostatic floor

WANG Junling，ZHAN Junyong，ZHONG Taisheng，LUO Suping
（Jiangsu Yangli Group Co.,Ltd.,Yangzhou 225127,Jiangsu China）

The constitutive model of concrete in electrostatic floor has been established.The damage plasticity model has been built to the coupling model of electrostatic floor.The finite element coupling strength of circular and conical structure have been analyzed.The structure with better strength and rigidity has been found out by comparison.The forming analysis has been conducted to the two structures.The structure with better forming process has been obtained.Finally,the structure with good forming process and high strength has been provided.

Coupling strength analysis;Floor;Forming analysis;Strength of concrete

TG315.5

B

10.16316/j.issn.1672-0121.2016.05.021

1672-0121（2016）05-0071-03

2016-05-24；

2016-06-15

王军领（1985-），男，工程师，硕士，从事机械结构自动化设计等研究。E-mail：w756251@163.com