可验证模指数批计算外包方案
2016-12-06黄春水任艳丽蔡建兴
黄春水,任艳丽,蔡建兴
(上海大学通信与信息工程学院,上海 200444)
可验证模指数批计算外包方案
黄春水,任艳丽,蔡建兴
(上海大学通信与信息工程学院,上海 200444)
随着云计算的发展,如何将一些耗时的计算任务安全地外包给不受信任的云服务器引起了人们的广泛关注.目前的模指数运算外包方案大多基于两个不可信的服务器,或者外包结果的可验证概率不高.因此,使用随机置换方法,提出了一个新的模指数批计算外包方案.模指数运算的底数和指数对于服务器都是保密的,并且用户的可验证概率接近于1.与已有方案相比,所提方案基于单个不可信服务器实现了输入数据的隐私性,并提高了外包结果的可验证概率.对所提方案进行了模拟实验,测试结果表明外包方案极大地降低了用户的计算代价.
云计算;外包方案;可验证;模指数运算
随着云计算[1]的兴起,外包计算引起了人们广泛的关注.通过外包计算,计算能力有限的客户可以将任务外包给云服务器,这将为那些资源受限的设备节省大量的计算时间.同时,外包计算也面临着许多挑战[2-3],对安全性有很高的要求.云服务器并不是完全可信的,有可能存在泄露用户的信息,或故意返回错误结果的情况,而可验证计算(Verifiable Computation,VC)[4]方案很好地解决了这个问题.通过可验证计算方案,用户的信息都是对服务器保密的,并且服务器返回的任何错误结果都将不能通过验证.
模指数运算是密码系统中最常见的、最为耗时的运算之一.许多公钥加密、数字签名方案[5]需要用到模指数运算,研究如何实现模指数安全外包计算具有重要的现实意义.文献[6]定义了第一个外包计算安全模型,并且基于两个不可信的服务器,提出了单个模指数运算外包算法.文献[7]提出了新的模指数运算外包方案,在计算效率与可验证率方面都要优于文献[6]的.尽管文献[6-7]中的方案实现了指数与底数的隐私性,但它们都需要进行大量复杂的预计算操作,效率不高,并且遇到恶意的服务器时,用户检测出错误的概率也都不是很高,文献[6-7]的可验证率分别为1/2、2/3.文献[8]提出了多个模指数相乘的外包计算方案,与文献[6-7]比,文献[8]只用了一个服务器,也同时实现了指数与底数的隐私.但是,由于文献[8]的方案是针对多个模指数相乘的外包计算方案,在单个模指数外包方面效率远低于文献[6-7]的,并且遇到恶意的服务器时,文献[8]的可验证率也仅有1/2.文献[9]提出了基于单个服务器的批量模指数外包方案,与文献[6-8]相比,文献[9]的方案不需要复杂的预计算操作,因此在批量外包计算模指数方面效率更高,且可验证概率接近于1.但是,文献[9]的方案在隐私性方面有明显的缺陷,不能同时实现指数和底数的隐私性.
笔者使用随机置换方法,提出了一个新的模指数批计算外包方案.方案基于单个服务器,同时实现了底数和指数的隐私性.当服务器不诚实时,外包用户能以接近于1的概率检测到错误.与同类方案相比,笔者提出的方案仅需少量的预计算操作,效率优于文献[6-8]中的方案,稍逊于文献[9]中的方案.但是与文献[9]相比,笔者提出的方案同时实现了指数和底数的隐私性,安全性高于文献[9]中的方案.
1 笔者提出的方案
在笔者提出的方案中,用到了一个被称为Rand[6]的子程序,用于产生随机数对.Rand子程序的输入是素数p、q,底数,且满足q|p-1,输出(a,gamod p),其中.目前,实现这一Rand子程序有两种方式:一种方式是预先使用一个可信任的服务器,产生形如(a,gamod p)的随机数对组成表,然后将这张表加载到客户端T的内存中去,每次调用Rand子程序,T就从表中随机取出一个随机数对,这种方式因此被称为查表法.另一种就是用EBPV发生器[10]产生独立的随机数对,这种方式可以抵挡敌手自适应的攻击,一个n比特的指数运行的时间复杂度为O(log2n).
1.1可验证模指数计算方案
可验证模指数计算方案是一个基于可信的客户端T与不可信的服务器端U的双方协议.T提供底数u和指数x作为输入,经盲化操作后,再发送给U.最后,U返回计算结果和一个验证值.用户利用服务器返回的验证值验证服务器返回的计算结果的正确性.一般的可验证模指数计算方案都包含3个算法:
(1)(σu,σx)←Prob Gen(x,τ,u).输入指数x、秘密输入τ和底数u,输出盲化后的指数σx和盲化后的底数σu.
(2)σy←Com pute(σu,σx).输入σx和σu,输出盲化后的模指数计算结果σy.
(3){y,⊥}←Verify(σy,τ).输入盲化后的模指数计算结果σy,完成正确性证明.若验证结果正确,输出计算结果y=ux;否则,输出⊥.
1.2可验证模指数批计算外包方案
可验证模指数批计算外包算法是在一个不可信的服务器上实现的.输入输出,其中p、q是两个大素数,且满足q|p-1.笔者提出的外包方案包含3个子算法,如下所示.
算法1 Prob Gen((x1,x2,…,xt),τ,u).
T调用Rand子程序,产生3个随机数对(α,gα),(β,gβ),(a,ga),然后从中选取两个随机数b,b′.定义τ={(α,gα),(β,gβ),(a,ga),b,b′},v=gαmod p,μ=gβmod p,γ=gamod p.
然后,客户端T利用秘密输入τ对底数u与指数xi进行盲化处理.
最后输出盲化后的指数σx={A,D}和盲化后的底数σu={g,w}.将(σu,σx)={(D,g,p),(A,w,p)}发给服务器.
算法2 Compute(σu,σx).
U利用T发过来的σu、σx计算出结果σy,并将它发回给客户端.
利用T传过来的(D,g,p),(A,w,p),U完成计算并返回对应的查询结果:
算法3 Verify(σy,τ).
T接收到从服务器U传过来的σy集合后,进行如下操作来验证U返回的计算结果的有效性:
(1)T从σy中取出,其中,1≤k≤t.
(2)T从σy中取出,其中,1≤k≤t.

如果对于所有的i∈[1,t],上面的验证等式(1)都成立,那么输出;否则,输出⊥.
2 方案分析
使用与文献[6-7]相同的安全定义,从理论上证明笔者所提方案的正确性和安全性.受篇幅限制,相关安全定义不再给出,具体安全定义和模型见文献[6-7].
2.1正确性
通过以下引理证明方案的正确性,即只要服务器是诚实的,通过以上笔者提出的方案总能够得到正确的计算结果y=uxi且式(1)成立.
引理1 如果服务器是诚实的,则y=uxi且式(1)成立.
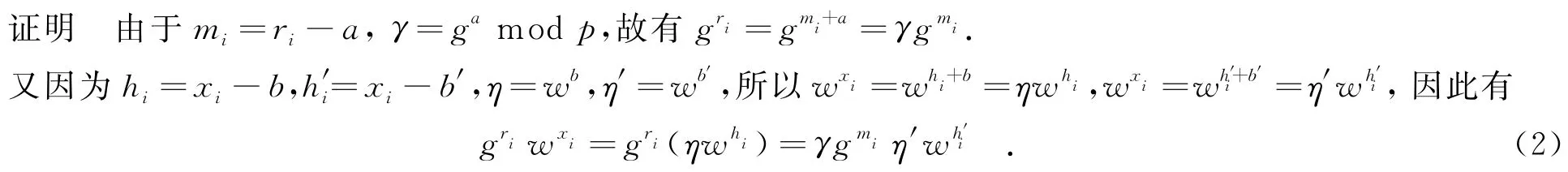
由式(2)可知,只要服务器是诚实的,则式(1)成立.

2.2安全性
通过以下两个引理证明方案的安全性.
引理2 基于单个不可信服务器模型,算法(T,U)是外包算法BExp的λ安全外包的实现.其中,输入(x1,x2,…,xt;u)可能是可信任的秘密输入,或是可信任的受保护的输入,或是敌手的受保护的输入.
证明 首先,证明EVIEWreal~EVIEWideal.如果输入{(xi;u):1≤i≤t}不是可信的秘密输入,E总能知道输入信息.显然,这种情况下模拟器S1执行过程将与实际的环境相同.因此,只需考虑输入{(xi;u): 1≤i≤t}是可信任的秘密输入的情况.
在理想的实验环境中,模拟器S1执行过程如下:当接收到第i个输入时,S1忽略它们,并向U′提交4t个形如的查询操作.然后,S1随机检测2t个输出:如果有一个错误被检测出来,输出“error”,indi=1(ind表示是否发现错误,如果发现则为1;否则为零);如果没有错误被检测出来,S1继续检查其他2t个输出;如果所有的输出都通过检测,S1输出,indi=0;否则,S1挑选t个随机数z1,z2,…,zt,并输出.在上面的所有情况中,模拟器S1都要保存它自己的所有状态.U′的输入分布在实际和理想的实验环境中,在计算上都是不可区分的.在理想实验环境中,所有的输入都是随机选取的.在实际实验环境中,由于T在向U提交查询请求操作之前,所有指数已经过一个映射函数加密扰乱,因此两次查询操作的过程是独立随机的,在计算上不可区分.
接下来证明UVIEWreal~UVIEWideal.如果输入{(xi;u):1≤i≤t}不是可信的秘密输入、可信的受保护的输入和敌手的受保护的输入时,U′总能知道输入信息.显然,这种情况下模拟器S2执行过程将与实际的环境相同.因此,只需考虑输入是可信的秘密输入、可信的受保护的输入和敌手的受保护的输入时的情况.
在理想的实验环境中,模拟器S2执行过程如下:当接收到第i个输入时,S2忽略它们,并向U′提交4t个形如的查询操作,然后保存自己和的所有状态.同上面证明的过程一样,U′的输入分布在实际和理想的实验环境中在计算上都是不可区分的.因此,尽管通过indi的值E能够很容易地区别真实环境和理想环境,但是E不能把这一信息传递给U′.所以,有UVIEWreal~UVIEWideal成立.
引理3 在单个服务器恶意模型中,算法(T,U)是外包算法BExp的(O((6t+log2n)(nt)),(4t2-1)(4t2),λ)安全外包的实现.
证明 用平方乘算法计算一个模指数形如uamod p,大概需要1.5n次的模乘运算,其中n表示指数a的比特长度.因此,用平方乘算法直接计算t个指数大概需要进行1.5nt次模乘运算.而用BExp算法计算t个指数,需要1次模逆运算,6t+1次模乘运算.另外,还调用了3次Rand子程序.在1.1节中提到过如果使用EBPV发生器来实现Rand子程序,那么一个n比特的指数运行的时间复杂度为O(log2n).所以,算法BExp的时间复杂度为O((6t+log2n)(nt)).
在算法2中,用户T向服务器提交了两次查询操作,每次计算的模指数长度为2t.这两次查询的结果影响着算法3的最终验证结果.假设某次外包计算过程中U向T返回了一个错误的结果,要想通过算法3的验证使用户T接受这个错误的结果,U必须选取2个合适的数字,代替算法2产生的两个结果集合中的某两个数.但由于算法2中两次查询操作在计算上是不可区分的,并且查询操作前输入已经通过映射函数扰乱,所以替换成功的概率为1/(4t2).即U给T返回了一个错误的计算结果,最终被T检测出来的概率为(4t2-1)(4t2)(在下面的3.2节实验中,t取的都是10 00以上,可验证率接近于1).所以,算法BExp的可验证率为(4t2-1)(4t2).
综上所述,可以说算法(T,U)是外包算法BExp的(O((6t+log2n)(nt)),(4t2-1)(4t2),λ)安全外包的实现.
3 性能分析
3.1理论分析
假设将t个底数相同、指数不同的模指数外包给云服务器,统计出在不同方案中,客户T需要做的模乘运算次数、模逆运算次数、查询服务器的次数、隐私性状况、可验证率以及使用的服务器数量,如表1所示,其中m表示文献[4]中选取的随机数个数,m>100.

表1 模指数运算外包方案比较
根据表1,同文献[6-7]相比,笔者在实现用户的指数、底数都对服务器保密的同时,效率上有明显的提高.所做的模乘运算、模逆运算和查询服务器的次数都要少于文献[6-7]中的.随着外包模指数数量增多(t越大),这种效率的提升越明显.并且,笔者只用了一个服务器,可验证率也要高于文献[6-7]的.文献[8]虽然也只用了一个服务器并能够实现完全隐私,但在效率和可验证率上都不及笔者提出的方案.与文献[9]相比,尽管文献[9]的可验证率和服务器个数都与笔者提出的方案相同,甚至模乘运算、模逆运算和查询服务器的次数比笔者提出的方案少,效率方面比笔者提出的方案略高,但是,文献[9]不能实现用户的指数、底数同时对服务器保密,安全性方面不如笔者提出的方案.
3.2实验分析
首先,对笔者提出的方案进行实验,统计出外包不同数量的模指数时,用户端所需要的时间曲线图(如图1所示).由图1可知,采用笔者提出的外包方案,用户通过外包方案计算出结果的时间远小于用户直接计算的时间.并且,随着待外包模指数个数的增多,两者之间的时间差值增大,笔者提出的方案在大批量模指数外包方面的高效率特性更突出.
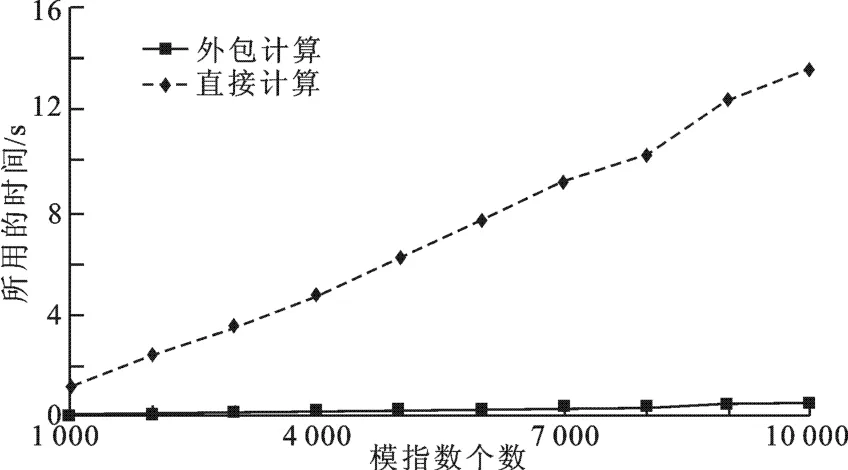
图1 外包模指数方案实验结果图
接着,分别对文献[7-9]的外包方案进行实验.一共测试了9组不同个数的模指数,统计用户端所需要的时间如表2所示.

表2 4种外包方案的计算时间 ms
根据表2,可以得出与3.1节相同的结论.在外包的模指数个数相同的情况下,文献[8]中方案所用的时间明显高于其他3种方案的,这是由于文献[8]中的方案主要是用于外包多个模指数乘法运算,所以在单个模指数外包上效率很低.笔者提出方案的时间介于文献[7,9]中方案之间,这也和3.1节方案分析的结论吻合.在外包的模指数个数相同情况下,与文献[7]中的方案相比,笔者提出的方案时间较少,这说明笔者提出的方案效率高于文献[7]的.随着外包的模指数个数增多,文献[7]中的方案和笔者提出方案的时间差值增大,这意味着在实现大批量的模指数外包上,笔者提出的方案效率的优势更明显.为了实现用户提供的指数、底数都对服务器保密,提高算法的安全性,笔者提出的方案进行了少量的预计算操作.牺牲用户少量时间换取了用户安全性的提高,这就导致了笔者提出方案的效率比文献[9]的低.
4 结束语
基于单个不可信服务器,提出了一种新的模指数批外包计算方案.与目前已知的模指数外包方案相比,笔者提出的方案仅需付出少量的预计算操作代价,便能够同时实现指数和底数的隐私性.在数据隐私的前提下,用户实现外包的效率高于其他算法.另外,外包结果的可验证概率较其他方案也有明显优势,如果服务器不诚实,用户检测出错误的概率接近于1.后续需改进的工作是:在保证用户外包效率不降低的情况下,尽可能地降低服务器的工作量.
[1]CHAPMAN C,EMMERICH W,MARQUEZ F G,et al.Software Architecture Definition for On-demand Cloud Provisioning[J].Cluster Computing,2012,15(2):79-100.
[2]REN K,WANG C,WANG Q.Security Challenges for the Public Cloud[J].IEEE Internet Computing,2012,16(1): 69-73.
[3]MEZGAR I,RAUSCHECKER U.The Challenge of Networked Enterprises for Cloud Computing Interoperability[J]. Computers in Industry,2014,65(4):657-674.
[4]GENNARO R,GENTRY C,PARNO B.Non-interactive Verifiable Computing:Outsourcing Computation to Untrusted Workers[C]//Lecture Notes in Computer Science:6223.Berlin:Springer,2010:465-482.
[5]江明明,胡予濮,王保仓,等.格上的代理重签名方案[J].西安电子科技大学学报,2014,41(2):20-24. JIANG Mingming,HU Yupu,WANG Baocang,et al.Proxy Re-signature Scheme over the Lattice[J].Journal of Xidian University,2014,41(2):20-24.
[6]HOHENBERGER S,LYSYANSKAYA A.How to Securely Outsource Cryptographic Computations[C]//Lecture Notes in Computer Science:3378.Berlin:Springer,2005:264-282.
[7]CHEN X,LI J,MA J,et al.New Algorithms for Secure Outsourcing of Modular Exponentiations[J].IEEE Transactions on Parallel and Distributed Systems,2014,25(9),2386-2396.
[8]WANG Y,WU Q,WONG D S,et al.Securely Outsourcing Exponentiations with Single Untrusted Program for Cloud Storage[C]//The 19th European Symposium on Research in Computer Security.Berlin:Springer,2014:326-343.
[9]MA X,LI J,ZHANG F.Outsourcing Computation of Modular Exponentiations in Cloud Computing[J].Cluster Computing,2013,16(4):787-796.
[10]NGUYEN P Q,SHPARLINSKI I E,STERN J.Distribution of Modular Sums and the Security of the Server Aided Exponentiation[C]//Progress in Computer Science and Applied Logic:20.Witzerland:Bikhauser Verlag AG,2001: 331-342.
(编辑:郭 华)
Verifiable outsourcing scheme for batch modular exponentiations
HUANG Chunshui,REN Yanli,CAI Jianxing
(School of Communication and Information Engineering,Shanghai Univ.,Shanghai 200444,China)
With the development of cloud computing,more and more people focus on how to outsource the expensive computations to the untrusted cloud servers.Currently,the outsourcing schemes for modular exponentiations are mostly based on two untrusted servers,or the checkability is very small.We propose a new outsourcing algorithm for batch modular exponentiations by using the random permutation.The exponent and the base are both private for the server,and the outsourcer can detect the error with probability close to 1.Compared with the previous algorithms,the proposed one is based on a single server, which realizes the privacy of inputs and increases the checkability of the outsourcing result.Finally,we simulate the proposed algorithm,and the experimental result shows that it can greatly reduce the computational cost for the outsourcer.
cloud computing;outsourcing algorithm;verifiable;modular exponentiation
TP309
A
1001-2400(2016)04-0135-06
10.3969/j.issn.1001-2400.2016.04.024
2015-04-14 网络出版时间:2015-10-21
国家自然科学基金资助项目(61202367);上海市自然科学基金资助项目(12ZR1443700);上海市教委创新基金资助项目(14YZ020)
黄春水(1991-),男,上海大学硕士研究生,E-mail:chunshui_h@163.com.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.048.html
