高斯形状上下文描述子

冯祥卫,冯大政,侯瑞利

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

高斯形状上下文描述子

冯祥卫,冯大政,侯瑞利

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

利用高斯窗函数,构建了一种新的形状上下文描述子,并将该描述子应用到形状配准当中.高斯形状上下文以参考点为中心建立一组高斯窗函数,根据中心点与其他采样点之间的欧氏距离,利用尽量多的采样点计算各个窗函数的值并组成形状描述子,描述点与点之间的位置关系.通过比较形状描述子之间的相似性,能够较为准确地找到两个形状间点与点的对应关系.实验表明,使用高斯形状上下文作为形状描述子,比传统的形状上下文能够更加准确地找到点与点的对应关系,使配准算法快速收敛,具有良好的抗噪性和鲁棒性.

形状上下文;高斯窗;形状描述子;形状配准;鲁棒性

形状是图像的重要特征.形状配准,特别是点配准在图像处理和模式识别领域得到了广泛的重视和发展.形状点配准主要通过迭代算法完成,分为两个步骤:①寻找两幅形状之间的点与点的对应关系;②根据对应关系计算变换.形状配准问题是一个非常复杂的非凸优化问题,存在多个局部极小点,因此,寻找一个好的初值,即找到准确的点与点的对应关系显得特别重要.为了解决这个问题,多种形状描述子被提出和深入研究[1].文献[2]提出了形状上下文(Shape Context,SC),并定义了形状上下文距离.形状上下文是一种基于轮廓的形状描述子,细致地描述了边缘点在形状中与其他的边缘点的空间位置关系.两个点之间的相似程度可以通过比较形状上下文距离来衡量.形状间的点与点匹配可以通过最小化形状上下文距离之和来实现.针对形状上下文的改进和应用成为了一个研究热点[3-5].但是,形状上下文采用的是硬分配的思想,图像中的每个点仅仅被分配到一个栅格中.在噪声、形变以及旋转的影响下,这种决策方式存在一定的缺陷.针对以上问题,笔者提出了高斯形状上下文(Gaussian Shape Context,GSC)描述子.高斯形状上下文首先以参考点为圆心按照一定分布规律建立一组高斯窗函数,根据高斯窗函数的中心点与其他采样点之间的欧氏距离,计算每个窗函数的值,再利用全部高斯窗函数的值组成该点的形状上下文描述子.高斯形状上下文描述子充分考虑到了形状作为整体的存在,利用全部采样点计算特征表示单元,融合了形状的局部细节信息和整体信息.与传统的形状上下文相比,这种算法不仅能够找到更为准确的点与点的对应关系,与配准算法较好地结合起来,而且在形变和噪声影响下有更好的鲁棒性.

1　形状上下文

形状上下文是一种基于轮廓的形状描述子[2],如图1所示.形状上下文首先对目标轮廓进行均匀采样,依次选取每个采样点作为参考点,以该参考点为中心建立极坐标系,并按照角度和距离划分栅格,统计落入每个栅格内的点数,构成该点的形状上下文描述子.令P和D分别代表原始形状和待配准形状的采样点集,选取di作为参考点,di∈D,利用该点与余下的Nd-1个采样点的相对位置关系构建特征向量.以点di为原心建立对数极坐标空间,将对数极坐标空间按照距离和角度划分为M×N个栅格.统计落入每个栅格内的点数,可以获得关于点di的特征直方图:

图1　形状上下文

其中,B表示栅格.直方图hi定义了点di处的形状上下文.任意选取目标形状上的某一点pj,pj∈P,令Cij=C(di,pj),表示点di和点pj的匹配距离,根据χ2检验统计,可得

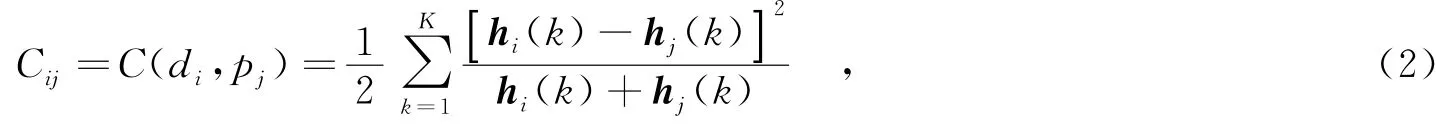
其中,Cij表示两个点之间的“相似度”,即形状上下文距离.通过比较形状上下文距离,可以确定形状间的点与点的对应关系.

2　基于高斯窗函数的形状上下文

2.1高斯形状上下文构建原理

形状特征描述子的构建需要尽量满足两个要求:一是尽可能多地保留有用信息,二是需要具备良好的抗噪性和鲁棒性.

(1)形状作为一个具有紧密的内在联系的整体,每个采样点之间都存在空间上和结构上的相互关系.因此,特征描述子的每个表示单元应当使用尽量多的采样点描述点与点之间的位置关系.形状上下文表示单元都为栅格,栅格仅仅描述了参考点与栅格所在区域的图像点的关联,而栅格内与栅格外的采样点之间的信息被忽略掉.文献[3]中提出的软形状上下文通过对栅格内的点进行离散权值加权并分配到周围的栅格中,虽然在一定程度上保留了这部分信息,但是软形状上下文构造过于简单,特别是在距离上只有一层,不能较为准确和全面地表示出这种相对关系.高斯形状上下文构建形状表示单元时,不再简单地将整体作为各个表示单元的叠加,而是全面地考虑各个单元之间的相对关系.

(2)形状上下文通过统计栅格内的点数来构建表示单元.根据式(1),形状上下文采用的硬分配的方式分配采样点,每个采样点仅仅只能被一个栅格统计,表示数值只能是整数,是一种离散的表示方式,而离散表示必然存在着阶跃变化.因此,当形状产生轻微的旋转或者形变的时候,形状上下文描述子可能会产生较为剧烈的变化,影响形状描述子的稳健性.这样的分配方式对于采样点在栅格的交界处分布较多的情况,目标产生微小形变,得到的形状上下文描述子却有很大的不同.如图1中所示,形状发生微小形变,位置由A点移动到B点,但是采样点分布的微小变化却引起形状上下文产生明显的变化.为解决这个问题,高斯形状上下文使用连续函数代替阶跃函数,用连续的或者近似连续的数值变化表示形状产生的变化,避免形状描述子出现剧烈变化,从而提升形状描述子的鲁棒性.

2.2构建高斯形状上下文表示单元

为了构建包含信息更为丰富、鲁棒性更强的形状表示单元,可以使用高斯窗函数作为特征表示单元对采样点的空间相对分布进行描述.传统的形状上下文采用的统计标准是二值化的、硬分配的,不具备各向同性;而高斯窗函数是连续的、平滑的、软决策的,且具备各向同性,从而对微小的形变具有较好的不变性.如图2所示,对杯子的边缘点进行采样得到的点为采样点,定义当前需要描述的采样点di为参考点.在二维图像中按照一定的分布规律选取坐标为(x,y)的点作为高斯窗函数的中心,定义该点为形状表示单元的中心点.该点相对于参考点di在某一坐标系下的距离为l,角度为θ,高斯窗函数的均值为零,标准差为σ,则高斯窗函数为

图2　高斯形状上下文

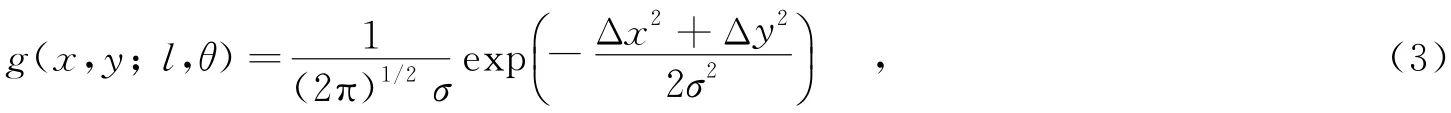
其中,Δx、Δy分别表示点到x、y的距离.形状上的某一采样点(i,i)对于该高斯窗函数的加权值为

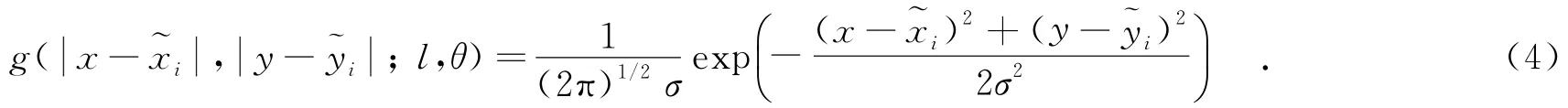
进一步,通过所有采样点可以得到以点(x,y)为中心的高斯窗函数的值为

从式(3)～(5)可以得出,使用高斯窗函数作为表示单元保留了距离和角度信息,即l和θ.新的表示单元根据采样点与中心点的欧氏距离,对全部的采样点加权计算得出窗函数值,并且距离中心点越近,对形状表示单元的影响就越大,这与实际情况相符合.由于高斯窗函数的各向同性,使用高斯窗函数作为形状表示单元在一定程度上也模糊了距离、角度变化以及非刚性形变.同时,针对传统形状上下文所采用的“栅格”会出现剧变的情况,高斯窗函数将形状的变化采取近似连续化数值表示,避免边缘点的微小挪动导致形状表示单元出现大的变化,提升了形状表示单元的鲁棒性.高斯窗的大小可以控制形状表示单元的模糊程度,选择大的高斯窗重点体现中心点在形状中的粗略位置信息,选择小的高斯窗则重点体现中心点附近的细节信息.

2.3构建高斯形状上下文描述子

单个的高斯窗函数形状表示单元可以描述所有采样点相对于中心点(x,y)的分布情况,多个有规律分布的高斯窗函数组成的形状上下文描述子就能比较全面和精确地描述参考点di在整个形状中的空间信息.如图2所示,高斯形状上下文以参考点di为原点建立极坐标系,并按照角度和距离划分平面空间,得到的交叉点作为高斯窗函数的中心点.在距离划分上,可以选择相同的半径,即R1=R2=R3,也可以选择依次增加的半径,即R1＜R2＜R3.在高斯窗函数的选择上,高斯窗的大小随着中心点与参考点的距离的增加而增加,从而使描述子对参考点附近的采样点分布变化更加敏感.在距离参考点较近的位置细致地刻画采样点的分布情况,注重体现结构上的细节变化;距离较远的采样点则用来粗略地描述参考点在形状中的空间位置,让更多的点产生更大的影响参与表示单元的构建,模糊容易受噪声影响的细微差别.同时,还可以根据迭代配准算法的配准情况调整高斯窗函数的大小.综上所述,并根据式(5)计算得到参考点di的M×N+1个高斯窗函数值组成特征描述子:

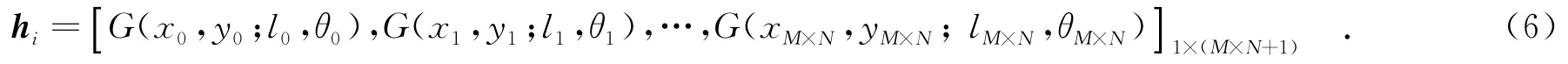
根据式(2)计算出形状之间点与点的形状上下文距离.

高斯形状上下文描述子是以参考点为中心,利用点与点之间的相对位置关系构建描述子,因此具备平移不变性.利用中心点与采样点之间欧氏距离矩阵的平均值,对坐标进行归一化以达到一定的尺度不变性.同时,由于高斯形状上下文表示单元可以模糊角度和距离差别,因此对轻微的旋转和不规则形变也具备一定的不变性.对于出现较大旋转的情况,可以将点的切线方向定义为零度角坐标轴.因此,高斯形状上下文描述子对参考点形成了由近及远,由细致到粗略,由点到局部到部分整体的描述,既提升了形状描述子的稳健性,又保证了精确性.值得注意的是,如果取足够多的高斯窗,本质上就对形状做了高斯平滑,滤除了形状中高频成分,而噪声往往存在于高频成分当中,因此,基于高斯窗函数的形状上下文描述子具有天然的鲁棒性.

3　配准算法

形状描述子构建完成以后,就需要通过按照一定的标准,比较点与点之间的“相似性”来找到最佳点与点的配准关系,然后根据得到的点与点对应关系计算配准变换.寻找准确的点与点对应关系和配准变换相互依赖,互为前提.找到准确的点与点的对应关系,对算法性能具有重要影响.寻找点与点的对应关系可以通过最小化代价函数实现[6],代价函数的统一形式为

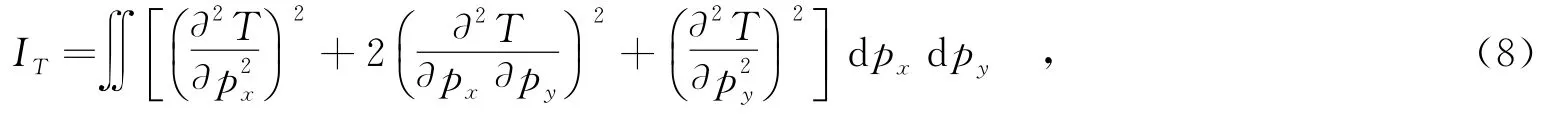
其中,λ为正则化参数.两个步骤相互迭代,互为前提,直到满足停止条件为止.薄板样条函数算法是一种非刚性变换,存在非线性计算,利用的信息比刚性变换要多,因此性能有一定的提升,但是计算较为复杂,计算复杂度为O(N3)[8].

4　仿真实验

为了验证笔者提出算法的有效性,进行了以下仿真实验.实验中所采用的计算机处理器为Intel i5-3570,主频为3.4 GHz,内存为4 GB,软件平台为MATLAB,版本为R2011b.实验中利用高斯形状上下文(GSC)和形状上下文(SC)方法构建形状描述子,使用匈牙利算法寻找点与点之间一对一的对应关系,利用薄板样条函数算法计算配准变换,分别记为GSC+TPS方法和SC+TPS方法.在实验中首先对配准形状和待配准形状进行编码,其中,对应点标记为相同的编号.进一步,定义配准率r为

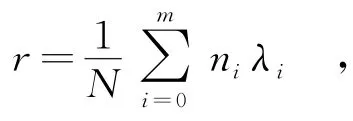
其中,N表示采样点数;i表示原始形状和待配准形状对应点的编码之差,该差不大于m则认为正确配准;ni表示配准图像和待配准图像的对应点的编码之差为i的数目;λi表示配准置信度,λi值越高,表示该点被正确配准的概率越高.在实验中,取m=2,λ0=1,λ1=0.8,λ2=0.6.配准算法采用薄板样条函数算法,因此,进一步定义目标形状和配准形状对应点之间的距离的平均误差为

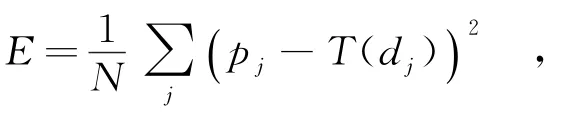
其中,E表示形状之间配准结果准确度.同时,根据式(8)计算变换所需要的弯曲能量IT.IT越大,表示配准形状需要做更为剧烈的形变才能完成配准要求.r、E和IT这3个量的大小和收敛速度共同实现对图像配准算法质量的考查.文中的实验采用文献[6]中所用的数据.为保证实验的公平性,两种方法的正则化参数λ的取值规则都是相同的,都以水平方向作为零度角.形状上下文角度方向等分为12组,距离方向分为5组,最终每个点的描述子为60维向量.高斯形状上下文在角度方向和距离方向,加上参考点的高斯窗,建立12× 5+1=61个高斯窗函数.高斯窗函数的标准差一般在0.25～0.35之间取值,如果形状较为紧凑,即点与点之间的平均距离小,则可以取相对较小的高斯窗;反之,则取相对较大的高斯窗.

实验1 采用的形状如图3(a)所示,待配准形状与原始形状之间存在明显的平移和非线性形变,没有添加噪声.每组实验迭代配准次数为8次.图3(b)与3(c)表示两种方法的最终配准结果,从图中可以看出, GSC+TPS方法的配准效果要优于SC+TPS方法.图4给出了两种方法的性能对比.从性能对比图4(a)可以发现,GSC+TPS方法较SC+TPS方法的首次配准率要高,GSC+TPS在首次配准时达到了74.40%,第2次配准中达到了88.00%,而SC+TPS首次配准的准确率为69.60%,收敛后配准率为78.80%,显示出GSC算法在构建形状描述子时具有良好的区分性.从图4(b)和4(c)中可以发现,GSC+TPS方法在平均误差和弯曲能量方面都要明显小于SC+TPS方法.在收敛速度上,GSC+TPS方法在第2次就达到收敛,而SC+TPS方法在第7次才收敛,GSC+TPS方法的收敛速度要明显快于SC+TPS方法.在使用匈牙利算法和薄板样条函数算法中,都存在计算复杂度为O(N3)的操作,因此,GSC+TPS方法能够快速收敛的性质大大加快了形状的配准速度,在处理大规模问题,例如识别问题中,具有较大的优势.该实验证明了GSC+ TPS方法在形状产生非线性形变下的有效性.

图3　SC+TPS与GSC+TPS方法配准图

图4　性能对比图

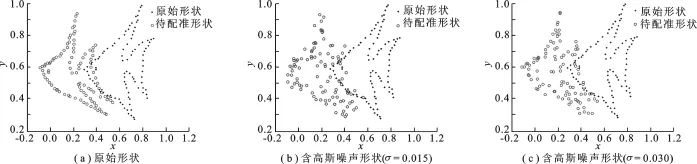
图5　配准形状

实验2 考查形状边缘受到高斯噪声污染的情况下两种方法的性能.实验中高斯噪声的均值为零,标准差从0.005到0.050,共10组,每组标准差增加0.005,最大迭代次数为100,每组做300次重复试验.实验中所采取的原始形状和部分添加噪声的形状如图5所示.随着噪声的增加,待配准图像产生的变化越来越剧烈,因此寻找对应点,实现配准难度也越来越高.以标准差σ=0.015为例,GSC+TPS方法在配准率、弯曲能量、平均误差方面均要优于SC+TPS方法.同时,GSC+TPS方法平均只需要3次左右的迭代就达到了收敛,而SC+TPS甚至在除去不收敛的情况下,平均需要8次左右的迭代才能收敛.GSC+TPS方法在噪声下仍可以快速收敛的性质对于处理容易受噪声污染的自然图像时,可以较大地节约计算量.表1给出了GSC+TPS方法和SC+TPS方法的配准率、弯曲能量和平均误差.从表中可以看出,特别是在噪声标准差为0.005～0.030时,GSC+TPS方法在各项中性能标准中不仅明显高于SC+TPS方法,而且各项参数的波动幅度也较小,说明GSC+TPS方法具有较好的抗噪性和鲁棒性.随着噪声标准差增加到0.045,GSC+ TPS方法的性能只是略优于SC+TPS方法,这是因为过大的噪声有可能破坏形状的结构信息,此时进行配准的意义已经不大.该实验证明了GSC+TPS方法在噪声情况下的有效性.

表1　SC+TPS与GSC+TPS在高斯噪声情况下的配准性能

5　结束语

笔者提出了一种基于高斯窗函数的形状上下文描述子,高斯形状上下文利用一组高斯窗函数建立栅格,构建性能稳健的形状描述子,在形变和噪声情况下能够寻找到更为准确的点对点对应关系,并且能够与迭代最近点(Iterative Closest Point,ICP)、薄板样条函数等计算变换方法结合起来实现图像的配准任务,具有更高的配准准确率和更快的收敛速度,性能也更为稳健.

[1]ZHANG D,LU G.Review of Shape Representation and Description Techniques[J].Pattern Recognition,2004,37(1): 1-19.

[2]BELONGIE S,MALIK J,PUZICHA J.Shape Matching and Object Recognition Using Shape Contexts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(4):509-522.

[3]LIU D,CHEN T.Soft Shape Context for Iterative Closest Point Registration[C]//Proceedings of the IEEE International Conference on Image Proceedings:2.Piscataway:IEEE,2004:1081-1084.

[4]SU Y.Spectra of Shape Contexts:an Application to Symbol Recognition[J].Pattern Recognition,2014,47(5): 1891-1903.

[5]PREMACHANDRAN V,KAKARALA R.Perceptually Motivated Shape Context Which Uses Shape Interiors[J]. Pattern Recognition,2013,46(8):2092-2102.

[6]CHUI H,RANGARAJAN A.A New Point Matching Algorithm for Non-rigid Registration[J].Computer Vision and Image Understanding,2003,89(2):114-141.

[7]KUHN H W.The Hungarian Method for the Assignment Problem[J].Naval Research Logistics Quarterly,1955,2(1/ 2):83-97.

[8]BOOKSTEIN F L.Principal Warps:Thin-plate Splines and the Decomposition of Deformations[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(6):567-585.

(编辑:郭 华)

Gaussian shape context descriptors

FENG Xiangwei,FENG Dazheng,HOU Ruili
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

The shape context(SC)descriptors based on the Gaussian window(GSC)are proposed.The GSC descriptors can be used to match shapes.Encircling the reference point,the GSC sets up a group of Gaussian window functions.According to the Euclidean distance between the center points and the sampling points,the GSC describes the spatial relations between sampling points based on the shape descriptors calculated by Gaussian window functions by the use of as many sampling points as possible.More accurate correspondences between two shapes are determined by comparing the similarities of the shape descriptors. Experimental results show that the GSC can find more accurate correspondence relations and provide a good initial value.The proposed descriptors can also make the matching algorithm converge fast,while keeping a good anti-noise and robust performance compared with SC.

shape context;Gaussian window;shape descriptors;shape matching;robust

TP391

A

1001-2400(2016)04-0045-06

10.3969/j.issn.1001-2400.2016.04.009

2015-05-14 网络出版时间：2015-10-21

国家自然科学基金资助项目(61271293)

冯祥卫(1990-),男,西安电子科技大学博士研究生,E-mail:sdfengxw@126.com.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.018.html