考虑流变特性的隧道围岩变形效应分析

王 强

(中铁十一局集团第二工程有限公司，湖北十堰 442000)



考虑流变特性的隧道围岩变形效应分析

王 强

(中铁十一局集团第二工程有限公司，湖北十堰 442000)

为了探讨考虑流变效应情况下隧道围岩和衬砌的变形情况，从而进一步确定隧道的合理衬砌时机。首先，分析围岩的流变特性对隧道变形和衬砌抗力的影响，通过理论推导得到了同时考虑黏弹塑性的隧道围岩变形计算公式，该公式包含时间参数，可确定达到不同衬砌位移及围岩位移所需要的时间。然后，以南龙铁路隧道工程为背景，针对隧道拱顶下沉、周边收敛、围岩压力和初衬内力，开展隧道二衬合理支护时机的监测分析，得到围岩变形计算公式中的待定系数，并确定隧道衬砌的合理支护时机。将得到的结果与现场监测的结果进行对比，发现二者得到的二衬支护时机基本相同，从而验证计算结果的正确性。

隧道；流变；衬砌；围岩

随着我国铁路隧道建设事业的发展，新奥法建设山岭隧道的理念已经越来越被隧道设计和施工技术人员所接受。新奥法强调通过现场动态监控及时反馈围岩情况，确定衬砌加固时机，达到动态及时支护的效果。及时支护的优点在于能充分发挥围岩的自身承载能力，防止围岩由于支护过晚而产生的松脱压力，增加二次衬砌的负荷，甚至发生塌方等安全施工引起隧道破坏。可见，为了有效发挥围岩自身承载能力确保隧道的稳定性，需对二次衬砌的合理加固时机进行确定。许多学者进行了相应研究[1-5]，如辛全山等[3]利用二次耦合加固理论和现场监测结果，提出监测结果的变形转折点即为二衬加固的合理时间；荣耀[2]根据岩体应变能释放时间，给出了二衬的大致时间；张鹏等[4]利用芬纳公式和圆孔扩张理论，根据变形监测结果确定二次衬砌的合理加固时机。尽管以上这些研究给出了二衬衬砌加固时机的确定方法，但未考虑岩体的流变性，而岩体的流变特性是其重要的力学性质，隧道的变形可以认为是岩体流变特性参数和围岩应力状态的函数[6-9]，并且岩体的流变控制着工程的变形和问题，对围岩的应力状态有着强烈的影响[10]。

本文以南龙铁路隧道开挖和支护为工程背景，围岩较为破碎，存在一断层，围岩级别为Ⅴ级，围岩的流变现象较为明显，此时若仅采用传统的弹塑性分析方法，则无法反映由于围岩流变特性而导致的围岩和衬砌的变形。因此，本文探讨了考虑流变效应情况下，隧道围岩和衬砌的变形情况，并将结果与监测的结果进行对比，以验证计算结果的正确性。

1 工程概况与监测分析

1.1 工程概况

以南龙铁路隧道为工程背景，隧道围岩主要由砂岩和白云质灰岩组成，岩石较为破碎，存在一断层，围岩级别为Ⅴ级。该隧道采用复合式衬砌，初期支护为锚喷支护，二衬为模注混凝土曲墙式，横断面如图1所示，隧道支护结构参数见表1。

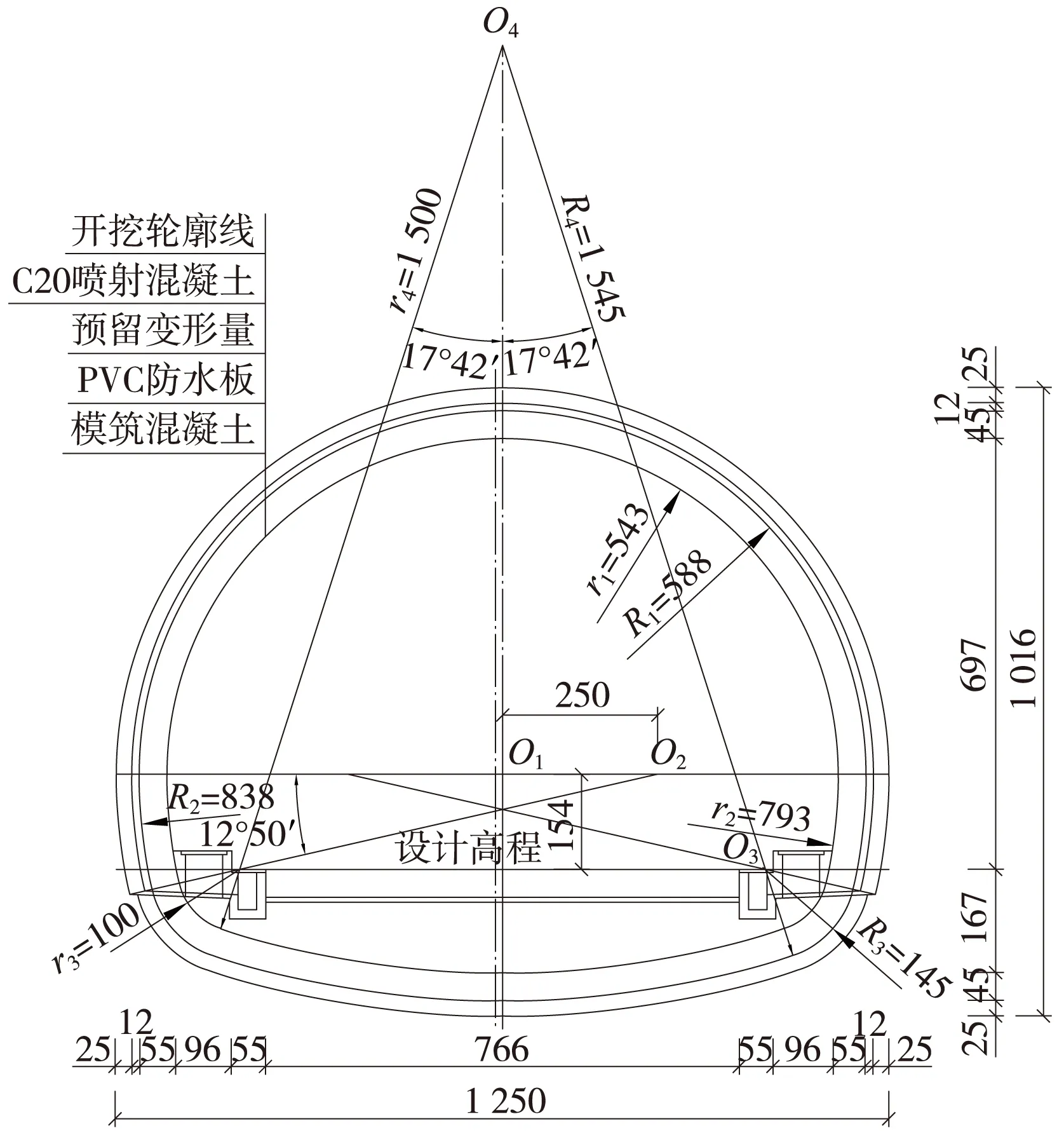
图1 隧道横断面(单位：cm)

名称弹模/GPa重度/(kN·m-3)截面积/mm2惯性矩/m4系统锚杆210.077.6380-初衬24.822.61000-二衬28.324.530000.00223

1.2 监测结果与分析

选取隧道的拱顶、拱腰等位置作为特征点(图2)，分析相应的围岩和支护结构的内力和变形。

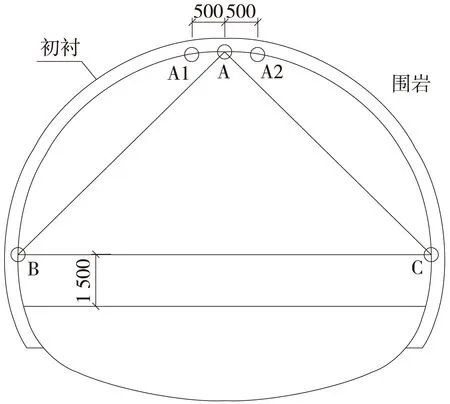
图2 围岩隧道变形监测测点布置(单位：mm)

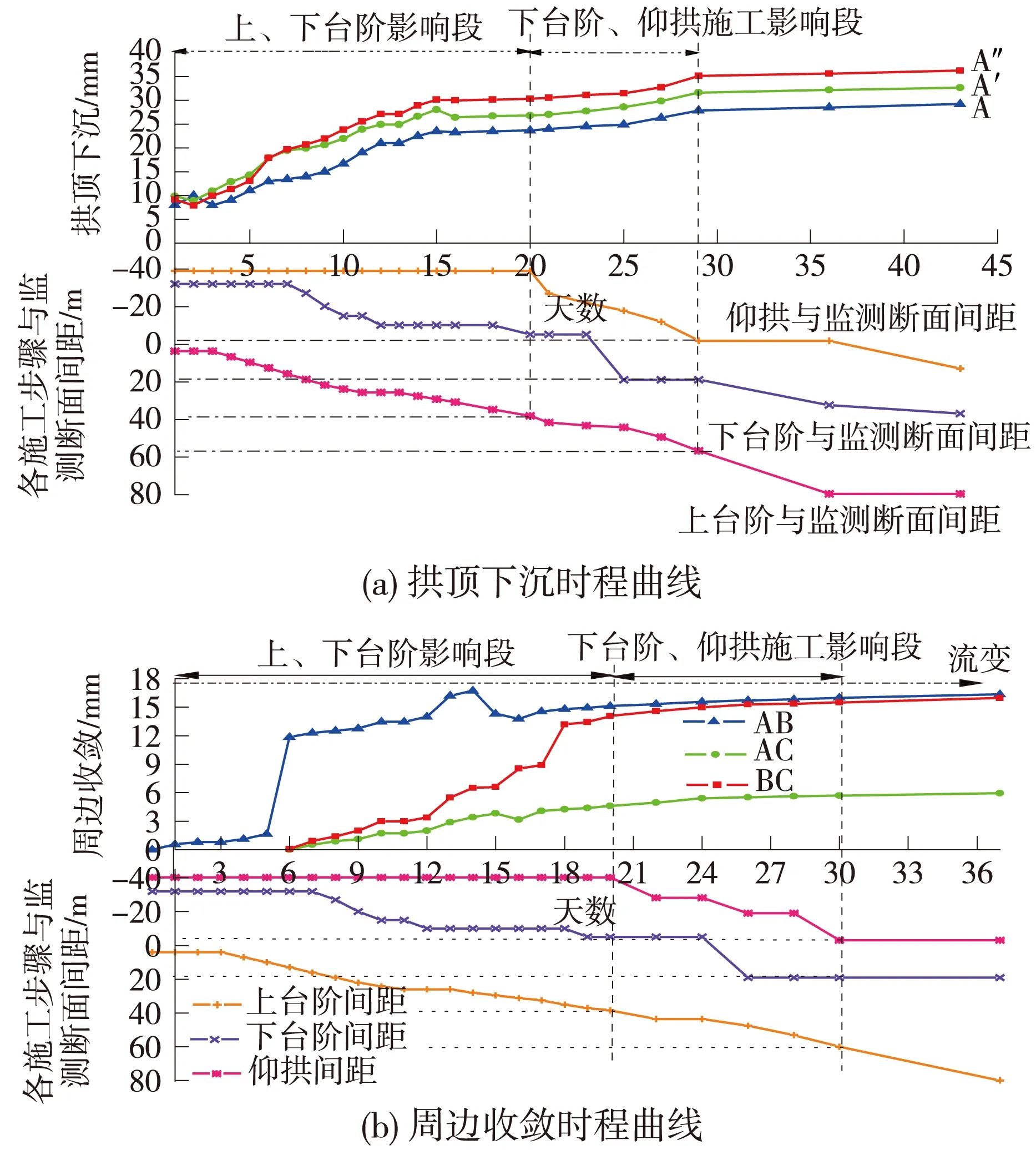
图3 隧道监测时程曲线

图3为隧道断面监测项目时程图，从图3(a)看出，拱顶下沉在开始阶段受上下台阶开挖的影响较为显著，这一阶段所形成的下沉量占总下沉量也较大，在开挖后第15 d左右，上下台阶开挖的影响逐渐变小，如图3(a)中15～20 d的曲线斜率明显减小，在第20 d，下台阶开挖到监测断面所在位置，拱顶下沉曲线明显出现反弯，到第28 d时，各开挖步骤的影响已趋于零。从图中还可以看出，当拱顶下沉平稳时，掌子面距离监测断面约60 m，下台阶距离监测断面约20 m，而仰拱的开挖对拱顶下沉的影响较小。由于开始阶段埋设测点被破坏，导致图3(b)中AC、BC测线前几天没有读数，但是从AB测线可以看出，前期下台阶和仰拱开挖皆处于停滞阶段时，AB线的收敛值发展较快，占到总收敛值的60%左右，因而上台阶开挖对于周边收敛的影响非常显著。第9 d后下台阶开始施工，3条测线周边收敛量都有大幅度提高，但是从后面19～30 d的曲线可见下台阶和仰拱开挖对于周边收敛影响较之上台阶要小的多。周边收敛达到平稳时掌子面距离监测断面约60 m，下台阶距离监测断面约20 m，所有这些都和拱顶下沉显现出同样的规律。

从表2可见，在Ⅴ级围岩中开挖隧道，周边位移收敛和拱顶下沉稳定时间约为30d。根据欧阳建等[11]，张周平等[10]的建议，由于Ⅴ级围岩稳定性极差，周边位移收敛和拱顶下沉稳定时间可取上限值，即24 d。另外，周边位移收敛和拱顶下沉达到稳定后，监测断面与掌子面之间的平均距离为67 m，同样可取上限值102 m。从围岩压力和初衬内力检测结果看，围岩和支护结构应力达到平衡所需时间及与掌子面间距都稍大于变形监测结果，能与变形监测结果形成映衬。

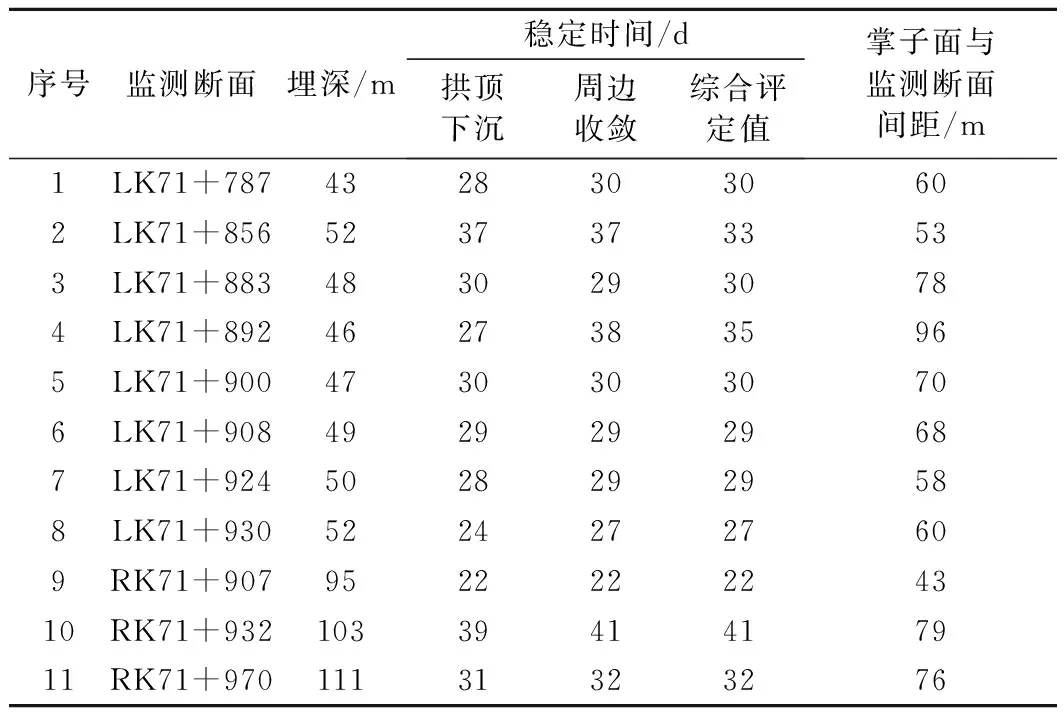
表2 隧道变形稳定时间

2 隧道二衬时机的确定

图4为考虑弹塑性变形情况下，圆形隧道的塑性区半径与围岩压力、衬砌支护效果之间的关系[12,13]，可得到衬砌抗力的计算公式为

(1)

式中，R0为围岩的塑性区半径；r0为隧道的开挖半径；q为隧道的围岩压力；P0为衬砌的支护抗力；c为围岩的黏结力；φ为围岩的内摩擦角。

图4 圆形隧道的塑性区半径

假设岩体符合Mohr-Coulomb准则，根据隧道的边界条件和变形协调方程，根据弹塑性力学方法[14]可得到衬砌和围岩的位移计算公式

(2)

式中，r0≤r≤R0。

(3)

式中，r1≤r≤r0；up为塑性区的位移；ucp为衬砌的位移；r为计算参考位置的半径；r1为初衬的内半径。

当考虑隧道围岩的流变特性时，其衬砌的抗力、位移和围岩的位移可通过下式得到

(4)

(5)

(6)

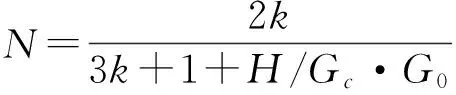
k=3-4μ；kc=3-4μc

通过进一步整理，可将式(6)变换为

(7)

当r=r1时，则式(7)表示衬砌临空面位移，即

(8)

其中，r0、r1分别为设计开挖轮廓半径和衬砌内半径。

N、fc0可以通过隧道开挖轮廓的半径r0、初衬的内半径r1和衬砌泊松比μc计算确定；G0、μc可通过相关试验和勘察报告得到。为了确定隧道围岩的变形情况，需进一步确定G∞、a和R0，其中G∞和a可通过岩石的流变特性试验得到，R0可利用隧道围岩现场监测结果得到。若未能进行岩石的流变试验，可通过现场变形监测，拟合得到G∞、a和R0。此外，式(8)仅适用于隧道断面为圆形的情况，而本文的隧道断面为城门洞形，因此，本文根据隧道断面的等效变换方法[15]，将城门洞形隧道断面转换为圆形隧道断面，则对应的等效半径为

(9)

式中，r为外接圆的半径；h为隧道断面的高度；B为隧道跨度的1/2。

通过式(9)的等效变换方法，可得到相应隧道和衬砌的等效半径，如表3所示。

表3 隧道和衬砌的等效半径 m

通过式(8)拟合表2中不同断面的拱顶下沉曲线，可得G∞=6 115 036；R0=9.6；a=0.076 4。从而得到围岩流变情况下，隧道拱顶下沉的计算公式为

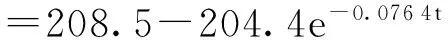
(10)

图5为Ⅴ级围岩拱顶下沉理论计算值与实测值的对比结果，可见，考虑围岩流变特性的拱顶下沉理论计算曲线与现场实测的结果具有相同的发展趋势。当t→∞时，可得到隧道拱顶的最终沉降量为208.5 mm，从理论计算曲线中得到，当拱顶沉降达到总沉降量80%所需的时间为20 d，即隧道的二衬支护时机为≥20 d，该结果与监测得到的结果相同，从而说明计算结果的正确性。

图5 Ⅴ级围岩拱顶下沉理论计算值与实测值

3 结论

(1)探讨了围岩的流变特性对隧道变形和衬砌抗力的影响，通过理论推导得到了同时考虑黏弹塑性的隧道围岩变形计算公式，该公式包含了时间参数，可确定达到不同衬砌位移及围岩位移所需要的时间。

(2)以南龙铁路隧道工程为背景，针对隧道拱顶下沉、周边收敛、围岩压力和初衬内力，开展了隧道二衬合理支护时机的监测分析，得到了围岩变形计算公式中的待定系数，并确定隧道衬砌的合理支护时机。将得到的结果与现场监测的结果进行了对比，发现二者得到的二衬支护时机基本相同，从而验证了本文计算结果的正确性。

[1] 张社荣,梁礼绘.考虑三维应力旋转的隧洞衬砌支护时机研究[J].水利学报,2007,38(6):704-709.

[2] 荣耀.巷道支护时机与围岩级别关系的研究[J].矿山压力与顶板管理,2003,20(4):11-13.

[3] 辛全山,刘善永,赵延峰.利用二次耦合理论确定二次支护的最佳时间[J].山东煤炭科技,2003(4):16-17.

[4] 张鹏,李宁,何敏.软岩圆形隧洞衬砌支护时机现场变形监测判据研究[J].西安理工大学学报,2007,23(2):140-143.

[5] 莫阳春.隧道底部隐伏空腔充水对二次衬砌内力影响研究[J].水文地质工程地质,2011,38(5):31-37.

[6] Jiang Z, Liang J. Analysis method of influence on longitudinal deformation of tunnel heaving due to excavation[J]. Electronic Journal of Geotechnical Engineering, 2013,18:5473-5480.

[7] 赵晓勇.TBM法隧道施工下穿涵洞的数值模拟研究[J].地下空间与工程学报,2011,7(3):513-517.

[8] 张凯,巨能攀,霍宇翔,等.岩溶隧道围岩动态分级方法研究[J].中国地质灾害与防治学报,2012,23(1):67-71.

[9] 周毅,邓辉,徐静.叙(永)大(村)铁路某高压充水溶洞隧道安全厚度数值模拟[J].中国地质灾害与防治学报,2012,23(3):82-85.

[10]张周平,余伟健,高谦,等.金川深部工程围岩支护时机与参数设计研究[J].金属矿山,2008(2):40-44.

[11]欧阳建,付云升,石维新,等.南水北调中线西四环暗挖段暗涵二衬支护时机的研究[J].南水北调与水利科技,2008,6(1):48-51.

[12]王祥秋,杨林德,高文华.软弱围岩蠕变损伤机理及合理支护时间的反演分析[J].岩石力学与工程学报,2004,23(5):793-796.

[13]Shalabi F I. FE analysis of time-dependent behavior of tunneling in squeezing ground using two different creep models[J]. Tunnelling and Underground Space Technology, 2005,20(3):271-279.

[14]周德培.流变力学原理及其在土木工程中的应用[M].成都:西南交通大学出版社,1995.

[15]傅鹤林.隧道衬砌荷载计算理论及岩溶处治技术[M].长沙: 中南大学出版社,2005.

Deformation Analysis of Surrounding Rock Mass of Tunnel under Rheological Effect

WANG Qiang

(No.2 Engineering Co.， Ltd. of CR11BG， Shiyan 610031， China)

To study the deformation of surrounding rock mass and lining of tunnel under rheological effect and further determine proper lining time， the effect of rock rheological characteristic on the deformation and lining anti-force is analyzed， and the calculation formula of the deformation of tunnel surrounding rock mass is deduced with the analytical method. The formula consists of time factor to calculate the time needed to reach the certain value of lining resistant pressure， displacement and surrounding rock mass displacement. In view of the tunnel vault sink， the peripheral convergence， the pressure of surrounding rock and the internal force， the reasonable support time for second lining is monitored and analyzed to determine the specific coefficient of surrounding rock deformation formula， and ultimately determine the reasonable support time for tunnel lining. The results are compared with that from site monitoring and the support times of the two are much the same， which validates the correctness of the proposed calculation method．

tunnel; rheological characteristic; lining; surrounding rock mass

2016-04-19；

2016-05-15

王 强(1976—)，男，高级工程师，2000年毕业于石家庄铁道学院土木工程专业。

1004-2954(2016)11-0100-04

U451+.2

A

10.13238/j.issn.1004-2954.2016.11.022