困难山区铁路主要技术标准与工程投资关系研究

郭 靖，李远富

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)



困难山区铁路主要技术标准与工程投资关系研究

郭 靖，李远富

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

铁路主要技术标准与工程投资有着十分密切的关系，通过深入探讨铁路主要技术标准，从统计学的角度研究铁路主要技术标准与工程投资的关系，建立工程投资关于铁路主要技术标准的多元非线性回归模型。并结合实际算例说明回归模型的良好的拟合度，研究各项主要技术标准之间的相关性，分析各项主要技术标准对工程投资的影响趋势与影响程度，从而在实际的应用中能够有的放矢地关注关键的技术标准以及科学合理地决策出各项主要技术标准，以达到优化线路设计、节约工程投资的目的。

山区铁路；技术标准；工程投资；非线性回归分析

在铁路选线设计中，线路选线的质量将直接关系到铁路工程建设的可靠性、安全性、技术可行性和经济合理性及社会接纳性，关系到铁路和地方经济社会的发展，因而它是高速铁路建设应重视的首要问题[1]。其中，在铁路预可行性研究阶段，主要技术标准的选择是一项十分重要的决策，决策的科学合理与否将直接关系到线路施工的难易程度、工程投资[2]。王柢教授认为成昆铁路本可以决策出更加科学合理的技术标准，他认为由于选择了不合理的技术标准，线路的施工遭遇比较大困难，工程投资消耗较大[3]。因此，为了选择科学合理的主要技术标准，为了综合优化线路的设计，减少工程投资，研究铁路主要技术标准与工程投资的关系是十分必要的，对于西南的困难山区，尤其如此。

铁路主要技术标准对于铁路的工程投资均具有重大影响，那么，在具备足够多的设计资料的条件下，便可以从统计学的角度，寻找出铁路工程投资与铁路主要技术标准之间的关系，建立它们之间的数学模型。并且尝试分析各项主要技术标准之间的密切程度以及分析各项主要技术标准对工程投资的影响趋势与影响程度，从而达到在以后的设计中指导铁路主要技术标准的决策、尽量节约工程投资的目的。本文拟就采用统计学的多元非线性回归分析方法，研究困难山区快速铁路主要技术标准与建设期的土建工程投资的关系。

1 工程投资的计算

由于地形对工程投资影响很大，不同的地形下选用相同的技术标准需要的工程投资差异很大，因此在进行工程投资的计算与预测之前，首先应对地形进行分类。在铁路选线设计中，一般采用聚类分析和判别分析对地形进行分析[4]。地形分类前人已有较为完善的研究，在此不进行详细界定。

在研究铁路主要技术标准与工程投资的关系时，工程投资的计算主要是基于既有线路的统计数据。对于已经设计施工完成的线路，统计线路的土建工程投资，包括路基工程、桥涵工程、隧道工程、轨道工程、通信及信号工程、拆迁工程、房屋、其他运营生产设备及建筑物、其他间接费等各项费用[5]，即可得到在一定的技术标准条件下的工程投资。在实际的统计计算当中，由于工程项目种类繁多，计算复杂，可以通过统计路基、桥梁、隧道占总的工程投资的比重，再分别统计路基、桥梁、隧道的工程数量，也可以得到总的工程投资。可通过下列数学公式计算工程投资[6]

式中，Y为工程投资；m1、m2、m3分别为路基、桥梁、隧道每正线km的工程数量；p1、p2、p3分别为路基、桥梁、隧道工程单价；β为路基、桥梁、隧道工程投资占总的工程投资的比重。

2 铁路主要技术标准的选择

铁路主要技术标准包括正线数目、牵引种类、机车类型、牵引质量、限制坡度、最小曲线半径、机车交路、到发线有效长度和闭塞类型[7]。但是像铁路等级、速度目标值、站间距离等项指标仍然可以说是铁路的主要技术标准，因为其对铁路工程的设计、施工、建设、运营具有重要影响。各项铁路主要技术标准对于工程投资虽均有较大影响，但仍有轻重之分。在实际的工程实践中，限制坡度、最小曲线半径、到发线有效长度、站间距离对工程投资具有非常重大的影响，因此，本文拟选择限制坡度、最小曲线半径、到发线有效长度、站间距离等4项铁路主要技术标准，深入分析研究4项主要技术标准与工程投资之间的关系。

3 工程投资的多元非线性回归数学模型

现有的工程投资数学模型建立的思想，主要是在已知路基、桥梁、隧道占总的工程投资的比重的情况下，分别统计路基、桥梁、隧道的工程数量，再分别回归出路基、桥梁、隧道的工程数量及工程投资关于铁路主要技术标准的数学模型，最后3项工程的数学模型相加即可得总的工程投资数学模型，这一点上文已经简单提及过。

为了提高效率，尝试直接采用回归分析方法建立工程投资关于主要技术标准的数学模型。在得到拟合显著的多元非线性回归数学模型之前，首先尝试了多元线性回归，但是结果不甚理想，因而选择了更为合理的多元非线性回归模型。通过进行多元非线性回归分析，首先得到了拟合最为显著的工程投资数学模型[8]

(1)

式中，Y为工程投资；R为最小曲线半径；G为限制坡度；S为站间距离；Lyx为到发线有效长度；a0～a9为未知系数。

模型(1)较为复杂，通过多种组合计算分析，可以将模型(1)化简为如下模型(2)，模型(2)较模型(1)具有一定的简便性，但准确性有所降低

(2)

式中，各参数含义同上。

模型(2)仍然可以继续化简，但要损失较大的准确性。可将模型(2)继续化简成如下模型

(3)

式中，各参数含义同上。

为了分析验证以上3个工程投资的多元非线性回归数学模型，将结合实际算例分析其精度，比较分析各项主要技术标准对工程投资的影响趋势与影响程度，分析各项技术标准之间的密切程度。

4 工程投资数学模型实例分析

4.1 工程投资数学模型的分析验证

实例选取了处在西南困难山区的兰渝快速铁路17组工程投资数据[6]及其对应的各项主要技术标准，通过多元非线性回归分析计算得出了3个模型的各项系数及拟合度[9]。模型各项参数值分别见表1、表2及表3。模型拟合度见表4。

从表4可以看出，模型(1)与模型(2)的拟合度都比较高，模型(1)的拟合度达到了0.542，模型(2)的拟合度达到了0.461，而模型(3)的拟合度只有0.263，这说明各组数值与前两个工程投资的回归方程拟合很好，回归结果显著，能很好地表达出了各项铁路主要技术标准与工程投资之间的关系，只是在精度上略有差别。在实际的工程实践应用当中，可以根据所需要的计算与预测精度来合理地选择工程投资模型。

表1 模型(1)各项参数估计值

表2 模型(2)各项参数估计值

表3 模型(3)各项参数估计值

表4 模型拟合度

通过模型(1)预测出工程投资，并与实际的工程投资进行对比，并计算误差，见表5。

表5 实际工程投资与预测值误差分析

通过绘制困难山区17组工程投资的实际值与多元非线性回归模型(1)的预测值的对比图(图1)，可以很直观地看出模型(1)对实际值具有良好的拟合。

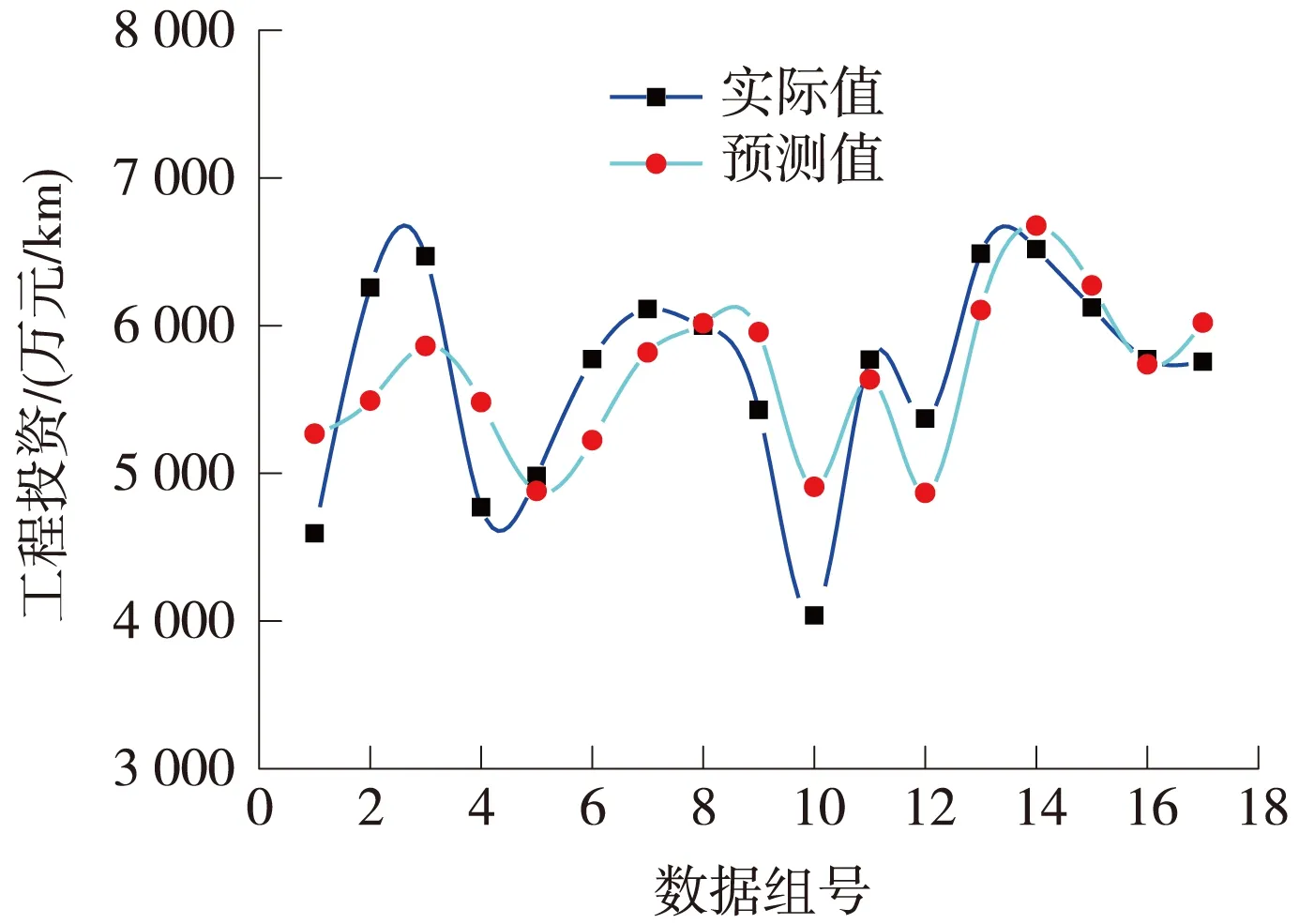
图1 工程投资的实际值与多元非线性 回归模型(1)的预测值的对比

通过以上分析，采用多元非线性回归分析所得到的工程投资数学模型，能很好地拟合实际的工程投资，从而很好地表现了困难山区铁路主要技术标准与工程投资的关系， 是能够用于实际的工程实践当中的。

4.2 铁路主要技术标准之间的相关性分析

铁路主要技术标准之间如果存在较强的相关性，会导致严重的多重共线性问题，从而影响回归系数估计值的准确性，最终导致不能正确判断各项技术标准对工程投资的影响程度，甚至无法解释工程投资预测值的意义[10]。因此，在分析各项技术标准对工程投资的影响趋势与影响程度之前，有必要先分析各项技术标准之间的相关性。

为了诊断铁路主要技术标准之间是否存在多重共线性的问题，可以采用相关系数法。相关系数能够反映变量之间关系的密切程度，以及是正相关还是负相关，是一种简单又实用的因素分析方法，皮尔逊相关系数计算公式[10]为

(4)

分别计算每两项技术标准的相关系数，得出了相关系数矩阵，计算结果见表6。

表6 各项技术标准之间的相关系数矩阵

4.3 铁路主要技术标准对工程投资的影响趋势与强度分析

工程投资的非线性回归数学模型能够对工程投资进行预测，但是不能用于分析各项铁路主要技术标准对工程投资的影响程度与影响趋势，因为工程投资的数学模型是各项铁路主要技术标准对工程投资共同影响的结果，是数量上的函数关系。况且，各项技术标准并不是完全独立的，它们之间或多或少地存在一定的交互作用，并不能完全地表示出各项技术标准对工程投资的影响关系。如果只是用检验的方法，通过判定回归系数来分析各项技术标准对工程投资的影响，那么很可能会得出完全错误的结论。

为了分析出各项铁路主要技术标准对工程投资的影响程度与影响趋势，同样的可以采用相关系数法，其计算方法如上文述及的公式(4)。分别计算各项铁路主要技术标准与工程投资的皮尔逊相关系数，见表7。

表7 各项技术标准与工程投资皮尔逊相关系数

5 结论

(1)利用多元非线性回归分析建立的工程投资关于铁路主要技术标准的数学模型具有较高的拟合度。在预可行性研究阶段，工程投资与铁路主要技术标准之间的关系近似地可以用数学函数关系直接表达。

(2)工程投资关于铁路主要技术标准的数学模型预测出的工程投资与实际工程投资之间误差在可以接受的范围，基本在10%以内，这表明在铁路预可行性研究阶段，用该模型预测铁路土建工程投资具有一定参考意义。

(3)在满足实际工程实践需要精度的情况下，可以将工程投资数学模型进行适当地简化，有助于提高计算效率，但要损失一定的精度。

(4)铁路主要技术标准之间的相关系数较小，说明从统计学的角度来说并没有显著的相关性，是可以同时得到最佳匹配的技术标准的。在科学合理地决策铁路主要技术标准时，应当贯彻综合优化的思想，以系统工程理论与优化技术为手段，决策出最佳匹配的技术标准。

(5)铁路主要技术标准对于工程投资有很大影响。其中限制坡度对工程投资影响最大且与工程投资呈现负相关关系；其次为最小曲线半径，其与工程投资呈现正相关关系。因此在实际的工程实践中，应该高度重视限制坡度与最小曲线半径的选择，慎用最小曲线半径。

[1] 朱颖.铁路选线理念的创新与实践[J].铁道工程学报，2009(6)：1-5.

[2] 李益群.铁路工程预可行性研究合理确定工程投资的方法[J].铁道标准设计，2011(5):116-118.

[3] 王柢，王大寿.工程决策中的综合优化——以铁路为例[M].成都：西南交通大学出版社，2002.

[4] 李敏.铁路主要技术标准和计算速度综合优化[D].成都：西南交通大学，1990.

[5] 李远富.线路勘测设计[M].北京：高等教育出版社，2004.

[6] 程永跃.兰渝铁路主要技术标准的综合优化研究[D].成都：西南交通大学，2008.

[7] 中华人民共和国住房和城乡建设部.GB50090—2006铁路线路设计规范[S].北京：中国计划出版社，2006.

[8] 后宗彪.费用现值目标函数铁路主要技术标准综合优化[D].成都：西南交通大学，2006.

[9] 朱星宇，陈勇强.SPSS多元统计分析方法及应用[M].北京：清华大学出版社，2011.

[10]马立平. 回归分析[M].北京：机械工业出版社，2014.

[11]王彦华.兰州至重庆铁路限制坡度的研究[J].铁道勘察，2006(2):45-48.

Research on Relationship between Main Technical Standards and Project Investment for Difficult Mountain Railways

GUO Jing， LI Yuan-fu

(MOE Key Laboratory of High-speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031, China)

The main railway technical standards correlate closely with project investment. Based on intensive discussion on main technical standards and the researches on the relationship between main technical standards and project investment for difficult mountain railways in perspective of statistics， the nonlinear regression model of project investment related to the main technical standards is established. With reference to practical examples， the good fit of regression model is illustrated， and the correlation between the main technical standards is studied， and the influence trend and influence degree of the main technical standards on the project investment are analyzed to allow attention to be focused on key technical standards in practical application and to define scientific and rational technical standards for the purpose of optimizing location design and saving project investment．

Mountain area railways; Technical standards; Project investment; Nonlinear regression analysis

2016-03-15；

2016-04-26

郭 靖(1991—)，男，硕士研究生，2014年毕业于西南交通大学土木工程专业，工学学士，E-mail：513390372@qq.com。

1004-2954(2016)11-0037-04

U212

A

10.13238/j.issn.1004-2954.2016.11.010