岩样微裂隙分布与单轴压缩破坏关系模拟研究∗

何耀宇宋选民邢平伟

(1.太原理工大学采矿工艺研究所,山西省太原市,030024; 2.太原理工大学继续教育学院,山西省太原市,030024)

岩样微裂隙分布与单轴压缩破坏关系模拟研究∗

何耀宇1宋选民1邢平伟2

(1.太原理工大学采矿工艺研究所,山西省太原市,030024; 2.太原理工大学继续教育学院,山西省太原市,030024)

采用有限元数值模拟的方法,对不同裂隙分布的岩石试样进行单轴加载压缩的数值模拟试验,通过引入压剪指数和拉伸指数对岩样的破坏进行判断,分析不同裂隙条件下岩样的破坏特征及其倾向程度,探索裂隙岩样的破坏机理和影响规律。研究结果表明单轴压缩条件下,标准的裂隙岩样破坏主要受拉应力控制,且破裂面出现的概率具有单斜破坏面＞竖向破坏面＞锥形破坏面的特征,其结论与实验室的大量试验结果吻合,并从机理上解释了微裂隙岩石单轴压缩破坏过程。

岩样破坏 岩样微裂隙 裂隙形态 单轴压缩 破坏指数 数值计算

随着深部开采矿区的增多,地下岩石工程稳定性的问题日渐突出。对于矿业工程领域而言,解决地下岩石工程稳定性的基础是岩石力学,岩石力学理论的不断进步才会带来岩石工程稳定性分析的飞跃。地下岩石作为一种经历多次地质构造运动时期作用并留有构造形迹的复杂天然材料,其内部存在着大量的弱面及微裂隙,岩石的破坏通常是沿着弱面滑动的压剪破坏和弱面分离的张拉破坏,即使在最简单的单轴压缩条件下亦是如此。因此,岩石的变形破坏细观上表现为岩石内部空隙结构的扩张、贯通、滑移的不断演化和发展,研究岩石变形破坏特征和机理是目前岩石力学的复杂难题之一。

岩石变形破坏模拟试验经常采用的方法有有限元、离散元、有限差分法等,尤其是有限元方法具有技术成熟、计算效率高等优点,当前主要的问题聚焦在破坏指数的确定方面,关于岩石破坏指数的研究已有不少成果,主要是依据岩石强度理论发展而来。因此,选取合理的数值计算方法,并依据合理岩石强度破坏准则与指标来判断岩石受力过程中的破坏特征,对研究岩石变形破坏规律具有非常重要的意义。

基于此,本文将利用有限元数值模拟方法研究不同微裂隙条件下岩石试样单轴压缩时其内部压剪破坏指数和拉伸破坏指数的分布规律及特征,探讨微裂隙面和受力方位相对关系及不同微裂隙组合对岩石破坏倾向的影响程度。研究将对岩石变形破坏机理的深入具有推进作用。

1 分析模型及试验方案

1.1 分析模型

理论上,单轴压缩条件下均质岩样的受力特征为同一应力状态,但实验室试验过程中一般无法完全克服压力机的端头摩擦效应,致使实际的岩石试验结果或多或少地受端头摩擦效应的影响。在本文的数值模拟过程中,基于理想的单轴压缩试验,建立数值计算模型及边界条件。模型宽50 mm,高 100 mm,下边界限制竖直方向的位移,上边界给一竖向位移,模拟压力机的位移控制压缩试验。试验中采用传统弹塑性本构模型,忽略与时间相关的因素。

1.2 试验方案

大量试验研究和理论分析成果表明,岩体内部微裂隙的形状、尺寸和受力方位对于岩体的变形和破坏具有控制作用。本次试验考虑能反映岩石试样损伤特征的椭圆缝裂隙,试验方案共6组,如图1所示。

数值模拟计算中岩石的力学参数,以沁水煤田西河煤矿3#煤层的力学特性为工程对象,其中煤的弹性模量500 MPa,单轴抗压强度9.8 MPa,黏聚力1.5 MPa,内摩擦角30°。竖向压缩位移控制为2 mm。

2 破坏指数的分布特征及规律

现有岩体破坏理论研究成果表明,岩石的破坏主要分为压剪破坏和拉伸破坏两种模式。本文基于岩体压剪破坏机理和拉伸破坏机理构建岩体破坏指数,包括压剪指数和拉伸指数。压剪指数为岩体在摩尔-库伦准则下材料的应力状态压缩指数与综合抗压强度的比值,其值越大破坏指数越高,岩体压剪破坏的倾向性越强;拉伸指数为岩体在格里菲斯准则下材料的应力状态拉伸指数与综合抗拉强度的比值,其值越大破坏指数越高,岩体拉伸破坏的倾向性越强。

2.1 岩样的压剪指数

模拟得到不同方案条件下岩样的压剪指数分布图,如图2所示。

图2 不同方案下压剪指数分布

从图2中可以看出,方案1在圆孔裂隙周围出现压剪指数集中区域,分布呈现孔上∨形、孔下∧形分布特征,证明此种圆孔裂隙分布的岩样其压缩破坏具有沿孔径在倾斜方向滑移破坏的趋势,破坏形式为锥形,与一般无裂隙试样的单轴压缩破坏相类似。方案2在裂隙周围出现椭圆环形压剪指数集中区域,表明在压缩载荷的作用下原始的裂隙形成长轴与短轴比更小的椭圆孔洞。方案3在裂隙周围出现明显的X形,表明破坏沿裂纹的尖端倾斜扩展,具有典型的锥形剪裂破坏倾向。方案4压剪指数分布呈现S形特征。方案5和方案6压剪指数分布和方案4基本相同。

压剪指数分布特征表明圆孔裂隙呈现上∨下∧形压剪指数集中区;水平裂隙呈现椭圆环形压剪指数集中区;竖直裂隙压剪指数集中区域呈现X形;斜裂隙压剪指数集中区域呈现S形。

2.2 岩样的拉伸指数

模拟得到不同方案条件下岩样的拉伸指数分布,如图3所示。

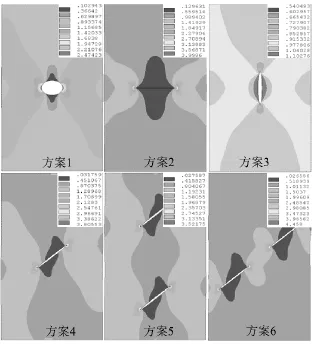
图3 不同方案下拉伸指数分布

由图3可知,方案1在圆孔裂隙周围出现压剪指数集中区域,分布在圆孔两侧,呈X形向四周展开,据此推断拉应力效应会使岩样压缩试验产生典型的锥形破坏形态。方案2、方案3和方案1的特征基本相同,均表现为具有锥形破坏形态的倾向。方案4和方案5拉伸指数集中区域分布呈现近似竖向分布,据此推断拉应力效应会产生岩石力学试验典型的柱状劈裂破坏形态。方案6两条裂隙拉伸指数集中区域具有连通性,据此推断破坏将为受裂隙控制的典型单向剪切破坏。

拉伸指数分布特征表明圆孔裂隙、水平裂隙、竖直裂隙周围呈现X形拉伸指数集中区,具有X型破坏特征;单个斜裂隙、竖向方向倾斜裂隙组周围呈现近似竖向区域拉伸指数集中区,具有竖向张裂破坏特征;斜向方向倾斜裂隙组周围呈现近似倾斜区域拉伸指数集中区,具有单向滑动破坏特征。

基于两个强度理论的数值模拟计算表明,无论是哪种指数,单轴压缩试验的破坏形态特征都表现为锥形剪裂、柱状劈裂和单向剪切3种形式,该试验结论与实验室岩石单轴压缩试验的测试结果基本一致。

3 裂隙分布形态对破坏指数的影响

前面的分析获得了不同裂隙形态下压剪指数和拉伸指数分布特征及可能出现的破坏特征,然而,不同裂隙分布形态下不仅破坏指数分布规律不同,其破坏指数的数值亦有巨大差异。基于此,分析不同裂隙分布形态下压剪指数极值、拉伸指数极值以及拉伸指数极值与压剪指数极值比的规律,为试件稳定性状况分析和破坏倾向性程度判断提供依据。

不同方案条件下拉伸指数最大值柱状图见图4所示。据图4可知,拉伸指数最大值从小到大依次为方案3＜方案1＜方案4＜方案2＜方案5＜方案6,亦即竖直裂隙＜圆孔＜单个斜裂隙＜水平裂隙＜竖向方向倾斜裂隙组＜斜向方向倾斜裂隙组。

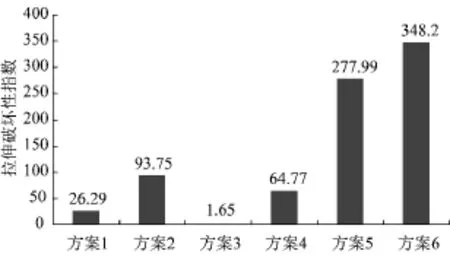
图4 不同方案下最大拉伸指数

不同方案条件下压剪指数最大值柱状图如图5所示。据图5可知,压剪指数最大值从小到大依次为方案3＜方案1＜方案5＜方案4＜方案2＜方案6,亦即,竖直裂隙＜圆孔＜竖向方向倾斜裂隙组＜单个斜裂隙＜水平裂隙＜斜向方向倾斜裂隙组。

不同方案条件下拉伸指数最大值与压剪指数最大值比柱状图如图6所示。由图6可知,其数值特征从小到大依次为方案3＜方案1＜方案4＜方案2＜方案6＜方案5,亦即竖直裂隙＜圆孔＜单个斜裂隙＜水平裂隙＜斜向方向倾斜裂隙组＜竖向方向倾斜裂隙组。

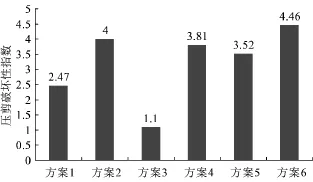
图5 不同方案下最大压剪指数

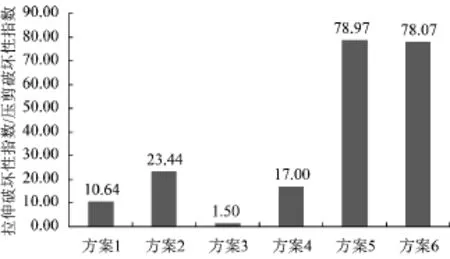
图6 不同方案下最大拉伸指数与压剪指数比

现场实际中岩体内部存在各种形态的裂隙,对其分类可以近似分为圆形裂隙、水平裂隙、竖向裂隙和倾斜裂隙的组合,其破坏受关键裂隙组的控制。综合分析可知单轴压缩条件下,裂隙岩体的破坏主要由拉应力引起。倾斜裂隙组更容易引起岩石试件破坏,破坏特征呈现典型的沿单一倾斜面。其次为竖向倾斜裂隙组与单个倾斜裂隙,破坏特征呈现典型的平行于加载方向的多个破裂面。最后为竖向裂隙、水平裂隙及圆孔隙,破坏特征为典型的双锥形破坏面。

大量的试验研究表明岩石在单轴压缩条件下破坏特征出现的概率具有单斜面破坏＞竖向面破坏＞锥形面破坏,这是由于岩体内部存在大量的裂隙组,同等条件下斜向倾斜裂隙组的控制作用大于竖向倾斜裂隙组,且后者大于单个裂隙。这种表现形式与本文分析所得结论完全一致。

4 结论

(1)岩体内部存在大量各种形态的裂隙,可以近似简化为圆形裂隙、水平裂隙和倾斜裂隙的组合,其破坏程度和形态将受发育程度最高的关键裂隙组控制。

(2)裂隙岩体在单轴压缩条件下破坏特征出现的概率具有单斜面破坏＞竖向面破坏＞锥形面破坏的特征。

(3)单轴压缩条件下,裂隙岩体的破坏主要由衍生的拉应力引起。

[1] 蒲成志,曹平,赵延林等.单轴压缩下多裂隙类岩石材料强度试验与数值分析[J].岩土力学,2010 (11)

[2] 杨圣奇.断续三裂隙砂岩强度破坏和裂纹扩展特征研究[J].岩土力学,2013(1)

[3] 任利,谢和平,谢凌志等.基于断裂力学的裂隙岩体强度分析初探[J].工程力学,2013(2)

[4] 吴刚,孙钧.卸荷应力状态下裂隙岩体的变形和强度特性[J].岩石力学与工程学报,1998(6)

[5] 范雷,周火明,张宜虎.微裂隙对工程岩体强度参数的影响分析[J].岩石力学与工程学报,2011 (S1)

[6] 韩建新,李术才,李树忱等.贯穿裂隙岩体强度和破坏方式的模型研究[J].岩土力学,2011(S2)

[7] 杨建平,陈卫忠,伍国军等.基于有限元方法的裂隙岩体等效强度参数研究[J].岩石力学与工程报,2011(S2)

[8] 冯增朝,赵阳升.岩体裂隙分维数与岩体强度的相关性研究[J].岩石力学与工程学报,2003(S1)

[9] 靳瑾,曹平,蒲成志.预制裂隙几何参数对类岩材料破坏模式及强度的影响[J].中南大学学报(自然科学版),2014(2)

[10] 张成文,吕坤,贺瑞彬等.复杂顶板条件下巷道合理支护参数研究[J].中国煤炭,2016(5)

[11] 孙晓元,董利辉,孙英峰等.掘进工作面突出瓦斯运移扩散特性模拟研究[J].中国煤炭,2015 (4)

[12] 肖桃李,李新平,贾善坡．深部单裂隙岩体结构面效应的三轴试验研究与力学分析[J]．岩石力学与工程学报,2012(8)

[13] 黄达,黄润秋．卸荷条件下裂隙岩体变形破坏及裂纹扩展演化的物理模型试验[J]．岩石力学与工程学报,2012(3)

Numerical simulation study on relationship between micro-fissuring distribution and uniaxial compression failure of rock samples

He Yaoyu1,Song Xuanmin1,Xing Pingwei2
(1.Institute of Mining Technology,Taiyuan University of Technology,Taiyuan,Shanxi 030024,China; 2.School of Continuing Education,Taiyuan University of Technology,Taiyuan,Shanxi 030024,China)

By adopting numerical simulation with finite elements,numerical simulation test of uniaxial compression was carried out to study the different fissuring distribution of rock samples.Though introducing compression-shear index and stretch index to estimate the failure of rock samples,failure characteristics and tendency of rock samples with different fissuring conditions were analyzed,and failure mechanism and influencing rule of the rock samples with fissuring were discussed.The results showed that under the condition of uniaxial compression,the failure of normal rock sample with fissuring was mainly controlled by tensile stress,and the appearance probability of monoclinic failure plane was greater than that of vertical failure plane,and which was greater than that of subulate failure plane,and the results were agree with lots of tests,it explained the failure process of rock with fissuring under the uniaxial compression in mechanism.

failure of roak sample,micro-fissuring of rock sample,fissuring form,uniaxial compression,failure index,numerical calculation

TD313 TU452

A

何耀宇(1974-),男,山西霍州人,博士研究生,主要从事岩石力学研究工作。

(责任编辑 张毅玲)

山西省联合基金项目(2012012012)