基于高斯过程分类的堤基管涌发生可能性识别方法

肖义龙林利森赵 鹏

（1.江西省水投华东设计有限公司，江西南昌 300029；2.江西省安澜工程咨询有限公司，江西南昌 330001；3.西安中粮工程研究设计院有限公司，陕西西安 710082）

基于高斯过程分类的堤基管涌发生可能性识别方法

肖义龙1林利森2赵 鹏3

（1.江西省水投华东设计有限公司，江西南昌 300029；2.江西省安澜工程咨询有限公司，江西南昌 330001；3.西安中粮工程研究设计院有限公司，陕西西安 710082）

管涌是导致堤基渗透变形破坏的主要原因之一，其影响因素众多且各因素之间又存在高度的非线性关系。因此，本文提出了一种基于高斯分类模型的堤防管涌发生可能性识别的新方法。首先，通过数学实例对比展示该方法的优越性，进而将该方法应用于工程实例中，结果表明该方法是可行的，且模型具有参数自适应确定、容易实现且识别精度高等优点，对于迅速识别堤基管涌发生的可能性具有重要的实际应用价值。

高斯过程分类；堤防工程；管涌识别；机器学习

江西省境内水系发达，河流众多，其中赣江、抚河、信江、饶河和修河统称“五河”。江西省计划投资约135.3亿元治理“五河”，其中堤线长度达到1848km，是江西省有史以来水利“打捆”最大的工程项目。截至2007年底，全省建成堤防4000余条，堤防总长9753km。可见堤防的后期管理和维护工作任务重，能够高效、准确地识别出危险堤段就显得尤其重要。然而，导致堤段出现险情（堤防失稳、坍塌、溃堤等）的主要原因就是堤基的渗透变形破坏，其中管涌［1］便是渗透变形的主要类型。因此，及时、准确判定和预报堤防工程管涌险情对于防汛抢险、保护人民生命财产安全具有重要的社会和经济效益。

近年来，国内外学者针对管涌的判定和识别提出了不同的方法，如水头分析法［2］、室内模型试验法［3］、管涌数值模拟法［4-5］等。以上传统方法由于受到试验条件、模拟条件假设等方面的限制，很难将多种影响因素综合考虑。一些学者将人工智能方法如BP人工神经网络［6-7］、支持向量机［8］等应用于堤基的管涌可能性识别，较传统方法有了一定的突破，但是鉴于这些方法本身还存在着一些不完善之处，如神经网络的过分依赖样本质量、拓扑结构不稳定等，支持向量机的核函数、损失函数等参数难以确定，为此，有必要探讨一种新的管涌发生可能性识别方法。

高斯过程机器学习方法是近年来发展起来的一种新的人工智能方法，凭借严格的统计学习理论体系，在处理高度非线性、少样本等复杂的问题中表现出显著的优势［9-10］，现已成为国际人工智能研究领域的热点。

因此，本文通过高斯过程机器学习方法中的二元分类模型构建管涌内部各因素之间的非线性映射关系，通过分类方法识别出管涌发生的可能性，为堤基管涌提前预判提供了一条解决途径。

1 GPC模型的基本原理

高斯过程机器学习方法的理论基础是高斯随机过程与贝叶斯学习理论。高斯过程二元分类（Gaussian Process for Binary Classification，GPC）模型是高斯过程机器学习方法的一种应用，另外一种是高斯过程回归模型［11］。

在GPC模型中，设一个随机变量x相对应的输出值为二元分类标签y，y∈｛-1，1｝。GPC模型的目的就是通过学习一定数量的样本构建随机变量与分类标签之间的映射关系，随后对测试随机变量x*进行分类识别出对应的标签y*。

对于确定的x，p（y|x）服从伯努利分布，y=1的概率为

其中，f（x）称为潜在函数；Φ（·）称为标准高斯分布的累计概率密度函数，一般取sigmoid函数

利用该函数的目的主要是将区间约束f（x）转换为［0，1］区间的函数值，从而保证概率值落在［0，1］区间。

假设fi=f（xi），f=［f1…，fm］T，y=［y1…，ym］T，X=［x1…，xm］T。对于给定的潜在函数f，观察值y是服从独立的伯努利分布，其似然函数为

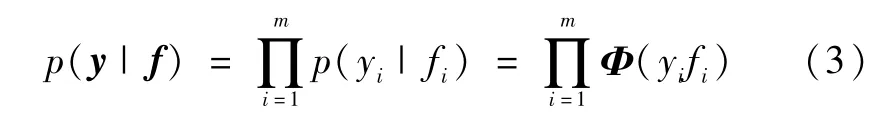
潜在函数f的先验分布满足

其中，K为m×m阶协方差矩阵，Kij=k（xi，xj，θ）；K（ ）表示与θ有关的正定协方差函数；θ称为超参数。

常用的协方差函数为

其中，θ=｛l，σf｝称之为超参数，可由极大似然法自适应获得［12］。

通过不断获得实测值后，依据贝叶斯理论，潜在函数f的后验分布为

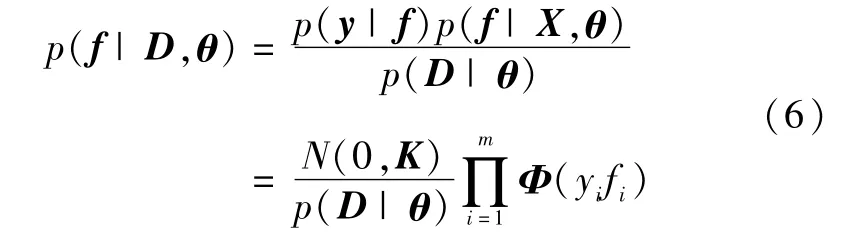
注意上式中潜在函数f的后验分布并非满足高斯分布。

与x*对应的潜在函数值f*的条件概率为

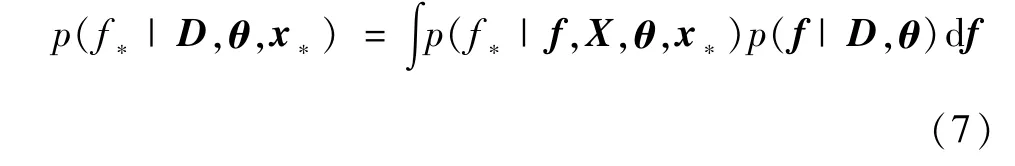
y*的预测概率为

当y*的预测概率值大于0.5时，y*=1，否则y*=-1。

但是，当式（6）、式（7）和式（8）均没有解析解时，可采用Expectation Propagation法求得近似解［12］，则f的后验分布的近似分布满足

m和A对应近似解的均值和方差，潜在函数f后验分布的近似高斯分布满足

其中，μ=（μ1，…，μm），Σ=diag（）。

同样，f*的后验分布可假设满足近似的高斯分布

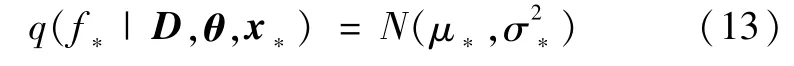
其中的均值和方差为

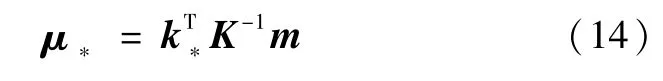
其中，k*=［k（x1，x*），…，k（xm，x*）］T表示x*与学习样本随机变量X之间的先验协方差矢量。

由非高斯分布转换为近似高斯分布的逼近方法处理后，就可以获得x*属于第1类的预测概率解析解

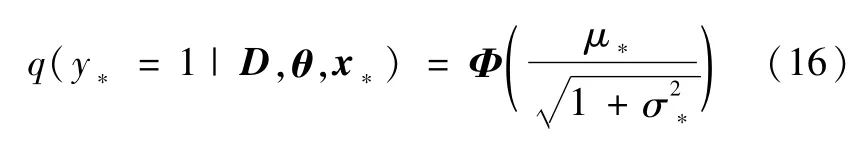
当q＞0.5时，y*=1，否则y*=-1。

2 GPC的性能测试

为了更好地反映出GPC模型在处理少样本、高度非线性等复杂问题上具有良好适应性，在此首先针对数学函数进行测试［12］：

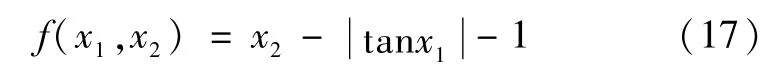
首先学习样本的随机变量x1∈［0，7］、x2∈［0，6］在各自范围内等间距离散取14个数值，并两两组合成196个随机变量X，然后对其函数值进行识别，如f（X）＞0，则对应取标签1；否则取标签-1。从而构建GPC模型的196个学习样本。初始超参数为（1，1），设置共轭梯度优化算法最大迭代步数为200，计算所得的最优超参数为：l=1.1742，σf= 204.7967。最后通过已经建立的GPC模型对函数进行拟合，其效果见下图（a）。

采用GPC拟合时，其拟合效果较支持向量机［13］有一定的提高，同时不存在参数选择难等问题，其主要原因是模型对应的最优超参数都是通过极大似然法自适应获取的。因此，GPC模型对于这种高度非线性函数的分类边界拟合精度较SVM有明显提高，见下图（b）。

模型的分类边界拟合效果对比图

3 工程实例研究

3.1 主要影响指标的确定

对于堤基管涌的发生机理国内外学者研究众多，其中大部分学者［1-5］认为影响显著的因素包括坝高H、坝前水深Hp、下游边坡坡比m、土的有效黏聚力c、有效内摩擦角φ、饱和单位容重γ、渗透系数K、最大有效粒径db、下游滤层倾角δ共9个。

3.2 GPC模型建立步骤

a.利用文献［6，8］中提供的17组数据资料建立学习样本（xi，yi）（i=1，2，…，9），其中输入随机变量xi代表影响管涌发生可能性的9个主要影响因素数值，输出量yi将堤防管涌发生可能性λ识别分为管涌稳定（输出标签为1）、管涌破坏（输出标签为-1）。

b.为了更好地消除因素之间的数量级差异，使GPC模型获取更好的学习效果，有必要对学习样本进行标准化处理：

c.由GPC模型对学习样本进行学习，获得适合学习样本的最优超参数l、σf。

d.利用训练成功的GPC模型对测试随机变量x*进行管涌发生的可能性识别类型y*。

3.3 识别效果分析

采用文献［8］中表2的6个试验数据作为测试样本，见下表。

对学习样本进行学习，超参数初始值假设为（1，1），以训练样本的极大似然为目标，采用共轭梯度优化算法搜索最优超参数。设置收敛标准为最大迭代步数为200。获得最优超参数值：l=3.8017，σf= 52.7776。

GPC分类模型的可能性识别结果见下表，从中可以看出，GPC模型对堤防管涌发生可能性识别准确，评估结果与实际结果非常吻合。因此，将GPC分类模型用于堤防管涌发生可能性识别是可行的，并且由于GPC模型相比SVM分类模型不受参数设置的限制，更有必要将该方法引入到堤基管涌可能性发生的识别中，使其尽早在实际工程应用中发挥应有的经济效益。

堤防管涌识别模型测试样本表

4 结 语

a.传统方法由于受现场条件和试验假设的影响，难以较好地处理堤基管涌与9个主要影响因素之间的高维度非线性关系，而高斯过程机器学习方法凭借其严格的统计理论基础实现了高精度地拟合这种非线性关系。实例分析表明，GPC分类模型是可行的，并且可以给出准确可靠的分类结果，实现了对管涌发生可能性作出提前识别。

b.GPC分类模型虽然可以较好地处理学习样本少的分类问题，但是，要想获得更好的识别精度，学习样本的质量是至关重要的。因此，在工程实际应用中，如何获取高质量的样本来完善自身的学习样本资料库值得作进一步深入的研究。

c.高斯过程机器学习方法凭借其严格的统计理论基础、超参数自适应获取等优点，现已成为人工智能方法领域的研究热点。因此，在工程类型判别方面拥有广泛的应用前景［14-15］。

［1］ 毛昶熙，等.堤防工程手册［M］.北京：中国水利水电出版社，2009：35-40.

［2］ CHEN Yifeng，HU Ran，ZHOU Chuangbing，etal.A new parabolic variational inequality formulation of Signorini’s condition for nonsteady seepage problems with complex seepage control systems［J］. International Jounrnal for Numerical and Analttical Methods in Geomechanics，2011（35）：1034-1058.

［3］ 李广信，周晓杰.堤基管涌发生发展过程的试验模拟［J］.水利水电科技进展，2005，25（6）：21-24.

［4］ 周健，白彦峰，姚志雄.管涌型土滤层防治的细观试验研究［J］.水利学报，2010，41（4）：390-397.

［5］ 张刚.管涌现象细观机理的模型试验与颗粒流数值模拟研究［D］.同济大学，2007：32-40.

［6］ 张我华，余功栓，蔡袁强.堤与坝管涌发生的机理及人工智能预测与评定［J］.浙江大学学报（工学版），2004，38（7）：902-908.

［7］ 赵正信，陈建生，陈亮.无黏性土管涌型土的BP神经网络判别法研究［J］.岩土工程学报，2008，30（4）：536-540.

［8］ 翟越，刘浪，于澍.堤防管涌发生可能性识别的网格搜索——支持向量机方法［J］.中南大学学报（自然科学版），2015，46（4）：1497-1503.

［9］ 张研，苏国韶，燕柳斌.水库水温分布结构识别的高斯过程机器学习方法［J］.水利水电科技进展，2009，29（2）：13-15，39.

［10］ 彭立峰，苏国韶，王志成，等.基于高斯过程分类与蒙特卡洛模拟的岩土工程结构可靠度分析方法［J］.科学技术与工程，2013，13（21）：6150-6156.

［11］ 林利森，肖义龙.基于高斯过程的混凝土强度预测［J］.江西水利科技，2014，40（3）：219-223.

［12］ KUSS M，RASMUSSEN C E.Assessing approximate inference for binary Gaussian process classification［J］.Journal of machine learning research，2005（6）：1679-1704.

［13］ Anirban Basudhar，Samy Missoum，Antonio Harrison Sanchez.Limit state function identification using Support Vector Machines for discontinuous responses and disjoint failure domains［J］.Probabilistic Engineering Mechanics，2008（23）：1-11.

［14］ 苏国韶，陈光强，吕海波.高斯过程机器学习在膨胀土等级分类中的应用［J］.路基工程，2009，2（143）：1-2.

［15］ 张研，苏国韶，燕柳斌.基于高斯过程机器学习的岩爆等级识别方法［J］.地下空间与工程学报，2011，7（2）：392-397.

Identification method of levee foundation piping possibility based on Gaussian process classification

XIAO Yilong1，LIN Lisen2，ZHAO Peng3
（1．Jiangxi Shuitou East China Design Co.，Ltd.，Nanchang 300029，China；2．Jiangxi Anlan Engineering Consulting Co.，Ltd.，Nanchang 330001，China；3．Xi′an Cofco Engineering Research and Design Institute Co.，Ltd.，Xi＇an 710082，China）

Piping is one of main causes of levee foundation seepage deformation and destruction.It is affected by many factors，and there is a highly nonlinear relationship among all factors.Therefore，a new method of recognizing levee piping possibility based on Gaussian disaggregated model is proposed.Firstly，the superiority of the method is displayed through math example contrast，thereby the method is applied in engineering example.The result shows that the method is feasible，the model has advantages of parameter adaptive determination，easy realization，high recognition precision，etc.It has important practical application value to quickly recognize the possibility of levee foundation piping.

Gaussian process classification；levee engineering；identification of piping；mechanical learning

TV871

B

1673-8241（2016）09-0055-04

10.16617／j.cnki.11-5543／TK.2016.09.013