基于模糊层次分析法的闹德海水库大坝安全评价
2016-12-06冯秀红
冯秀红
(辽宁省闹德海水库管理局,辽宁阜新 123000)
基于模糊层次分析法的闹德海水库大坝安全评价
冯秀红
(辽宁省闹德海水库管理局,辽宁阜新 123000)
本文基于闹德海水库大坝监测资料和《水库大坝安全评价导则》(SL 258—2000),运用模糊层次分析法建立了闹德海水库大坝安全评价模型,该模型同时考虑影响水库大坝安全的定量因子和定性因子,运用模糊层次分析法确立了各影响因子的权重,定量地实现了水库大坝安全评价。通过实际工程应用,验证了此方法的有效性,为大坝安全风险的控制及评价提供了科学依据。
闹德海水库;模糊层次分析法;大坝安全评价
我国水库大坝数量在世界上首屈一指。为维护水库大坝的安全性和经济效益,保障水库周围人民群众的切身利益和人身安全,维护当地社会的稳定,促进区域的经济快速发展,对水库大坝的安全性作出合理评价显得尤为重要[1]。
目前,我国实施的《水库大坝安全评价导则》(SL 258—2000)中,对水库大坝的安全评价作出了明确的规范,主要从防洪安全性、结构安全性和抗震安全性三个方面,对水库大坝的安全性进行综合分析研究[2]。但导则中影响大坝安全的因子多为定性因子,无法对水库大坝安全作出定量评价。本文以闹德海水库为工程背景,基于模糊层次分析法,提出相对较好的解决办法,实现水库大坝安全稳定性的定量化评价。
1 模糊层次分析法简介
模糊层次综合评价法(FAHP)是20世纪70年代美国运筹学T.L.Saaty教授提出的一种定性与定量相结合的系统分析方法。它以模糊数学理论和层次分析法为基础,引入模糊数学中的“隶属度”,用隶属函数对具有模糊性的指标进行处理。模糊数学评价用隶属函数描述方案的得分来量化指标实测值,可以较好地解决综合评价中的模糊性(如因素类属之间的不清晰性、专家认识评价上的模糊性等),可最大限度地减少人为因素。另外,与最初的层次分析法相比,模糊层次分析法可以为我们提供更加方便合适的选择,在水库大坝安全性评价方面也比较新颖,能够从另一种角度完成定量化评价。
1.1 主要评价思路
主要评价思路是:首先对影响水库大坝安全的因素进行归纳和总结,确定最核心的方面,然后利用层次分析法建立相应的数据模型;再在已经确定的评价因素、因子的评价等级标准和权值的基础上,运用模糊数学知识原理,构造模糊评价矩阵,对该矩阵进行多层的复合运算,最终确定评价目标的等级。
由于影响水库大坝安全性的因素很多,而且各种影响因素随机组合,并且没有明确的影响程度大小,另外,每个因素之间又存在相互隶属关系或者并列关系,层次繁多,进行安全性评价时,比较难于得到准确唯一的结论。因此针对大坝的这些特点,本文采用模糊层次评价方法,得到模糊集,进而完成最终的综合评价。
1.2 主要步骤
1.2.1 建立层次结构模型
按照前文提到的导则为主要依据确定层次结构模型[3],该模型主要可以将水库大坝安全评价体系分为三个层次:第一层为目标层,主要针对为水库大坝安全评价;第二层为准则层,包含导则中明确规定的七个方面,例如工程质量评价、大坝运行管理评价、防洪标准复核、结构安全评价、渗流安全评价、金属结构和抗震性能复核;最后一层为因素层,包含各种影响大坝安全的因素[4]。因此可以得到如图1所示的结构层次图。
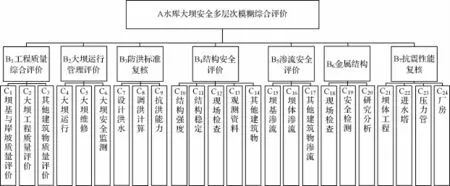
图1 大坝安全评价结构层次模型
1.2.2 确定权重集
前文提到,因大坝的安全评价十分复杂,涉及到的因素又很繁杂,其对大坝的安全性影响程度也不同,因此必须确定这些影响因素的相应权重。在上述的层次分析法中,我们将影响因素两两比较,得到相应的权值,最后得到最终的安全评价权重集W。
1.2.3 确定评价集
评价集指的是评价者对相应评价对象作出的各种评价结果所组成的集合,用V来表示[5]。它一般是由评价人根据现实情况确定,划分的等级一般在3~9级之间,即评价集V={V1,V2,Vm}(3≤m≤9)。在大坝安全评价中,可以令V={V1,V2,V3},各评语分别代表{安全,安全性一般,不安全},由高到低表示安全程度。
1.2.4 建立判断矩阵
模糊层次分析法最主要的内容是评价人按照前面建立的层次模型中的每个因素的相对重要性作出具体的判断,这些判断的结果利用相应的标度进行表示,主要是用数值1~9,最后写成判断矩阵R(单项指标),1~9标度的具体含义见表1。

表1 1~9标度的含义
其中
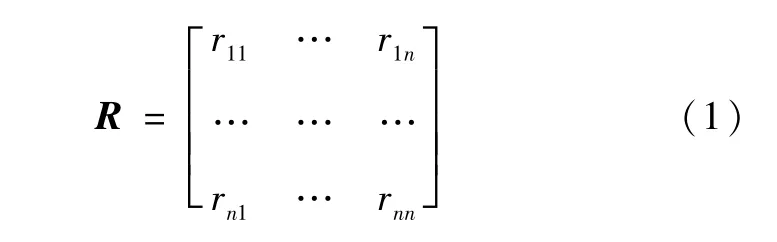
1.2.5 综合评价
模糊层次综合评价的主要原则是:先从最低层开始进行评价,并将每层的评价结果看作是上一层因素的评价集,再组成更高一层的因素评价矩阵,再对高一层进行综合评价,直到完成所有的评价[6]。这就要求我们在建立相应的层次结构模型时,必须考虑每一层因素中的相互独立性,不能存在依赖关系。所以各层应该保持一致的综合评价算法,模型如下:
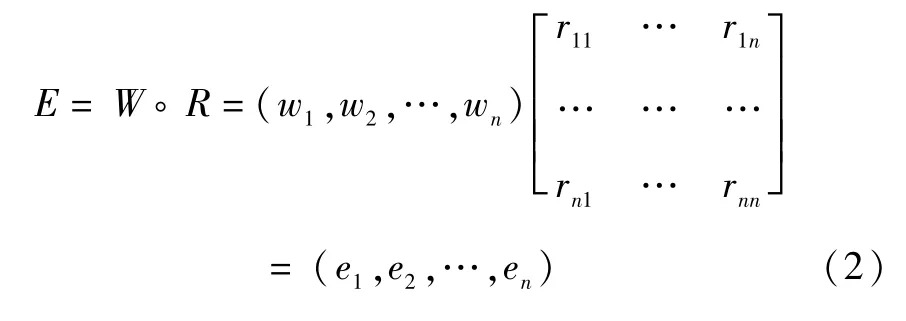
在式(2)中,“°”表示模糊综合运算符,称为模糊算子。它有许多形式,其中最常用的是“取大取小算子”和“乘与和算子”。按照上述的方法,从最低一层开始不断进行模糊运算,最终得到总体模糊评价集E=(e1,e2,…,en),归一化后得E′=(e′1,e′2,…,e′n),其中

1.2.6 得到最终评价结论
在完成以上的计算后,可以得到具体的计算结果,最后通过总体评判集E′,根据最大隶属度原则对大坝安全性作出评估,给出合理的评价结论。
2 实例分析
2.1 工程概况
闹德海水库位于辽宁省阜新市彰武县西北部柳河中游,是一座防洪滞沙、农田灌溉、工业供水等综合利用的大(2)型水库,是柳河上唯一已建大型控制性工程。水库建设于伪满年代,于1942年10月竣工,历经70余年,进行了四次加固改造。
该工程为Ⅱ等工程,主要建筑物为2级。水库枢纽工程由挡水坝段、溢流坝段、排沙中孔、底孔和输水洞等建筑物组成。大坝为混凝土重力坝,坝顶高程194m,坝顶宽度5m,最大坝高44.5m,大坝总长167m,溢流坝段长75m,堰顶高程181.5m。溢流坝段设有五个排沙底孔,孔底高程151m,尺寸为1.7m×2.35m;溢流坝段左侧设有两个排沙中孔,孔底高程163m,尺寸为1.7m×1.85 m。输水洞距离右坝头50m,进口高程164.8m,洞径3m,向阜新提供工业和生活用水。
2.2 安全评价
2.2.1 建立层次结构模型
按照前文的步骤,对闹德海水库大坝进行安全评价时,先建立相应的模型,主要参考图1。
2.2.2 确定权重集
根据层次分析法,在确定其各个影响因素的权重值时,首先从最低一层也就是因素层开始,根据各个因素对上一层的重要程度,相互比较确定孰轻孰重得到评判矩阵,利用数学方法求出各因素的权值并归一,然后通过一致性检验后得到因素层对准则层的权重集[7]。然后,采用相同的方法确定准则层对目标层的权重集。为了接下来表述方便,权重集均用Wij来表示,下标i=1为准则层对目标层的权重集,i=2为因素层对准则层的权重集;下标j代表被评价指标的编号,当只有一个指标时,可以省去j。权重集对各工程应是通用的[8]。
根据各专项的安全性评价,按图1的层次结构,构造判断矩阵,并用方根法计算相应的权重,得到如表2所列的结果。

表2 判断矩阵A—B数值
根据上表可得WA={0.290,0.045,0.137,0.290,0.073,0.027,0.137},之后同理可依次得到每一层的权重,WB1={0.279,0.649,0.072},WB2={0.088,0.243,0.669},WB3={0.333,0.333,0.333},WB4={0.397,0.397,0.092,0.076,0.037},WB5={0.661,0.272,0.067},WB6={0.637,0.258,0.105},WB7={0.636,0.230,0.089,0.045},最后对上述结果进行检验,确定各判断矩阵满足一致性,因此不需要再进行调整。
2.2.3 确定评语集
在颁布的导则中,安全性的评价采用A、B、C三级,依次表示安全、基本安全、不安全[9]。为了和导则保持一致,方便模糊层次分析法的推广和应用,本文对评价对象的评语也采用3级,为{安全,基本安全,不安全}[10]。
2.2.4 建立评价矩阵
建立评价矩阵时,需要评价者进行打分,打分的主要依据是闹德海水库近段时间的监测数据及分析结果。
2.2.4.1 巡视检查情况
工程管理处按照右岸、左岸、坝顶、廊道的路线进行现场检查,每月2次,主要检查坝体表面有无裂缝、脱落、滑动及异常变形。2016年一季度现场检查未发现异常情况。
a.水平位移监测分析。坝顶水平位移监测采用真空激光准直系统和倒垂线组合方式。激光准直系统布置在坝顶上游侧,共设11个测点。用于监测各坝段的水平位移,测点编号为LA1~LA10。与此同时,在紧靠激光准直监测系统端点处布设2套倒垂线,作为激光准直系统端点的工作基准,将相对水平位移校正为绝对位移。水平位移向下游为正,向上游为负。
根据监测结果可以得到:坝体最大水平位移为-7.95mm(向上游),对应测点为LA2,发生在2016年1月27日;坝体最大水平位移变化量为2.62mm,对应测点为LA4。
过程线见图2~图5,从图中可知,2016年1—3月各测值正常,水平位移不大,变化较小,且与往年同期变化趋势基本相同。

图2 主坝水平位移过程线(一)
b.垂直位移监测分析。坝顶垂直位移采用真空激光准直系统和双金属标组合方式进行监测,真空激光准直监测系统布置在坝顶上游侧,共11个测点,用于监测各坝段的垂直位移,测点编号为LA1~LA10;2套双金属标位于激光准直系统两端点附近,作为激光准直系统端点的工作基准,将相对垂直位移校正为绝对位移。垂直位移向下为正,向上为负。

图3 主坝水平位移过程线(二)

图4 主坝水平位移过程线(三)

图5 主坝水平位移过程线(四)
根据监测成果可以得到:坝体最大垂直位移为14.29mm,对应测点为LA3,发生在2016年2月24日;坝体最大垂直位移变化量为13.68mm,对应测点为LA5。
过程线见图6~图9,从图中可知,该季度各测点测值均有一定的变化,其中LA2~LA8比其他测点变化大,最大变化量为13.68mm。各测点过程线的“毛刺”现象,可能与自动化采集误差有关。

图6 主坝垂直位移过程线(一)
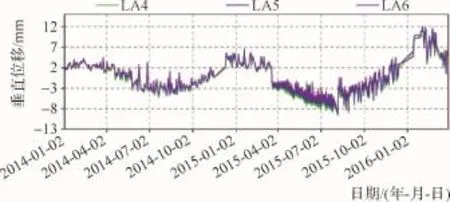
图7 主坝垂直位移过程线(二)

图8 主坝垂直位移过程线(三)

图9 主坝垂直位移过程线(四)
2.2.4.3 渗流监测分析
a.坝基扬压力监测分析。横向扬压力监测分析:
沿坝基布置2个横向扬压力监测断面,分别布设3个测点,共6个测点,用于监测坝基横向扬压力。测点编号为UP2-1、UP2-2、UP2-3、UP9-1、UP9-2、UP9-3。
第二,不仅应当切实立足实际的教学活动,也应超出各个具体内容并从更一般的角度去思考相关研究的意义,即是真正做到“小中见大”,用具体的例子说出普遍性的道理,从而真正起到“以点带面”的作用.
根据监测结果可以得到:坝基横向扬压力水位最大值为159.11m(水头高10.11m),发生在2016年1月21日,对应测点为UP2-3;坝基横向扬压力水位最大变化量为3.25m,对应测点为UP9-2。
过程线见图10~图11,从图中可知,各测点扬压力水位总体正常,且明显低于库水位(如扬压力水位最高为159.11m,对应的库水位为175.76m)。除测点UP9-2外,其余测值变化不大,最大变化量为1.61m,说明坝基横向扬压力较稳定。

图10 坝基横向扬压力过程线(一)

图11 坝基横向扬压力过程线(二)
该季度测点UP9-2水位变化较大,最大变化量为3.25m,且有逐渐升高的趋势(可能受库水位升高的影响),但相比往年测值而言,水位不大,建议密切关注该测点测值变化。
纵向扬压力监测分析:
坝基扬压力监测沿纵向断面布置8个测点。采用NVP型振弦式渗压计,用于监测坝基纵向扬压力。测点编号为UP1、UP3、UP4、UP5、UP6、UP7、UP8、UP10。
根据监测结果可以得出:坝基纵向扬压力水位最大值为160.50m(水头高13.5m),发生在2016年3月18日,对应测点为UP10;坝基纵向扬压力水位最大变化量为3.36m,对应测点为UP8。
过程线见图12~图14,从图中可知,该季度各测点扬压力水位与往年水位持平或有所下降,且均明显低于库水位(如扬压力水位最高为160.50m,对应的库水位为176.57m),各测点扬压力水位变化较稳定,说明坝基纵向扬压力较稳定。

图12 坝基纵向扬压力过程线(一)
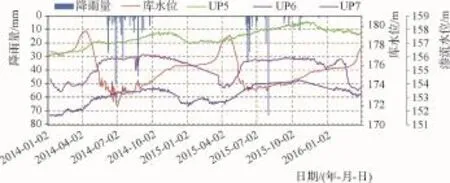
图13 坝基纵向扬压力过程线(二)
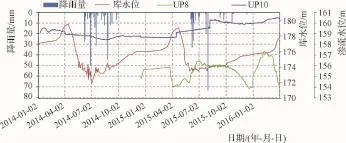
图14 坝基纵向扬压力过程线(三)
b.廊道渗流量监测分析。廊道渗流量监测采用1套量水堰渗流量仪,测点编号为WE1。
根据监测结果可以得出:廊道渗流量最大值为0.006L/s,发生在2016年2月1日。
过程线见图15,从图中可知,该季度渗流量测值较小,变化稳定,无异常现象。

图15 坝体渗流量过程线
c.绕坝渗流监测分析。在坝体左、右岸坝肩分别布置2个监测断面,共4个断面;每个断面布设3个测点,共12个绕坝渗流测点,用于监测绕坝渗流。
根据监测成果可以得出:绕坝渗流水位最大值为177.40m,发生在2016年3月24日,对应测点为R2-4;绕坝渗流水位高程最大变化量为1.37m,对应测点为R2-4。
过程线见图16~图19,从图中可知,该季度各测点测值正常,水位变化趋势与前两年同期基本相同。左岸与库水位相关性较为明显,右岸绕渗测点水位较稳定,变化较小。

图16 绕坝渗流过程线(一)

图17 绕坝渗流过程线(二)
2.2.4.4 环境量监测分析
a.降雨量监测分析。在库区安装1套翻斗式雨量计,用于监测降雨量。
库区雨量站于2015年11月中旬出现故障,至今无法采集到雨量的数据,暂不对降水量进行分析。

图18 绕坝渗流过程线(三)

图19 绕坝渗流过程线(四)
b.库水位监测分析。在主坝安装1套雷达式水位计,用于监测库水位。
库水位过程线见图20,从图中可知,该季度库水位最高为177.70m,发生在2016年3月29日。

图20 库水位过程线
c.气温监测分析。在库区安装1套地表温度计,用于监测库区气温变化,目前采用自动化监测。气温过程线见图21,从图中可知,最高气温为8℃,发生在2016年3月30日。
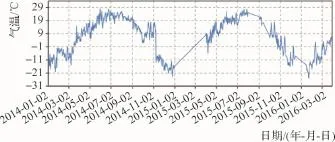
图21 气温过程线
根据闹德海水库的监测数据及分析结果,确定隶属函数的阈值为(3,6,8),评价者对闹德海水库的实际情况打分为U={7,4,3,5,5,3,5,3,2,5,6,4,4,3,6,3,4,3,3,4,6,5,6,4},由此得到的评价矩阵为

2.2.5 模糊综合评价及安全性结果
根据式(2)计算得到各层评价为EB1={0.222,0.788,0},EB2={0.210,0.790,0},EB3={0.500,0.500,0},EB4={0.489,0.511,0},EB5={1,0,0},EB6={0.310,0.690,0},EB7={0.911,0.893,0},大坝的综合评价为EA={0.490,0.510,0}。
为对水库大坝的安全性作出定量评价,把评语集V={安全,安全性一般,不安全}定量化为V=(8,6,3),采用P=EVT来表示水库大坝安全评价指标,显然指标值越大安全性越好[11]。经计算,闹德海水库大坝的安全评价指标值为6.98,按照确定的阀值,属于安全性一般。
3 结 语
a.本文将层次分析法和模糊数学理论整合在一起,建立了大坝安全的多层次模糊综合评价模型,通过闹德海水库大坝的实例应用,证实这种方法科学合理,适合水库大坝的安全性评价。
b.本文提出的大坝安全多层次模糊综合评价法,相比较以往的评价方法有了很大的进步。建立的模糊模型不仅考虑了各专项指标在工程总体上的影响程度,也量化了各种参数指标,较客观地反映了水库大坝的实际情况,相比于现在的方法显得更加合理。
[1] 张小飞,苏国韶,吴彰敦.基于层次模糊综合评价的水库大坝安全评价法[J].广西大学学报(自然科学版),2009(3):321-325.
[2] 岳荣宾.模糊层次和投影寻踪法在大坝安全风险评价中的应用[D].山东大学,2009.
[3] 陈建华.基于模糊数学理论的大坝安全监测系统综合评价研究[D].河海大学,2007.
[4] 张俊涛.小浪底大坝安全监测系统分析与评价[D].河海大学,2007.
[5] 江沛华,汪莲.基于变权的多层次模糊综合评判在大坝安全评价中的应用[J].中国农村水利水电,2010(4):112-114.
[6] 李晓璐,李春雷,李德玉,等.基于多层次模糊分析法的大坝安全评价研究[J].人民长江,2010(17):92-95.
[7] 朱盟.棋盘山水库大坝安全综合评价系统技术研究[D].大连理工大学,2007.
[8] 刘云,王亮,申林方,等.大坝安全风险评价的模糊层次综合模型[J].水科学与工程技术,2007(1):26-29.
[9] 季根蔡.基于层次分析法的水库大坝安全鉴定的综合评价[J].红水河,2007(1):133-136,145.
[10] 吴中如,顾冲时,沈振中,等.大坝安全综合分析和评价的理论、方法及其应用[J].水利水电科技进展,1998(3):5-9,68.
[11] 方卫华.大坝安全的分级评价及其方法[Z]//中国水利学会中国水力发电工程学会中国大坝委员会.水电2006国际研讨会论文集.中国水利学会中国水力发电工程学会中国大坝委员会,2006,7.
Evaluation of Naodehai Reservoir dam safety based on fuzzy analytic hierarchy process
FENG Xiuhong
(Liaoning Naodehai Reservoir Administration,Fuxin 123000,China)
In the paper,fuzzy analytic hierarchy process(AHP)is utilized for establishing Naodehai Reservoir dam safety evaluation model on the basis of Naodehai Reservoir Dam monitoring data and‘Reservoir Dam Safety Evaluation Guidance’(SL 258-2000).Qualitative factors and quantitative factors affecting the safety of reservoir dam are considered in the model at the same time.Fuzzy analytic hierarchy process(AHP)is applied for determining the weights of all influence factors. Reservoir dam safety evaluation is realized quantitatively.The effectiveness of the method is verified through practical project application,thereby providing scientific basis for controlling and evaluating dam safety risk.
Naodehai Reservoir;fuzzy analytic hierarchy process(AHP);dam safety evaluation
TV697
A
1673-8241(2016)09-0035-08
10.16617/j.cnki.11-5543/TK.2016.09.009
