基于禁忌搜索的排课系统的设计
2016-12-05张媛祁兰
张媛,祁兰
(榆林学院 数学与统计学院,陕西 榆林719000)
基于禁忌搜索的排课系统的设计
张媛,祁兰
(榆林学院 数学与统计学院,陕西 榆林719000)
为了实现自动排课,以提高高等学校的工作效率。提出了一种基于禁忌搜索的排课方案,该系统首先采用网络流的处理方法,将排课任务分成若干组;再使用禁忌搜索算法,找到时间和任务组的最优解,从而实现自动排课。实际应用表明,该系统具有使用快捷方便等特点,达到了设计要求。
排课;分组;禁忌搜索;最优化
排课是高校教学管理中一项基本且重要的工作。在教学改革不断深化,教学任务逐年增加的情况下,如何利用有限的资源,实现配置的最优化,有着重要的意义。排课问题是涉及班级、时间、教室、教师等资源的决策优化问题,在排课系统中,处理排课问题所用的算法处于核心地位,由于排课问题本身的复杂性,寻找一个有效的算法还是有相当的难度。
系统采用禁忌搜索算法解决排课问题。首先使用网络最大流算法预处理,把排课任务分成若干组,以保证同一时间内可以进行同一个组的任务,并且教室的供应数量大于需求数量;再使用禁忌搜索找到最佳组合的任务集;。最后给任务分配教室输出课表[1]。
1 禁忌搜索算法介绍
禁忌搜索算法是一种启发式算法,可用于解决组合优化问题。禁忌搜索从模拟人的智力过程入手,在算法中引入记忆装置。算法从一个初始可行解出发,选择一系列的特定搜索方向作为试探,选择实现使目标函数值减少最多的移动。为了避免陷入局部最优解,禁忌搜索中采用了一种灵活的“记忆”技术,即对已经进行的优化过程进行记录和选择,指导下一步的搜索方向,这就是禁忌表的建立[2]。禁忌表中保存了最近若干次迭代过程中所实现的移动,凡是处于禁忌表中的移动,在当前迭代过程中是不允许实现的[3],这样可以避免算法重新访问在最近若干次迭代过程中已经访问过的解,从而防止了循环,帮助算法摆脱局部最优解[4]。另外,为了尽可能不错过产生最优解的移动,禁忌搜索还采用藐视准则的策略,当某个禁忌候选解的适配值优于“best so far”状态,则解禁此候选解为当前状态和新的“best so far”状态[5]。
2 禁忌搜索的排课模型
榆林学院的现状是,现有15个院系,全日制在校学生14869人,教职员工957人。学校现有普通教室128个,媒体教室46个,语音教室5个,排课任务繁重。根据排课人员的经验,考虑的问题主要有如下6条:
1)同一教师在同一时间只能安排一门课程;
2)同一班级在同一时间只能安排一门课程;
3)同一教室在同一时间只能安排一门课程[6];
4)教室容量大于班级人数,且教室类型符合课程要求;
5)权值较高的课程安排在上午,权值低的课程安排在下午;
6)每周上多次的课程,课程间隔应大于一天。
前4条为硬标准,后两条为软标准。根据实际情况,建立如下模型。
授课任务:TASK={task|task=(c,h,l,s,w),c∈C,h∈H,l∈L,s∈S,w>0)}表示c班级上h教室的l课程,教室类型为s,课时是w。TrType(c,h)表示h教师给c班级上课的教室类型
课表单元:CT={ct|ct=(C,h,l,t,r),c∈C,h∈H,l∈L,t∈T,r∈R},表示h教师给c班级上的l课程安排在t时间的r教室。排课问题的目标是找出一个从授课任务到教室时间的二元组的映射关系[7]:F:task∈TASK→(t,r)∈T×R该映射关系满足以下约束条件,且目标函数值是最优的[8]。

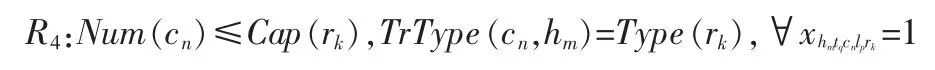
表示上课人数小于等于教室容量,且教室类型满足课程需要。
根据上述目标函数和约束条件,建立模型如下:
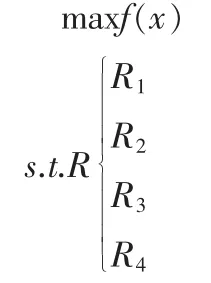
这里f(x)表示尽量满足的条件,且假定最优解能使得f (x)值最大。
3 禁忌搜索求解排课问题的算法实现
根据设计排课系统的需要,结合榆林学院的实际情况,排课系统的算法设计流程如图1所示[10]。

图1 排课工作流程
3.1输入任务集合
授课任务集合TASK={task|task=(c,h,l,s,w),c∈C,h∈H,l∈L,s∈S,w>0)}是预处理部分的输入;任务组集合GList= {Group}是预处理部分的输出,对其进行时间分配,实际是寻找一个从任务组集合到时间集合的一个映射;课表单元集合CT就是最终的输出结果[1]。
3.2分组预处理
分组预处理部分的解决采用基于网络流的预处理算法[11]。网络流G=(V,E)是一个有向图,其中每条边(V,E)均有一个非负的容量值,记为C=(U,V)≥0。如果(U,V)不包含E,则可以规定C=(U,V)=0。网络流中有两个特殊的顶点,即源点s和汇点t。
解决最大流问题,我们使用的是增广路算法。增广路算法是一种迭代算法[12],首先要对图中所有顶点对的流大小清零,此时的网络流大小也为0;在每次的迭代中,通过寻找一条“增广路径”来增加流的值[13]。增广路径可以看作是源点s到汇点t的一条路径,并且沿着这条路径可以增加更多的流,直至迭代无法再找到增广路径位置,此时必然从源点到汇点的所有路径中都至少有一条边的满边 (即边的流的大小等于边的容量大小)。分组预处理完成后,得到一个任务组集合GList,再对其进行时间分配[14],主要使用禁忌搜索算法进行最优化求解。
3.3基于禁忌搜索的时间分配算法
以随机方式产生初始解,如x*=(1,2,…,10,0,0,0,0)[15],f (x)表示目标函数值,禁忌表tabulist:=Φ;,最优解best_x:=Φ;
循环:
while结束条件不满足do
begin
1)生成x的邻域N(x)
2)生成候选解集:
从x的邻域N(x)中找出一定数量的解作为候选解集合openlist(x).
3)搜索:

4)禁忌表更新

算法运行结束,求得最优解。再基于贪心思想分配教室,最后就能得到周课表的分配方案。
3.4算法运行实例
如图2所示,是算法运行完毕,生成的课程查询页面的截图。
4 结束语
该系统符合教室分配的实际情况,可以方便的调整算法参数,使得排课结果更令人满意,且有较高的搜索效率。该排课系统已用于榆林学院数统院排课系统进行测试,实际应用表明该系统具有排课快捷方便、人机界面友好等特点,达到了设计要求。
[1]彭超.禁忌搜索求解排课问题的应用研究[D].西安电子科技大学,2007.
[2]王连山.关于遗传、蚁群、禁忌搜索算法的比较[J].电脑编程技巧与维护,2009(24)18-21.
[3]郭娜.基于节约算法和移动方向的禁忌搜索算法 [D].大连:大连理工大学,2009.
[4]李益华,林文南.一种改进的Tabu Search算法及其在区域电网无功优化中的应用 [J].电力科学与技术学报,2008 (2):60-65.
[5]刘光远,贺一,温万惠.禁忌搜索算法及其应用[M].北京:科学出版社,2014.
[6]王惠君,方明.浅析高校课程表的编排[J].中国科技信息,2010(11):273-274,284.
[7]陈小红,陈晓东.禁忌搜索算法解决赋权覆盖问题[J].价值工程,2011(26):89-91.
[8]刘长彬.基于遗传算法和禁忌搜索算法的排课系统研究[J].软件导刊,2014(10):68-70.
[9]周芬.遗传算法在多校区排课系统中的应用[J].科技信息,2010(6):234.
[10]张媛.基于J2EE的实验室排课系统的设计与实现[D].西安:西安电子科技大学,2010.
[11]赵礼峰,陶晓莉.最小费用最大流问题的一种新算法[J].计算机技术与发展,2014(1):130-132.
[12]马毅,严余松,户佐安.网络优化的最大利润问题及其增广路算法[J].计算机工程与应用,2015(1):1-4,80.
[13]王勤波.最小费用流问题及其扩展[D].青岛:青岛大学,2009.
[14]丁振国,赵红维.禁忌搜索求解排课问题的应用研究[J].微电子学与计算机,2008(4):27-29.
[15]邓志杰.基于图模型与遗传算法相结合的排课问题研究[J].信息技术,2014(1):146-149.
Design of course scheduling system based on Tabu Search
ZHANG Yuan,QI Lan
(School of Mathematics and Statistics,Yulin University,Yulin 719000,China)
In order to realize the automatic arrangement and improve the work efficiency of the university.The system is based on the method of network flow,which is divided into several groups.Then,the optimal solution of the time and task groups is found by using the tabu search algorithm.The practical application shows that the system has the characteristics of quick and easy use,and can meet the design requirements.
scheduling;grouping;tabu search;optimization
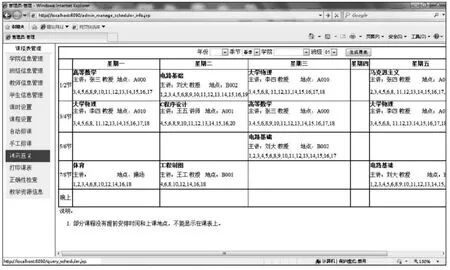
图2 课程查询页面截图
TN915.02-34;TP391
A
1674-6236(2016)22-0071-03
2015-11-23稿件编号:201511221
榆林学院青年科技基金(14yk33)
张 媛(1981—),女,陕西榆林人,硕士,讲师。研究方向:计算机及其应用、算法。
